1.4. Модели генерирования спроса на пассажирские перевозки

Модели генерирования поездок. Наиболее значительное изменение в модельном подходе к генерированию поездок произошло в начале 60-х годов, когда появились подходы, основанные на дезагрегации базовой (для моделей) информации о населении вплоть до данных о семьях или отдельных жителях. Эти подходы сменили обычные до тех пор приемы регрессионного анализа зональной статистики. Как настоятельно подчеркивают Флит и Робертсон [23], агрегирование спроса до зонального (или какого-то иного крупномасштабного) уровня влечет за собой заметную потерю информации и элеминирует значительную часть зависимостей, учет которых необходим в поведенческой модели пассажира. По этой причине зональные регрессии давали подозрительно хорошие результаты в статистическом смысле, но фактически устойчивость, а также прогностическая и объяснительная ценность этих ранних результатов были весьма невелики.

Гораздо более удовлетворительный подход к прогнозированию поездок и особенно тех, что связаны с местом жительства, был разработан Вуттоном и Пиком [67], которые в качестве основной учитываемой единицы по населению взяли семью. Коэффициенты подвижности были установлены для 108 категорий семей, различающихся числом автомобилей в их владении (три уровня), размером дохода (шесть уровней) и составом семьи (шесть уровней). Были разработаны модели прогнозирования численности семей по выделенным категориям. Аналогичный анализ был проведен для получения характеристик о назначении поездок, в связи с чем на основе официальной статистики были определены группы занятости и получены их количественные характеристики. Такой подход на дезагрегированной информации широко используется во многих работах начиная с середины 60-х годов.

Важное новшество появилось при исследовании транспортных проблем г. Ковентри [12], где впервые была использована модель генерирования поездок, основанная на данных непосредственно о жителях. В классификации жителей учитывались следующие характеристики: пол, возраст, занятость в производстве, владение легковым автомобилем и т. п. Семьи в то же время группировались по числу автомобилей в их владении (три уровня) и по размеру семейного дохода (четыре уровня). Полученные в итоге 104 группы в дальнейшем при рассмотрении конкретных целей значительно сокращаются в своем числе. Табл. 1.1 иллюстрирует использование различных методов расчета спроса на перевозки в нескольких исследовательских работах.

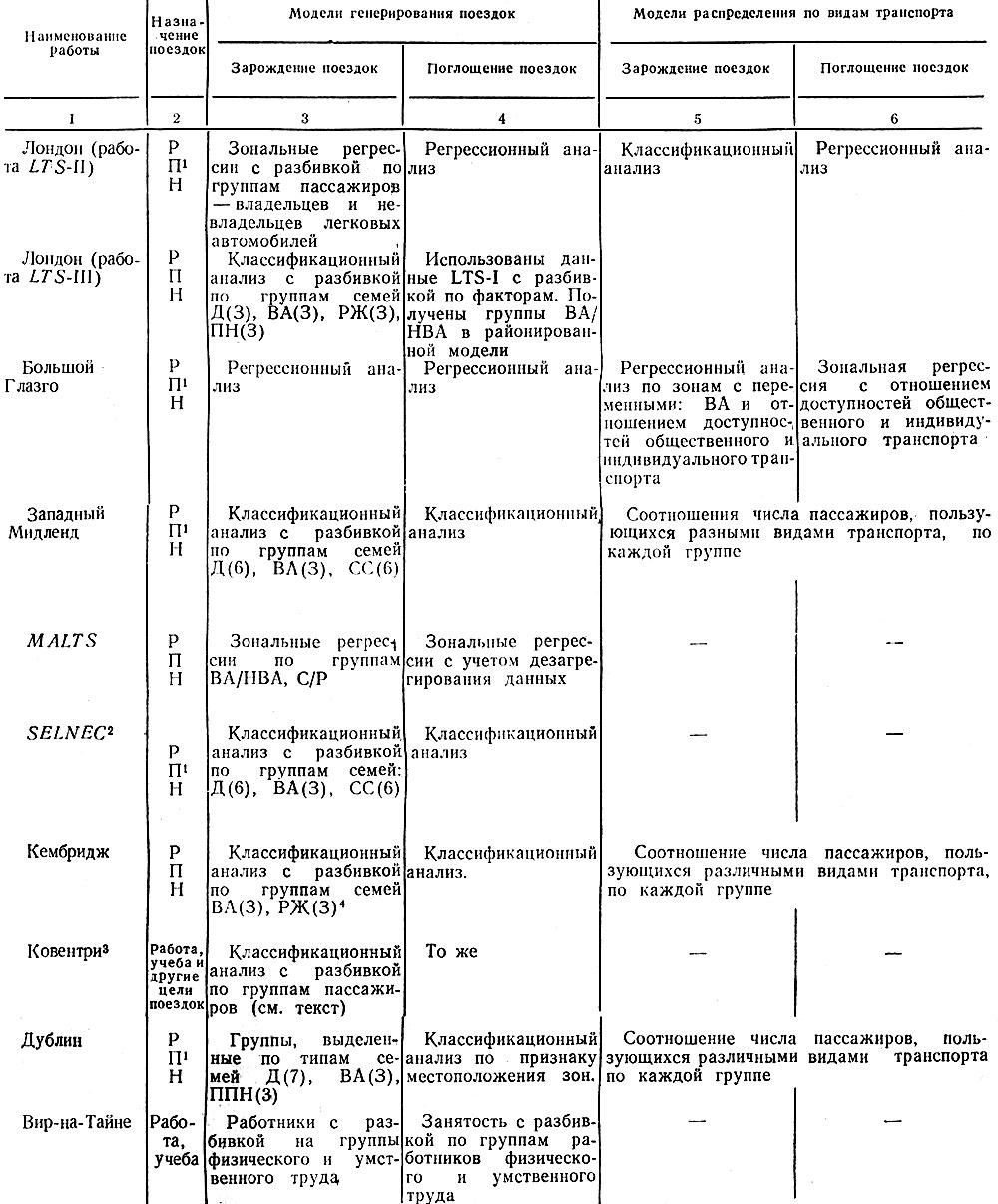
Таблица 1.1. Основные методы определения спроса на пассажирские перевозки

¹ (В модели выполнено дальнейшее дезагрегирование по целям поездок.)

² (South Eeast Lancashire North Eeast Cheshire (SELNEC) - работа [46], выполненная для графств Ланкашир и Чешир.)

³ (Использована специальная модель для пеших переходов.)

⁴ (В оригинале применено специальное обозначение LOC (3) для еще одного признака разбиения, но не дано расшифровки этого обозначения. Его значение не удалось также достаточно достоверно установить по тексту (прим. ред.).)

Примечания. Цель поездок (колонка 2): Р - деловые поездки из дома на работу и обратно; П - прочие поездки из дома и обратно; Н - поездки, не связанные с местом жительства.

Признаки выделения групп жителей с указанием (в скобках) числа выделяемых групп! Д (...) - доходность; ВА (...) - наличие автомобилей в личном пользовании; НВА - отсутствие автомобилей в личном пользовании; РЖ (...) - работающие; ПН (...) - плотность заселения; ОПН (...) - общая плотность населения; СС (...) - структура семьи; С/Р - служащие/рабочие.

Наличие в графе прочерка означает, что соответствующие колонке модели в данной работе не применялись.

Важным моментом в переходе от агрегированной зональной информации к более подробным региональным данным является возможность повышения одновременно и экономичности и эффективности работ при сборе и использовании данных. Значительная часть этого эффекта получается на этапе генерирования поездок. Получение данных о населении в необходимой для модели детальности является важным этапом в прогнозировании спроса на перевозки. В практике регионального планирования в Англии было принято отделять вопросы накопления статистики об использовании городской территории от транспортных проблем. В большинстве случаев на уровне городских районов и даже зон данные для планирования получаются в процессе особого взаимодействия с плановыми органами. Рост доходов и (в последнее время) так называемого "дохода для покупки автомобиля" обычно дается в сумме за период планирования в то время, как прогнозы относительно численности индивидуальных автомобилей либо базируются на предложенном Таннером [51] методе экстраполяции, либо непосредственно включаются в процедуру моделирования группового состава населения.

Модели распределения поездок. С конца 50-х годов появилось много подходов к моделированию распределения поездок по направлениям: методы факторного роста, модели "использованных возможностей", гравитационные модели. Для вычисления поездок внутри рассматриваемого региона широко используется лишь последний из вышеназванных подходов, в настоящее время представленный видом, предложенным Вильсоном [65]. Гравитационная модель с двумя ограничениями, имеющая следующий общий вид:

T_ij = k_ij O_i D_j A_i B_j F(c_ij), (1.1)

традиционно использовалась для определения многих видов поездок и особенно поездок на работу. Балансирующие множители А_i и B_j вводятся с таким расчетом, чтобы матрица корреспонденции Т_ij согласовывалась с независимыми прогнозами величин отправлений О_i и прибытий D_j, получаемых по зонам моделью генерирования поездок.

В моделировании распределения поездок по направлениям явно наблюдаются две тенденции. Во-первых, широко используются функции предпочтения F (c_ij), аналитическое выражение которых обычно задается таким видом:

F(c_ij) ≈ ехр( - βс_ij).

Эти функции используются в дополнение к эмпирическим функциям, полученным из данных о распределении поездок по дальности. С другой стороны, еще более широко используются композиционные функции для выражения стоимости проезда с_ij через стоимости проезда на различных видах транспорта с^k_ij. В тех ранних исследованиях, в которых распределение по видам транспорта производилось после распределения по направлениям, принятие того допущения, что людям почти безразличен вид транспорта, приводило к загрузке магистральных дорог. В этом воплотилась та принципиальная непоследовательность такого подхода, что региональное решение людей (о направлении поездок), которые предпочли общественный транспорт, было предопределено характеристиками по существу не выбираемого вида транспорта. С другой стороны, изменения в уровне обслуживания в системе общественного транспорта не влияли на распределение тех пассажиров, которые свободно выбирают вид транспорта.

Использование в некоторых работах констант k_ij для избранного числа пар зон представляет, вероятно, наиболее яркую иллюстрацию дилеммы, стоящей перед методом факторных срезов: либо терпеть в "разрезе" значительное несовпадение модельных прогнозов с наблюдаемыми, либо принимать непроверенные гипотезы представления сложных явлений (в данном случае гипотезы пространственного распределения, поездок). Методы распределения пассажиропотоков, используемые в моделировании индивидуальных поездок, даны в табл. 1.2.

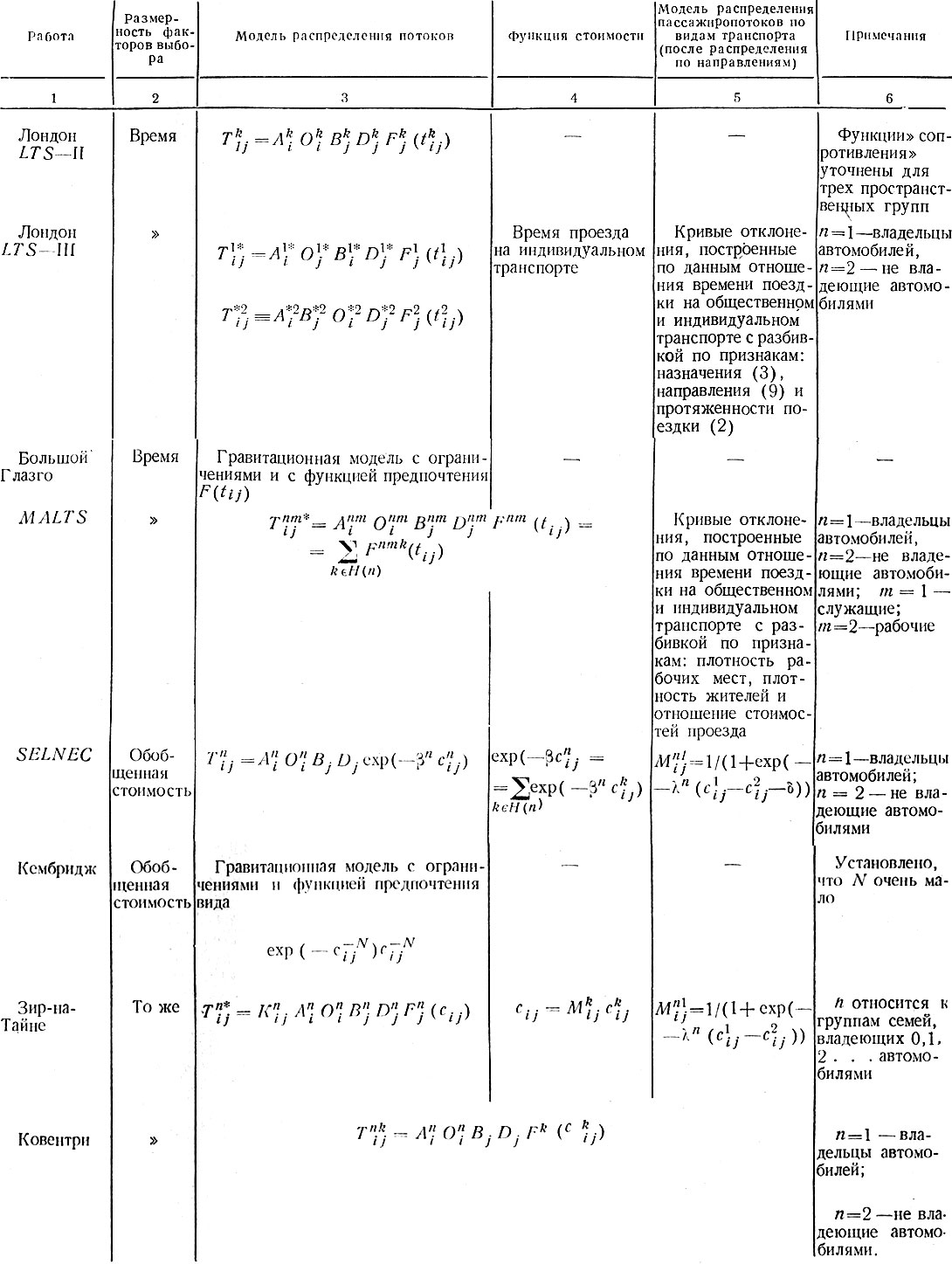
Таблица 1.2. Модели распределения пассажиропотоков по маршрутам и видам транспорта

Примечание. Здесь и в других местах книги наличие знака ^* вместо индекса означает, что величина представляет собой сумму по всем допустимым значениям соответствующего индекса (прим. ред.).

Наложение пассажиропотоков. Методы наложения потоков можно классифицировать несколькими способами, но, возможно, наиболее подходящей является классификация, основанная, во-первых, на том, что отражается момент выбора маршрута (имеют ли выбираемые между зонами маршруты одинаковую стоимость или существует, по мнению исследователя, разница в стоимостях проезда по этим маршрутам) и, во-вторых, учитывается или нет эффект загрузки маршрута при его выборе. "Многомаршрутность" поездок может явиться следствием либо разницы в стоимостях поездок по маршрутам, либо разницы в пропускной способности, возникающей после работы процедур пересчета пропускной способности.

В ряде ранних работ потоки накладывались без учета ограничений пропускной способности и таким образом межзональные поездки ложились на единственный путь между каждой парой зон. Иногда существовала возможность немодельного уточнения скоростей на звеньях и переназначения нагрузок во избежание значительных несоответствий между начальными и результативными временами проезда по звеньям. С середины 60-х годов в большей части работ используется один из эвристических методов наложения потоков: или итеративный, или последовательного (пошагового) приращения нагрузки. Эти методы работают, обеспечивая равновесие в сети по первому критерию Уолдропа [59]. При их использовании подразумевается единообразие поведения пассажиров, выбирающих маршруты передвижения. В настоящее время имеется несколько методов, снимающих жесткость этого условия и учитывающих разнообразие в поведении населения. Видное место среди них занимают методы Р. Дайела [18] и Д. Беррела [10]. Первый из них использовался в программе наложения потоков UROAD [53], в то время как подход Д. Беррела, связывающий с каждым ребром некоторое распределение стоимостей проезда, был принят в ряде работ в Англии. Два разработанных Д. Беррелом альтернативных подхода базируются на разных процедурах построения дерева путей и оценки маршрутов. В многомаршрутном варианте фрагменты матрицы поездок накапливаются на деревья путей, построенные для каждого фрагмента при различных оценках времени передвижения по звеньям. Во втором варианте используется, строго говоря, принцип "все или ничего", допускающий различные маршруты передвижения между источником и стоком в промежуточных узлах сети, причем строится одно дерево из каждой зоны при раздельных оценках времени передвижения по звеньям. Последний из вышеупомянутых методов часто использовался вместе с методами ограничения пропускной способности. Было показано, что при этом улучшается сходимость в итеративных процедурах наложения потоков. Подробный обзор таких моделей приводится в [55].

Пока еще ни в одной работе не использовались алгоритмы, основанные на принципах математического программирования, которые бы давали сходимость к равновесию, удовлетворяющему принципу Уолдропа. Эвристические методы гарантии такой сходимости не обеспечивают. Рейтер [44] описывает алгоритм возможных направлений, предложенный в составе пакета UPTS.

Процедуры наложения потоков для общественного транспорта обычно разрабатывались на базе принципа "все или ничего" без специального учета условий проезда для разных систем общественного транспорта. Так, например, программа наложения потоков HUD допускает распределение нагрузки между параллельными маршрутами различных видов транспорта; в то же время существуют более тонкие приемы многомаршрутного моделирования, использованные, например, в [14] и [15]. В табл. 1.3 перечислены методы наложения потоков, использовавшиеся в нескольких исследованиях, проводившихся в Англии.

Таблица 1.3. Методы наложения потоков и их использование

Модели распределения пассажиропотоков по видам транспорта. Ни в одном другом элементе транспортной модели не обнаруживается такого множества разнообразных подходов, как это имеет место в моделировании распределения пассажиропотоков по видам транспорта. Переменные, используемые для прогнозирования роли того или иного вида транспорта, существенно различаются в зависимости от тех связей, которые учитываются в модели распределения. Это собственно и отражает разные допущения о структуре функций полезности, связанных с принятием решений о выборе конкретного вида транспорта и о географии поездок.

Обозначения;

Оценки стоимости проезда; Т - время; ОС - обобщенная стоимость (сочетание затрат времени и денег).

Методы наложения и их характеристики: ВиН - наложение по принципу "все или ничего" без ограничения пропускной способности; ИТН - итеративное наложение с использованием принципа "все или ничего"; ПН - последовательное порционное наложение потоков: ПЛН - наложение пошаговыми приращениями; МПН - раздельное наложение потоков; ММН - многомаршрутное наложение.

Во-первых, отметим модели, использование которых предшествует распределению пассажиропотоков по направлениям. Существенным для них является выделение социально-экономических характеристик населения, в частности уровня владения автомобилями, что считается определяющим в выборе вида транспорта для поездок. В них также представлено влияние уровня обслуживания на транспорте, выражаемое с помощью агрегированных мер доступности (как это, например, сделано при исследовании транспортных проблем Большого Глазго или Лондона [27]). Особенно распространенными стали модели, базирующиеся на семейных характеристиках. В них соотношение потоков по видам транспорта определяется для каждой группы семей. Во многих использующихся по настоящий день методиках, разработанных без учета уровня обслуживания, необоснованно предполагается, что любые изменения в сети влекут соответствующие изменения в сферах влияния того или иного вида транспорта. Такие модели не только нереалистичны, но и нечувствительны к изменениям в стоимости проезда в системах общественного и индивидуального транспорта.

Во-вторых, отметим модели одновременного распределения пассажиропотоков по маршрутам и видам транспорта. Несмотря на то, что предложения о разработке методов, одновременного распределения пассажиропотоков по маршрутам и видам транспорта выдвигались уже в начале 60-х годов и легли в основу целого ряда эконометрических моделей спроса на междугородные пассажирские перевозки в США, они мало использовались в исследованиях городского транспорта, проводившихся в Англии. Вообще говоря, в них использовались известные методы энтропийной максимизации. Общий вид модели, применявшейся в г. Ковентри [12] и предложенной для исследования транспорта в Большом Лондоне [28], приводится ниже:

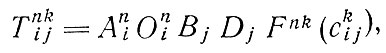
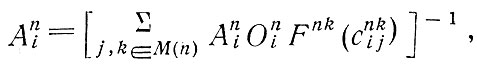
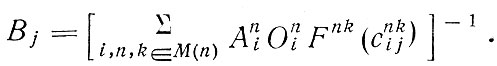
Здесь только один параметр (функция F) отражает распределение, связанное с выбором вида транспорта и направления поездок.

В-третьих, отметим модели распределения по видам транспорта, применяемые после распределения потоков по маршрутам. Один из наиболее распространенных в середине 60-х годов приемов распределения пассажиропотоков по видам транспорта предусматривал использование специальных кривых переключения. Потоки поездок классифицировались по нескольким признакам, один из которых был непрерывной переменной, представляющей относительную или абсолютную разницу в стоимости или времени поездок. В принципе метод сводился к процедуре подсчета и просмотра пропорций для разных видов транспорта раздельно по категориям поездок. В отличие от этого метода, основанного на использовании эмпирических кривых, Вильсоном [64] предложены аналитические выражения, обычно включающие логические зависимости, а также дезагрегированные данные [42]. Эти методы наиболее широко применяются сейчас в Англии, и для решения дилеммы выбора в агрегированной форме используют выражение

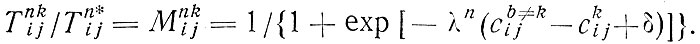
Для калибровки зависимости этого вида требуется определение параметров λ и δ. В работе [46], где данная форма была использована впервые, индекс n выделял группы семей, владеющих и не владеющих автомобилями, а значения параметров обобщенной стоимости заимствовались из работы Д. Квормби [40]. Позднее (например, в исследовании транспортных проблем г. Ноттингем и в районе Шеффилд-Ротерхэм) использовалось разбиение на три группы по признаку владения легковыми автомобилями, что позволило лучше учесть обстоятельства выбора вида транспорта.