2.2. Сети, построение деревьев кратчайших путей и матриц стоимостей

Описания сети. Как и многие другие транспортные модели, наша модель рассчитана на две сети: индивидуального и общественного транспорта. Эти сети вводятся на вход двух основных блоков модели: процедуры построения дерева путей минимальной стоимости, с помощью которой вычисляются матрицы стоимостей, а также блока наложения потоков, где одновременно моделируются последствия этого наложения в виде матриц стоимостей, вводимых в модель распределения пассажиропотоков по маршрутам и видам транспорта. Модели транспортных сетей были построены по данным, о которых будет рассказано ниже в разделе 2.3. В обеих сетях имеются ребра двух видов: "реальные" и "фиктивные". В сети индивидуального транспорта реальные ребра представляют определенным образом направленные дороги либо некий путь. Таким образом, дорога с односторонним движением может быть представлена направленным ребром (дугой) графа, имеющим разрешенное направление движения. Дорога с двусторонним движением состоит из двух направленных ребер (дуг), по которым движение осуществляется в противоположных направлениях.

С каждым реальным ребром сети индивидуального транспорта связаны: один из десяти кодов групповой принадлежности, указывающий на пропускную способность ребра (например, шоссе или улица с двусторонним движением); длина ребра; время проезда по ребру, определенное по данным наблюдений.

Фиктивные направленные ребра в сетях индивидуального транспорта соединяют сеть с центрами зон (точками, выделяемыми в каждой зоне, с которыми принято соотносить начало и конец поездки, причем зоны соответствуют делению рассматриваемого графства Западный Йоркшир на небольшие районы). С каждым фиктивным ребром связаны: его длина; время, необходимое на передвижение по ребру согласно имеющимся оценкам; величина штрафа (в основном это время, затрачиваемое на поиск стоянки для автомобиля, его постановку и на выезд со стоянки).

В сети общественного транспорта реальное ребро представляет определенно направленный маршрут общественного транспорта. С каждым из них связаны его длина и время на передвижение по ребру. В этом случае фиктивные ребра также символизируют доступ к местам соединения реальных ребер сети. С каждым фиктивным ребром в этом случае связаны время подхода и отхода и время ожидания транспорта.

В той и другой сети ребра соотнесены с вершинами, обозначающими начало и окончание ребра. Таким образом, список ребер дает полное топологическое описание сети.

Построение дерева путей минимальной стоимости. Пути минимальной стоимости из центра какой-либо зоны к центрам остальных зон образуют дерево минимальных путей, и термин "построение дерева" обозначает процесс, при помощи которого определяются такие пути на описанных сетях. При этом используются коэффициенты для определения обобщенной стоимости проезда по звеньям сети. Матрицы (которые будут рассматриваться в разделе 2.2.3), а также пути минимальной стоимости используются в моделях наложение потоков, описываемых в разделе 2.5.

Как указано в [38], задача определения пути минимальной стоимости сводится к решению уравнений динамического программирования Беллмана [3]:

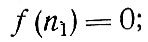
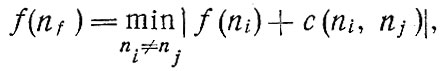
где n_i, n_j - вершины сети; c(n_i, n_j) - положительная функция стоимости проезда по ребру.

На этом принципе основано несколько общеизвестных методов вычисления кратчайших путей на сети. В то же время, при построении путей минимальной стоимости для сети общественного транспорта пришлось существенно изменить этот традиционный подход, поскольку здесь для определения путей минимальной стоимости проезда мы обязаны учесть кусочно линейную функцию платы за проезд. Такого рода функция могла бы включаться в процесс построения дерева оптимальных путей с помощью "поисковых" таблиц, в которых приводятся величины платы за проезд по каждому, маршруту на средствах общественного транспорта. Данный метод был отвергнут на том основании, что он требует больших объемов машинной памяти, а также потому, что авторы хотели проверить влияние изменений в функции платы за проезд. Для этого эксперимента потребовалось бы очень много машинного времени на обновление "поисковых" таблиц. Поэтому мы разработали и запрограммировали новый алгоритм построения дерева минимальных путей [6], пригодный для использования нелинейной функции платы за проезд без применения таблиц. Для таких функций стоимости принципиально важным является некорректность сформулированного Беллманом принципа оптимальности, заложенного в уравнениях (2.1) и (2.2). Поэтому для выбранной сети алгоритм Дийкстра использовать нельзя.

Новый алгоритм построения дерева путей минимальной стоимости для общественного транспорта "запоминает" варианты маршрутов в каждую вершину, встречающуюся в процессе просмотра путей из вершины отправления и "отказывается" от этих путей лишь тогда, когда они в принципе не могут войти в состав минимального пути независимо от того, где находится вершина, представляющая пункт назначения. Вообще говоря, выбор путей зависит от природы принятой нами функции платы за проезд.

Для построения кратчайших путей в сети индивидуального транспорта используется метод Десоло [37].

Стоимости межзональных поездок. Матрицы стоимости межзональных поездок получаются с помощью алгоритмов построения кратчайших путей, упомянутых выше и так, как это рекомендовано в проекте [45, 46].

Стоимость межзональных поездок определяется по формуле

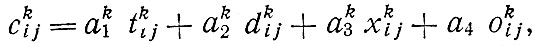
где 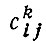- определяется как обобщенная стоимость передвижения из зоны i в зону j на транспортном средстве типа k (k=1 или 2 и обозначает использование индивидуального или общественного транспорта соответственно);

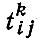  - время проезда между пунктами i и j на транспортном средстве типа k, выраженное в единицах времени;

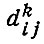  - расстояние проезда между пунктами i и j на транспортном средстве вида k по минимальному пути, выраженное в единицах расстояния;

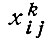  - дополнительное время (в единицах времени) ожидания, подхода-отхода и переезда, затрачиваемое при переезде между пунктами i и j на транспортном средстве вида k;

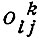  - дополнительные затраты (в частности, плата за стоянку автомобиля), связанные с поездкой на транспортном средстве вида к между пунктами i и j (применимо только по отношению к индивидуальному транспорту); а^k₁ и a^k₃ - коэффициенты, отражающие оценки соответственно времени пребывания в транспортных средствах и вне их; а^k₂ - оценка величины эксплуатационных расходов в расчете на единицу расстояния проезда на средствах индивидуального транспорта. В расчетах, выполняемых для общественного транспорта, d^k_ij (второй член правой части равенства 2.3) заменяется функцией платы за проезд. В практических расчетах величины обобщенной стоимости преобразованы в обобщенные единицы времени делением величин C^k_ij из формулы (2.3) на величину оценки времени а^k₁.

Стоимости внутризональных поездок. Стоимости, стоящие на диагонали матрицы стоимостей, вычисляются особым образом. Поездки, начинающиеся и заканчивающиеся в одной зоне (предусмотренные при моделировании транспортного обслуживания крупных зон), составляют около 30% всех поездок. Такая большая доля внутризональных поездок требует от нас не только учета поездок данного типа, но и крайне тщательной оценки таких поездок, вследствие чего эта оценка выполняется в рамках модели распределения пассажиропотоков по направлениям. В то же время, производилась отдельная оценка стоимости внутризональных поездок, поскольку описанные процедуры построения дерева путей минимальной стоимости не дают сведений о стоимости внутризональных поездок и характеризуют только межзональную сеть. Стоимости внутризональных поездок вводятся в матрицу стоимостей межзональных поездок, что позволяет составить полную матрицу стоимостей поездок на зональном уровне. Стоимости внутризональных поездок вычислялись следующим образом:

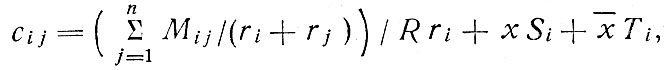
где 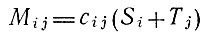- стоимость передвижения; с_ij - полная стоимость передвижения из зоны i в соседнюю зону j; r_i - радиус зоны i (площадь зоны i); n - число зон, соседних с зоной i; S_i - "начальная" стоимость в зоне i; T_j - "конечная" стоимость в зоне j; R, х, х^- - коэффициенты.

Вышеприведенная формула получена в работе [5], Она основана на геометрических соображениях, когда используется несложное, но весьма эффективное преобразование поверхности реальных неизотропных стоимостей в двухмерную плоскость, позволяющую пользоваться соответствующими геометрическими приемами с учетом образования поездок в окрестности зоны для оценки стоимостей внутризональных поездок.