2.2.1. Неподвижное колесо

Пневматическая шина, смонтированная на обод и накаченная воздухом, изменяет свои размеры по сравнению с исходной конфигурацией, определяемой пресс-формой, в которой покрышка проходит заключительную стадию формирования. Как правило, автомобильные шины при накачивании воздухом увеличивают свои размеры по диаметру. Это приводит к растяжению каркаса и протектора по беговой дорожке шины.

При нагружении автомобильного колеса нормальной нагрузкой шина подвергается деформации и в зоне контакта с опорной поверхностью получает нормальный прогиб. На рис. 2.6 схематично показано неподвижное автомобильное колесо, находящееся под воздействием одной нормальной нагрузки. Контакт шины с опорной поверхностью характеризуется при этом следующими параметрами:

нормальным прогибом шины h₂ = r_св - r_ст, где r_св - свободный и r_ст - статический радиусы колеса;

длиной контакта l_к;

углом контакта α_к, складывающегося из двух равных между собой углов α₁ и α₂;

площадью контакта F, которая для большинства современных шин при полной нормальной нагрузке имеет форму, близкую к прямоугольной с осями l_к и b.

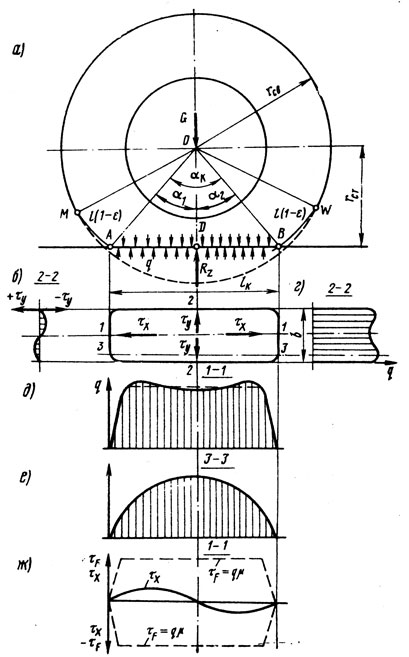
Рис 2.6. Схема сил, действующих на неподвижное колесо и эпюры распределения контактных напряжений по площади контакта

При воздействии на колесо нормальной нагрузки G сумма нормальных контактных напряжений q по площади контакта равна нормальной нагрузке, т. е.

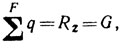
где R₂ - нормальная реакция опорной поверхности.

Нормальные контактные напряжения q распределяются неравномерно по площади контакта шины. При малых прогибах шины нормальные напряжения должны быть пропорциональными нормальной деформации шины в данной точке поверхности контакта. Поэтому нормальные напряжения должны увеличиваться от начала контакта в точке А к его центру. В точке D они должны достигнуть максимальной величины. В направлении от точки D к В напряжения будут снова снижаться симметрично распределению на участке DA и пропорционально уменьшению нормальной деформации шины в данных радиальных сечениях. При В малых прогибах шины распределение нормальных напряжений по длине контакта должно подчиняться некоторым эллиптическим или параболическим зависимостям, как показано на рис. 2.7.

С увеличением нормального прогиба шины возникает новое явление, влияющее на характер распределения нормальных напряжений по длине контакта. При больших нормальных прогибах беговая дорожка шины в результате изгибного эффекта стремится в центре контакта переместиться внутрь контакта, т. е. отжаться от опорной поверхности.

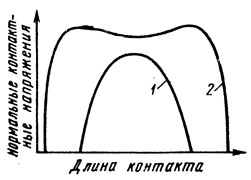
Рис. 2.7. Распределение нормальных контактных напряжений по длине контакта шины при малых (1) и больших (2) нормальных прогибах

Поворот беговой дорожки происходит относительно поверхностей контакта, лежащих в зоне точек А и В (см. рис. 2.6).

В связи в этим нормальные контактные напряжения в центре контакта (в зоне точки D) должны уменьшаться, а в зонах начала контакта (точки А и В) повышаться. В результате при больших прогибах шины эпюры распределения нормальных напряжений по длине контакта шины должны приобрести другую форму, чем при малых прогибах. В этом случае эпюры приближаются к трапецеидальной форме.

По ширине контакта из-за неодинаковой радиальной жесткости беговой дорожки в разных продольных сечениях, нормальные напряжения распределяются также неравномерно. Беговая дорожка шины имеет наименьшую толщину в центральной части беговой дорожки и существенно большую в своих плечевых зонах (по углам беговой дорожки). Таким образом, в центральной части беговая дорожка имеет меньшие радиальную и изгибную жесткости, а в плечевых зонах - большие. В соответствии с этим упомянутый выше изгибной эффект беговой дорожки будет проявляться в большей степени в центральной зоне и в меньшей степени в плечевых зонах. Поэтому и при больших прогибах шины эпюры распределения нормальных напряжений по длине контакта в плечевых зонах должны в большей степени подчиняться эллиптическим или параболическим зависимостям, чем трапецеидальным. Нормальные напряжения в этих зонах должны быть большими по абсолютным значениям, чем в центральной части беговой дорожки.

На рис. 2.6, д показана эпюра распределения нормальных напряжений q по длине контакта в центральной части беговой дорожки (сечение 1-1), приближающаяся к трапецеидальной форме и соответствующая нагружению шины с большими прогибами при полной нормальной нагрузке на колесо. Верхнее основание трапеции, приближенно отражающей эпюру, показано штрихами.

Эпюра распределения нормальных напряжений для сечения 3-3, лежащего в плечевой зоне беговой дорожки, показана на рис. 2.6, е. Она представляет собой некоторую параболическую зависимость. На рис. 2.6, г представлена эпюра распределения нормальных напряжений по ширине контакта в сечении 2-2.

Описанная качественная картина закономерностей распределения нормальных контактных напряжений по площади контакта автомобильной шины подтверждается экспериментальными исследованиями, посвященными измерению напряжений в контакте шины [7].

На рис. 2.6, а в зоне контакта шины пунктиром показан первоначальный контур шины по наружному диаметру. В зоне контакта внешние силы, приложенные к шине со стороны дороги, уравновешивают нагрузку от внутреннего давления воздуха. Вследствие этого в определенной зоне OMADBW беговая дорожка сокращается по длине. В зонах МА и BW элемент беговой дорожки, первоначально имеющий длину l, сокращается по длине до l (l-ε), где ε - относительная окружная деформация беговой дорожки. Непосредственно в зоне контакта - зона ADB - элементы беговой дорожки, наряду со стремлением сжаться в окружном направлении, при выпрямлении беговой дорожки получают угловое смещение относительно обода колеса: влево в зоне угла α₁ и вправо в зоне угла α₂. Точка D в этом случае является нейтральной - она не имеет углового смещения относительно обода. Смещенные элементы беговой дорожки стремятся сдвинуться относительно опорной поверхности к поперечной плоскости колеса. Однако их смещению препятствуют силы трения, действующие между шиной и опорной поверхностью. В результате этого возникают продольные касательные напряжения τ_х, приложенные к шине в направлении от центральной поперечной плоскости к краям контакта (к зонам точек А и В).

Эпюры распределения сил трения τ_F, если принять коэффициент трения μ постоянным по всей площади контакта, т. е. не зависящим от величины нормальных напряжений, подчиняются тем же закономерностям, что и нормальные контактные напряжения q, рассмотренные выше. На рис. 2.6 штрихами показаны эпюры распределения по длине контакта сил трения τ_F = qμ в центральной части беговой дорожки.

Напряжения равны нулю в начале контакта (точки А и В), где силы трения равны нулю, и на центральной поперечной плоскости (точка D) как нейтральной плоскости, в зоне которой изменяется направление действия продольных касательных напряжений.

От точки D к точкам А и В напряжения τ_x возрастают в соответствии с изменением углов смещения элементов беговой дорожки относительно обода колеса, достигая максимальной величины между точками D и A, D и В. Таким образом, эпюра продольных касательных контактных напряжений τ_х по длине контакта должна иметь вид, показанный на рис. 2.6, ж.

Продольные касательные напряжения τ_х для неподвижного колеса, нагруженного одной нормальной нагрузкой, могут быть приближенно выражены следующей синусоидальной зависимостью:

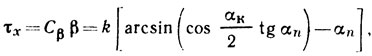
где C_β - коэффициент крутильной жесткости шины; β - угол закрутки, т. е. угловая деформация (смещение) элементов беговой дорожки относительно обода при нормальном прогибе шины; α_к - угол контакта шины; α_n - текущее значение угла поворота колеса (начало отсчета от вертикали, проходящей через ось колеса).

В поперечном направлении по площади контакта с опорной поверхностью действуют поперечные касательные напряжения τ_у, природа которых аналогична природе продольных касательных напряжений τ_х, рассмотренной выше. Эпюра распределения поперечных контактных напряжений τ_у представлена на рис. 2.6, б.