2.2.2. Ведомое колесо

Схема сил, действующих на ведомое колесо и эпюры распределения контактных напряжений по длине контакта, показаны на рис. 2.8. Качение ведомого колеса происходит под действием толкающей силы Р_в, приложенной к оси колеса в горизонтальной плоскости, равной силе сопротивления качению ведомого колеса. При этом ось колеса перемещается справа со скоростью υ, а обод колеса вращается с угловой скоростью ω.

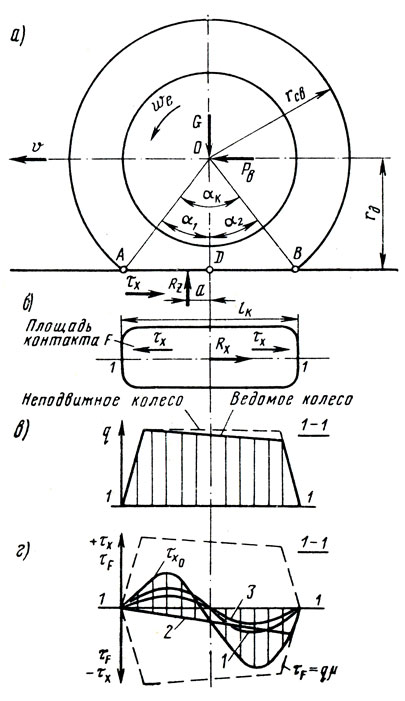
Рис. 2.8. Схема сил, действующих на ведомое колесо и эпюры распределения контактных напряжений по длине контакта

При качении автомобильного колеса его шина непрерывно деформируется в зоне контакта. В зоне первой половины угла контакта, в зоне угла α₁, шина прогибается и получает нормальный прогиб, а во второй половине угла контакта в зоне угла ₂ она выпрямляется и постепенно освобождается от прогиба, восстанавливая свою первоначальную форму.

На участке AD контакта к шине со стороны опорной поверхности прикладывается нормальная реакция, которая противодействует вращению колеса, т. е. создает момент, препятствующий вращению колеса. На участке DB нормальная реакция опорной поверхности отталкивает шину от опорной поверхности, т. е. создает момент, способствующий качению колеса. В связи с наличием гистерезисных потерь в материале шины давление беговой дорожки на опорную поверхность в зоне угла α₂ на участке контакта DB меньше, чем в зоне угла α₁ Поэтому нормальная реакция дороги на участке AD больше, чем на участке DB. Это приводит к тому, что общая реакция дороги смещается в направлений большей составляющей, т. е. в зону угла α₁ и точка приложения общей реакции смещается по направлению движения колеса на величину а относительно вертикали, проходящей через ось колеса.

В плоскости контакта ведомого колеса действует продольная касательная сила R_x, направленная против движения колеса. Сила R_x является результирующей продольных контактных касательных напряжений τ_х, приложенных к шине в контакте.

Уравнения равновесия сил и моментов, приложенных к ведомому колесу, дают соотношения:

R_z=G; R_x=P_в; P_вr_д=G_a.

В связи с описанным процессом деформации шины в контакте при качении эпюра нормальных контактных напряжений ведомого колеса несколько отличается от таковой для неподвижного колеса. Вследствие ослабления давления в зоне угла α₂ верхнее основание эпюры нормальных напряжений получает наклон в сторону выхода из контакта (см. рис. 2.8, в).

Картина распределения продольных контактных касательных напряжений шины ведомого колеса имеет свои особенности по сравнению с тем, что имеется у неподвижного колеса. При качении ведомого колеса возникают дополнительные составляющие продольных касательных сил, обусловленные действием в контакте продольной касательной силы R_x и дополнительным угловым смещением элементов беговой дорожки относительно обода колеса при проходе ими зоны контакта.

Как будет показано более подробно ниже (см. разд. "Ведущее колесо"), внешняя касательная сила, действующая в контакте эластичной шины, распределяется по длине контакта по треугольной зависимости, возрастая от нуля на входе в контакт до максимальной величины на выходе из контакта.

На рис. 2.8, г показаны эпюра 1 продольных касательных напряжений неподвижного колеса, а треугольная эпюра 2 представляет распределение по длине контактных напряжений τ_F, вызванных действием реакции дороги R_x, равной силе сопротивления качению ведомого колеса.

Беговая дорожка шины при равномерном качении ведомого колеса благодаря наличию значительного нормального прогиба шины в контакте проходит зону контакта с переменной угловой скоростью ω_n. Эта угловая скорость, как показано в работе [26], может быть выражена зависимостью

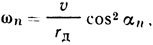
где υ - линейная скорость оси колеса.

В этой же работе приведена зависимость для определения угловой скорости обода колеса

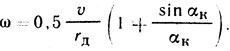
Анализ этих зависимостей показывает, что в зоне угла α₁ контакта в начале ω_n<ω, следовательно, по мере вращения имеет место нарастающее угловое отставание элементов беговой дорожки от обода колеса. Затем наступает момент, когда ω_n= ω, при котором нарастание углового смещения прекращается. После этого беговая дорожка вращается быстрее, чем обод колеса - ω_n>ω, что означает уменьшение углового смещения элементов беговой дорожки относительно обода колеса. В середине контакта (точка D) ω_n достигает максимальной величины, и угловое смещение элементов беговой дорожки полностью снимается, становится равным нулю.

В зоне угла α₂ наблюдается обратная картина. После прохода точки D угловая скорость ω_n начинает уменьшаться. Однако в начале угла α₂ элементы беговой дорожки шины вращаются быстрее, чем обод колеса, и они опережают вращение обода, получая угловое смещение по направлению вращения. Это смещение увеличивается до определенного предела. При равенстве ω_n=ω увеличение углового смещения прекращается. В зоне выхода из контакта снова ω_n<ω, угловое смещение уменьшается и на выходе из контакта становится равным нулю.

Мы видим, что характер рассматриваемых угловых смещений элементов беговой дорожки относительно обода колеса качественно аналогичен угловым смещениям, возникающим при нормальном прогибе шины, рассмотренным на неподвижном колесе. Таким образом, угловые смещения беговой дорожки, вызванные двумя различными причинами, совпадают по знаку и должны складываться.

Угловое смещение β, вызванное неравномерностью вращения беговой дорожки шины в зоне контакта, может быть определено по уравнениям (2.2 и 2.3).

Приближенное выражение для определения β имеет вид:

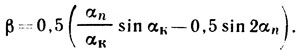
Продольные касательные напряжения пропорциональны углу, т. е.

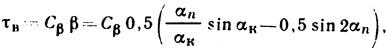
где С_β - имеет то же значение, что и в уравнении (2.1).

Эпюра изменения τ_в по длине контакта в соответствии с последним уравнением представлена на рис. 2.8, г синусоидальной кривой 3.

Общие продольные контактные касательные напряжения ведомого колеса τ_х.о представляют сумму указанных выше трех составляющих:τ_n, τ_F и τ_в.

На рис. 2.8, г видно, что эпюра продольных касательных напряжений ведомого колеса ассиметрична по длине контакта. Напряжения в зоне угла α₁ меньше, чем в зоне угла α₂. Касательные напряжения концентрируются во второй половине угла контакта, ближе к выходу из контакта.

Это обусловлено тем, что напряжения, вызванные внешней касательной силой, действующей в контакте, вычитаются в зоне угла α₁ и суммируются в зоне угла α₂. Это означает, имея в виду симметричность эпюр напряжений τ_n и τ_в по длине контакта, что разница между результирующими положительных и отрицательных касательных напряжений должна быть равна внешней касательной силе, действующей в контакте, т. е. силе сопротивления качению ведомого колеса.

На этом же рисунке штриховыми линиями показаны эпюры сил трения по длине контакта. В тех местах, где продольные касательные напряжения равны силам трения, наступает скольжение элементов беговой дорожки относительно опорной поверхности.

На входе в контакт и выходе из него должно иметь место скольжение. Очевидно, в связи с большой концентрацией касательных напряжений на выходе из контакта скольжение в этой зоне должно быть больше, чем на входе в контакт.

Описанная картина проскальзывания шины в условиях качения ведомого колеса подтверждается экспериментально [22].

Скольжение шины в контакте должно усиливаться с увеличением внешней касательной силы, действующей в контакте шины с дорогой. Этот вопрос нами будет рассмотрен ниже при анализе качения ведущего и тормозящего колес.

При прямолинейном качении автомобильного колеса характер распределения поперечных контактных касательных напряжений остается таким же, как и у неподвижного колеса. Поэтому в дальнейшем эти напряжения нами не рассматриваются.