4.3. Принятие проектных решений на основе прогнозной информации

Прогнозирование и нормирование показателей надежности деталей и агрегатов - один из этапов принятия проектных решений (ППР). Существуют и другие, связанные с анализом альтернатив, возникающих при сопоставлении нормативных, прогнозных и экспериментальных данных о надежности на разных стадиях проектирования и доводки автомобиля. В целом ППР предполагает непрерывный процесс определения характеристик надежности, реализуемый, например, следующим образом.

1. На этапе проектирования определяется априорная оценка функции распределения ресурса. Эта оценка находится путем синтеза результатов расчета на долговечность по приближенным или гипотетическим зависимостям, моделирования ресурса и ретро-спективного прогноза.

2. Уточняется априорная оценка по результатам испытаний единичных опытных образцов, например на основании теоремы гипотез (формулы Байеса).

3. Определяется апостериорная оценка функции распределения ресурса по результатам ресурсных испытаний опытной партии образцов, например в условиях автополигона, с применением методов обработки малых выборок. На основании полученных данных строится обобщенная (полная) оценка функции распределения с априорной и апостериорной компонентами.

4. На этапе испытаний подконтрольных партий серийных автомобилей в опорных автопредприятиях получаются окончательные оценки искомых характеристик классическими статистическими методами.

Согласно теории принятия решения введем понятие участвующих сторон и вариантов их стратегии с учетом специфики получения прогнозной информации при проектировании. Под одной из сторон будем понимать конструктора А, а под стратегией этой стороны - различные варианты проектируемой детали A_i. Под стратегиями второй участвующей стороны П ("природы") - варианты прогноза показателей надежности деталей.

Методы принятия решений зависят от того, имеется или отсут-ствует возможность проведения экспериментов с целью уточнения вероятности состояний стороны П. Если отсутствует возможность проведения экспериментальных исследований, а вероятности состояния "природа" - прогнозных вариантов показателей надежности - полностью не определены, то минимальное количество вариантов j ограничено двумя. Максимальное количество определяется вариантами прогноза с помощью моделей отказа, КУД и т. д. Таким образом, общее количество вариантов прогноза определяется размером матрицы А_i×Π_j, элементы которой Π_j представляют собой показатели надежности. В общем случае среди Π_j можно выделить максимальное Птах и минимальное Πⁿ_max значения, сопоставление которых с нормативным значением Π_H приводит к различным ситуациям.

Первая ситуация может быть представлена соотношением Πⁿ_min > Π_H для деталей, влияющих на безопасность движения. Условие является обязательным при отсутствии диагностики или при принудительной замене детали на установленной наработке. Если в дальнейшем не предполагается увеличения Π_H, т. е. для данного объекта исчерпаны возможности увеличения показателей надежности за счет модернизации, то конструкция детали (технология изготовления, материал) должна быть проанализирована с целью уменьшения массы, снижения ее себестоимости и т. п.

Вторая ситуация характеризуется соотношением Πⁿ_max < Π_H, которое позволяет выявить детали, лимитирующие надежность, на этапе проектирования. Для повышения надежности этих деталей в первую очередь необходимо разрабатывать мероприятия, которые условно могут быть разбиты на группы. Первая группа включает мероприятия, связанные с данной деталью или сопряжением: изменение конструкции (размеров, формы), устранение концентраторов напряжений, замена материала, выбор технологии изготовления и упрочнения, подбор смазки и режимов приработки т. д. Очевидно, к этой же группе следует отнести мероприятия, связанные с выбором рациональной стратегии замен, а также определением количества запасных частей.

Мероприятия второй группы относятся к агрегату (сборочной единице), в который входит данная деталь. Они включают разработку различных вариантов конструкции агрегата, позволяющих снизить уровень нагруженности, например путем устранения резонансных явлений, выбор рациональной периодичности технических обслуживаний, ремонтов и т. п. Необходимость в разработке мероприятий второй группы возникает в тех случаях, когда мероприятия первой группы не позволяют достичь желаемых результатов из-за ограничений на стоимостные, весовые и другие параметры или когда мероприятия второй группы требуют меньших затрат.

Третья группа включает мероприятия, относящиеся к нескольким агрегатам (или автомобилю в целом), и предусматривает главным образом конструктивные изменения. Характерным примером использования всех трех групп мероприятий являются работы по повышению показателей надежности карданных шарниров. Это упрочнение поверхностей шипа крестовины и уменьшение разно- размерности игл роликовых подшипников (первая группа), подбор смазки и способа ее подвода, а также изменение конструкции уплотнений (вторая группа), и, наконец, изменение углов наклона силового агрегата и главной передачи (третья группа). Для автомобилей МАЗ эти мероприятия в комплексе позволили повысить средний ресурс шарниров в несколько раз.

Третья ситуация характеризуется соотношением Πⁿ_min < Π_H < Πⁿ_max. Если отсутствует возможность проведения экспериментов, позволяющих конкретизировать прогнозные значения показателей надежности Πⁿ_ij, то для выбора наилучшей стратегии A_i - варианта конструкции детали - можно применить методы, основанные на использовании критериев, рассчитываемых по так называемой платежной матрице. Элементы матрицы могут быть определены различными методами и, в частности, по формуле

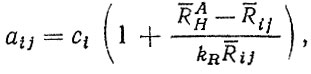
где c_i - себестоимость j-го варианта детали; R^A_H - средний нормативный ресурс агрегата (автомобиля); R_ij - средний ресурс i-го варианта детали для j-го варианта прогноза; k_R - коэффициент, учитывающий уменьшение среднего ресурса между отказами.

Величины c_i определяются расчетом или экспертным путем, В качестве R^A_H могут быть взяты средние ресурсы агрегата (автомобиля) до капитального ремонта или списания. Для выбора стратегии А_i можно применить критерий, гарантирующий величину затрат на производство и запасные части не больше максимальных k = min max a_ij.

Следовательно, при отсутствии экспериментальных данных выбор варианта конструкции детали возможен с помощью мини-максного критерия.

На этапе доводки проводятся испытания спроектированной конструкции, для которых характерным является малое количество испытываемых образцов. В этом случае уточнение прогнозных оценок показателей надежности Π_j конкретной детали может быть выполнено с использованием формулы Байеса

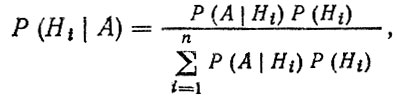(4.41)

где H_i - гипотеза о предполагаемом состоянии объекта (вариант прогноза); Р (H_i) - априорная вероятность состояния объекта; А - дополнительная информация о проведенных испытаниях, связанных с гипотезой H_i; Р (А|H_i) - условная вероятность события А; Р (H_i|А) - апостериорная вероятность состояния системы.

Пример 1. Априорные вероятности двух вариантов прогноза Р (Н₁) = Р (Н₂) = 0,5. Условные вероятности безотказной работы Р (A|H_i) определим с помощью функций распределения отказов F_i (L). Допустим, что на пробеге не было зафиксировано отказов детали. Тогда значения условных вероятностей составят

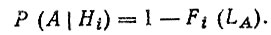
Для рассматриваемого примера примем: Р (A|H_i) = 0,4; Р (А|H₂) = 0,8. С помощью формулы (4.41) определим апостериорные вероятности вариантов прогноза

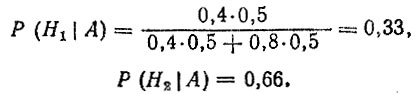
Пример 2. Положим, что R - событие, состоящее в отказе детали; Р (Н₀) - вероятность достоверности априорной оценки; Р (H₁) - вероятность ошибки в прогнозе. Тогда по формуле полной вероятности найдем вероятность отказа

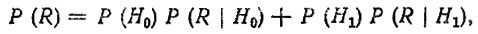(4.42)

где Р (R|Н₀) - априорная оценка вероятности отказа, определяемая по функции распределения F(L); Р (R|Н₁) - эмпирическая (альтернативная) оценка вероятности отказа по результатам испытаний. Допустим, что при испытании пяти образцов на пробеге L зафиксирован один отказ. По формуле для медианных порядковых статистик [28] найдем

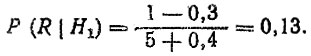
Априорная оценка Р (R|H₀) = F (L) = 0,2. Если предположить" что прогнозные расчеты достоверны на 80%, то получим Р (Н₀) = 0,8 и Р (Н₁) = I - 0,8 = 0,2. Подставив численные значения в формулу (4.42), получим полную вероятность отказа на пробеге

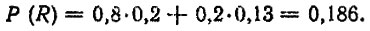
Уточненное значение функции распределения ресурса можно найти из соотношения

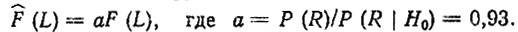
Воспользовавшись формулой Байеса, определим вероятность подтверждения прогноза после испытаний

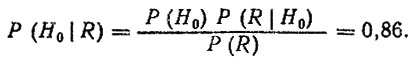
Таким образом, при наличии информации даже о небольшом числе испытанных деталей использование байесовского подхода позволяет уменьшить степень неопределенности прогнозных оценок при принятии решений.

Рассмотрим задачу управления надежностью с учетом хозяйственного риска. Найдем оптимальное количество запасных частей, хранимых на складе, исходя из условия

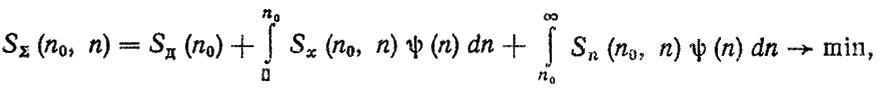
где S_д(n) - затраты на приобретение деталей; S_x (n₀, n) - издержки, связанные с приобретением избыточного количества запасных деталей; S_n (n₀, n) - убытки от неудовлетворенного спроса на детали; ψ(n) - функция плотности распределения спроса на детали; n₀ - оптимальный уровень запасов; S_Σ(n₀, n) - суммарные затраты.

Затраты на приобретение деталей определяются по формуле S_д (n) = С_д (n₀ - z), где С_д - оптовая цена детали; z - начальный запас (остаток). Стоимость хранения избыточных запасов будет равна

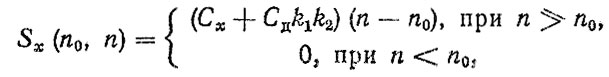
где С_х - стоимость хранения одной детали на складе; k₁ - коэффициент, учитывающий долю оборотных средств в фактических запасах, приходящихся на долю кредитов Госбанка; k₂ - коэффициент, учитывающий долю средств, уплачиваемых предприятиями банку за пользование денежными средствами, полученными в ссуду за сверхнормативный запас.

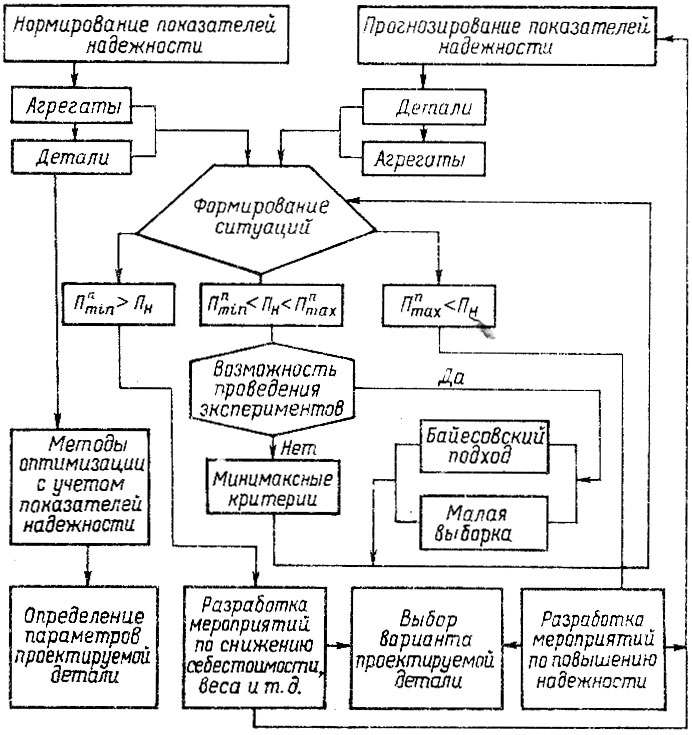
Рис. 4.5. Схема принятия решений но управлению надежностью на основе прогнозной информации

При т < т₀ имеет место неудовлетворенный спрос. Убытки от неудовлетворенного спроса можно определить по времени простоя автомобилей в ожидании новой поставки деталей

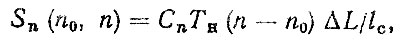
где С_т - убытки от простоя одного автомобиля в течение часа; Т_н - время в наряде; l_с - суточный пробег; ΔL - не до пробег автомобиля по причине отсутствия отказавшей детали на складе.

Величину ΔL можно найти, если известна функция распределения ресурса детали. Например, для распределения Вейбулла получим

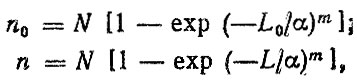
где N - списочное число автомобилей.

Разрешая уравнения относительно L₀ и L, найдем

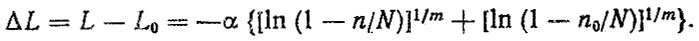
Плотность распределения - спроса ψ(n) может быть задана, получена в результате анализа статистических данных или смоделирована методом Монте-Карло, если известны распределения пробега автомобилей между поставками φ(l_n) и с начала эксплуатации φ(l_n) по формуле

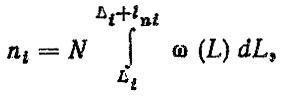
где ω(L) - параметр потока отказов; L_i - случайная наработка автомобиля на момент завоза деталей на склад; lni - случайная наработка автомобиля между поставками деталей.

Подставив выражения для различных статей затрат и ψ(n) в исходное уравнение" получим типичную задачу оптимизации, которую можно решить, например, методом случайного поиска. Изложенное можно обобщить в виде блок-схемы принятия решений по управлению надежностью на основе прогнозной информации, представленной на рис. 4.5. Отметим, что применение рассмотренных методов открывает путь к существенному сокращению объемов и продолжительности различных испытаний, дает возможность получать достаточно объективную информацию о надежности деталей на ранних стадиях испытаний и эксплуатации автомобилей, что крайне необходимо для управления их надежностью.