4.2. Методы оптимизации конструкций с учетом надежности

Когда все управляемые x_i и неуправляемые α_j параметры, влияющие на некоторый критерий или показатель эффективности W (q_k) конструкции, определены, задача оптимизации сводится к нахождению таких x_i, которые обеспечивают минимум (максимум) целевой функции

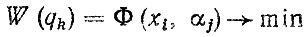(4.35)

при ограничениях на параметры типа. А_i ≤ x_i ≤ В_i, c_j ≤ α_j ≤ D_j и L_i (x_i, α_j) = 0. В общем случае критерий W (q_k) определяется совокупностью частных критериев qh. Такую постановку задачи оптимизации принято называть детерминированной.

Рассмотрим пример определения оптимальных размеров трубы карданного вала автомобиля, приняв в качестве критерия оптимизации ее вес. При определении конструктивных параметров карданной передачи выполняют расчет элементов на прочность, устойчивость и долговечность Полагая сечение трубы вала кольцевым, постоянным по всей длине, получим целевую функцию

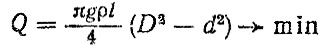
и систему ограничений по прочности

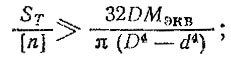
критической частоте вращения (устойчивости)

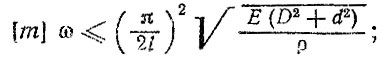
технологическим требованиям

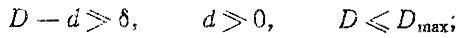
долговечности [41 j (например, для релеевского распределения)

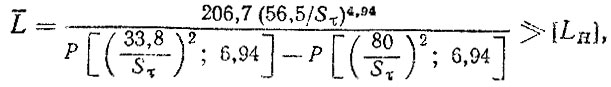(4.36)

где D, d - наружный и внутренний диаметры; ρ, Е - плотность материала и модуль упругости соответственно; I - длина трубы карданного вала; M_экв - эквивалентный момент; S_T - предел текучести; [n], [m] - коэффициенты запаса по прочности и устойчивости соответственно; Р [ ] - табулированные функции Р (χ², n)[41]; S_τ - амплитуда напряжений, определяемая через амплитуду момента S_M по формуле

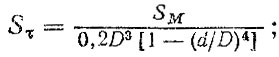
[L_H] - назначенный ресурс трубы карданного вала.

Положим: ω = 334 с^-1; M_акв = 3370 Н⋅м; δ = 0,6 см; l = 171 см; D_max = 15,0 см; [m] = 1,2; [n] = 1,5; S_M = 618 Н⋅м, [L_H] = 150 тыс. км. Приведем ограничения по устойчивости и прочности к нормальному виду

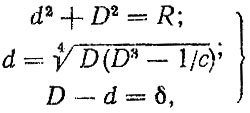(4.37)

Подставив численные значения параметров в формулы (4.37), найдем область допустимых значений (ОДЗ) в виде уравнений:

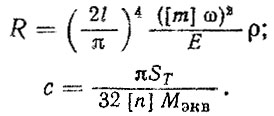
Графическое изображение целевой функции и ее горизонтальной проекции с ОДЗ представлено на рис. 4.4, из которого видно, что оптимум достигается на границе области в точке пересечения двух линий. Решая совместно систему уравнений

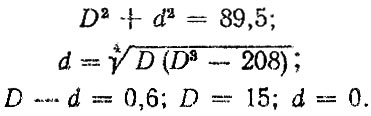
получим 2,4d³ + 2,16d² - 207,2d = 324,7 откуда D₀ = 9,75 см и d₀ = 9,15 см. Найденные значения диаметров обеспечивают минимально возможный вес Q = 11,83 кг и удовлетворяют всем заданным ограничениям, включая ограничение по долговечности

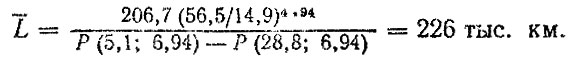
Если кроме управляемых и неуправляемых параметров в задаче (4,35) оговорены некоторые случайные факторы Y_j, то речь идет о нахождении решения в условиях неопределенности. Наиболее характерными задачами оптимизации, возникающими при проектировании автомобилей, являются следующие:

1. Определение наиболее вероятной прогнозируемой оценки ресурса деталей при заданных условиях эксплуатации, материалах и технологиях изготовления и упрочнения.

2. Оптимизация ресурса изделия с экономической точки зрения при заданных условиях эксплуатации и затратах на восстановление. В этом случае минимизируются затраты на изготовление изделия варьированием материалами, технологией, размерами.

3. Выбор материала изделия, размеров и технологии изготовления при заданных условиях эксплуатации и ресурсе при условии минимизаций затрат на изготовление и восстановление.

4. Оптимизация условий эксплуатации (режимов) при заданных ресурсе изделия, материалах, технологии и размерах.

5. Максимизация ресурса при заданных условиях эксплуатации и затратах на изготовление и восстановление изделия.

Перечень задач оптимизации можно продолжить, если ввести другие критерии или несколько критериев, например технические, экономические и т, д. Однако в каждом случае корректная постановка задачи требует наличия соответствующей системы ограничений, В каждом из случаев 2, 3, 4, 5 на этапе проектирования решается локальная задача оптимизации, т. е, прогнозируется наиболее вероятная оценка ресурса.

Нормативные показатели надежности обычно используются в уравнениях связи, входящих в ограничения типа (4.35). Допустим, что модель отказа детали формируется с учетом N независимых разрушительных процессов. При наличии плотности распределения нормативного ресурса f_н (R) ограничение согласно (4.35) будет иметь вид

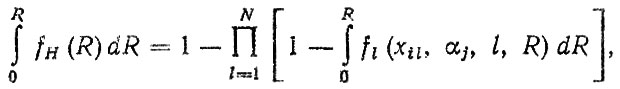(4.38)

где f_l (x_il, α_j, f, R)-плотность распределения для i-го вида разрушительного процесса.

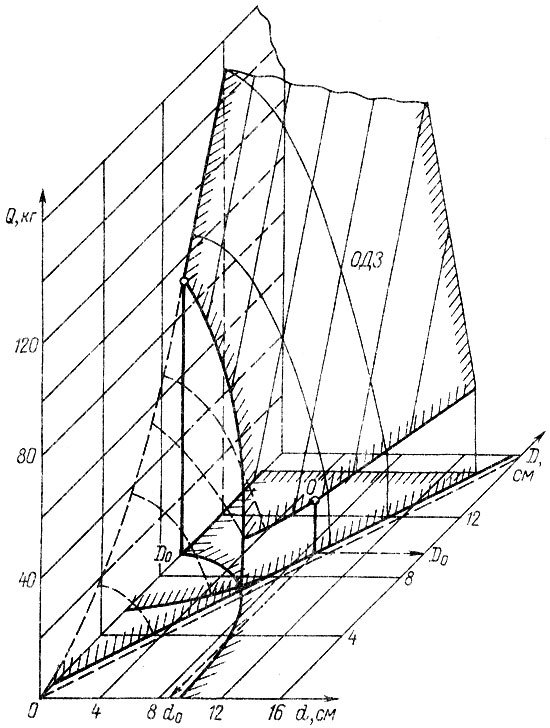
Рис. 4.4. Целевая функция, ограниченная областью допустимых значений (ОДЗ) параметров

Вместо интегрального представления (4.38) можно воспользоваться уравнениями связи, содержащими моменты распределений f_н (R) и f_i (R), или потребность равенства функций распределения при определенных, установленных значениях R. Очевидно, число таких уравнений ограничивается количеством параметров распределения f_H (R).

При наличии не определенностей решение оказывается приближенным. Например, если f_i (R) получено при расчетах на усталость по гипотезе суммирования повреждений, то неясность в выборе варианта гипотезы приводит к неопределенности "оптимальных" размеров проектируемой детали. Можно сказать, что при двух вариантах требуемый размер dn подчиняется неравенству d_I < d_n < d_II. Следовательно, ввиду природной неопределенности найденные решения (d_I, d_II) позволяют ограничить область возможных значений d_n. Окончательное решение относительно d_n принимается после испытаний.

При расчетах на статическую прочность в некоторых случаях удается получить аналитические выражения для ограничений, когда нормативный показатель надежности задан в виде вероятности безотказной работы Р_H. Если для каждого из N сечений детали производится расчет с использованием модели 2.2 (см. табл. 2.4), то уравнение связи (4.38) записывается в виде

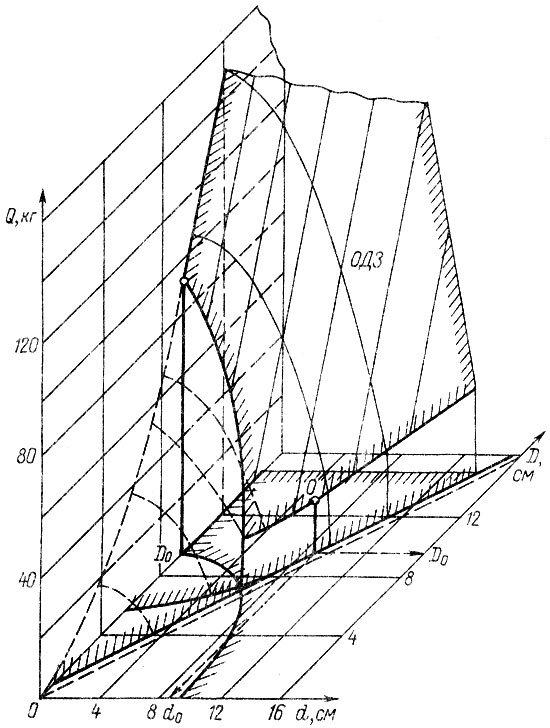(4.39)

Поскольку для большинства деталей можно не учитывать изменение статических характеристик пределов прочности (текучести), связанных, например, с абсолютными размерами, то в формуле (4.39) l_R (R) принимается постоянной для всех сечений.

В случае, когда плотности распределения нагрузки l_R (S) и прочности f_sl (R) подчиняются нормальным законам распределения, получим

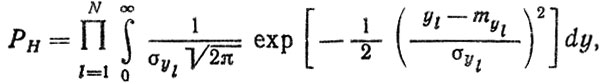(4.40)

где

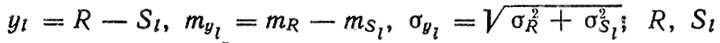
соответственно случайные величины прочности и нагрузки в l-м сечении детали.

При N = 1 из (4.40) следует зависимость, приведенная в работе [28].