Глава 4. Управление надежностью при проектировании на основе прогнозной информации

4.1. Нормирование показателей надежности проектируемых агрегатов и деталей

Надежность и эффективность. Управление надежностью автомобилей на всех стадиях их создания и эксплуатации является самостоятельной, в настоящее время недостаточно изученной проблемой. Как один из показателей потребительских свойств надежность тесно связана с эффективностью и поэтому управление надежностью автомобилей есть в большой степени и управление их эффективностью.

Под эффективностью технической системы в общем случае понимается ее способность выполнять требуемые функции при заданных условиях производства и эксплуатации. Следовательно, согласно ГОСТ 27.002-83 надежность можно рассматривать как свойство сохранять эту способность во времени.

Количественная оценка эффективности, как и надежности, неоднозначна. В качестве ее измерителей используют технические, экономические, информационные, вероятностные, а также комплексные и обобщенные критерии [11, 59]. Нередко эффективность просто отождествляют с такими экономическими понятиями, как прибыль или ее прирост, срок окупаемости, коэффициент эффективности капитальных вложений, приведенные затраты и т. п. Это вполне объяснимо с практических позиций, поскольку вычисление обобщенных [11] или вероятностных критериев [59] с учетом экономических факторов сопряжено не только со сложными вычислительными процессами, но и с подготовкой и обработкой большого количества вспомогательной информации. В свою очередь, получение подобной информации требует проведения дополнительных экспериментальных исследований, что не всегда возможно. Большинство комплексных критериев эффективности, несмотря на относительную простоту, достаточно полно учитывают надежность. В частности, для оценки эффективности автомобилей часто применяют приведенные затраты на их изготовление и эксплуатацию

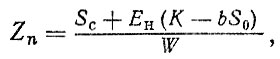(4.1)

где W среднегодовая производительность; S₀ - стоимость; К - капитальные вложения на создание и эксплуатацию автомобиля; Е_H - нормативный коэффициент эффективности капитальных вложений; b - коэффициент, учитывающий остаточную стоимость; S_c - суммарные эксплуатационные затраты.

Здесь фактическая производительность W прямо связана с комплексным показателем надежности - коэффициентом готовности. Затраты S_c определяются через потоки отказов и восстановлений автомобиля, а капитальные вложения К, включающие его первоначальную стоимость, отражают надежность косвенно через используемые материалы, технологию и организацию производства и эксплуатации. Все три параметра К, S_c и W коррелируются с надежностью (и с ее повышением); за счет увеличения капитальных вложений растет величина W и снижается значение S_c, Очевидно, конструкция, имеющая меньшую по сравнению с аналогом величину Z_n, может считаться более эффективной экономически. Надежность автомобиля определяется совокупностью свойств - безотказностью, долговечностью, ремонтопригодностью и сохраняемостью, неразрывно связанных между собой. Эту связь можно изобразить схематично (рис. 4.1), вложив в понятие сохраняемости по ГОСТ 27.002-83 более широкий смысл и распространив его на период нормальной эксплуатации. Поток отказов со (L) автомобиля, агрегата или отдельной детали определяется их безотказностью Б. Для не восстанавливаемых деталей понятия безотказности и долговечности Д совпадают. Поток отказов восстанавливаемых изделий формирует соответствующий поток затрат S_Б(L)f который может служить критерием оптимизации долговечности деталей или агрегатов и нормирования потока замен δ (L). Требуемая ремонтопригодность Р определяется агрегированием потоков со (L) и б (L) и соответствующих им потоков затрат S_Б (L) и S_Д (L) в поток восстановлений λ (L). Сохраняемость, рассматриваемая здесь как свойство объекта сохранять заданную надежность в процессе эксплуатации, оценивается потоком списаний h (L) и соответствующим ему потоком суммарных эксплуатационных затрат S_c (I). Потоки затрат определяются уравнениями

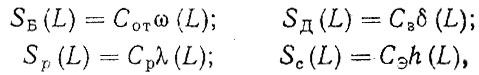
где С_от, С_з, С_р, С_Э - стоимость устранения отказа, замены, ремонта и эксплуатации объекта соответственно.

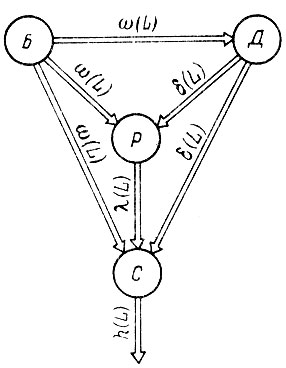
Рис. 4.1. Схема формирования свойств, определяющих надежность автомобиля: ω (L) - поток отказов; δ(L) - поток замен; λ (L) - поток восстановлений; h (L) - поток списаний

Таким образом на основании схемы (см. рис. 4.1) с использованием критерия (4.1) можно решать задачи нормирования надежности не только автомобиля в целом, но и отдельных его агрегатов, сборочных единиц и других составных частей.

К достоинствам критериев типа (4.1) относится наличие имеющей экстремум (минимум) функциональной зависимости Zn от надежности технической системы. Это позволяет решать задачи нормирования целого ряда характеристик надежности исходя из принципа максимизации экономической эффективности (т. е. минимума Z_n). Известен ряд исследований [76, 79], в которых на основе рассмотренного принципа разработаны алгоритмы определения экономически оптимальных ресурсов и сроков службы сложных технических систем. Однако в целом эти алгоритмы ориентированы на использование экспериментальной информации, получаемой из опытной эксплуатации серийных машин, что ограничивает их возможности в части нормирования характеристик надежности новых объектов на стадии проектирования.

В реальных условиях трудно ожидать строго детерминированных связей между свойствами конструкции или отражающими их характеристиками, Поэтому правильнее представлять критерии эффективности" в том числе и комплексные, случайными величинами. Тогда количественно эффективность системы будет'выражаться вероятностью выполнения возложенных на нее функций в заданной совокупности ограничений на критерий или критерии эффективности. В этом случае задача нормирования надежности (либо какого-нибудь другого свойства) будет решаться исходя из принципа максимизации эффективности (т. е. вероятности). Например, если Z_n - случайная величина с плотностью распределения f (Z_n), то следует искать решение, удовлетворяющее условию

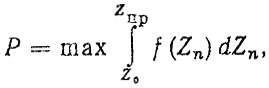(4.2)

где (Z₀,..., Z_ΠP) - область допустимых значений критерия эффективности Z_n.

Еще одна важная особенность реальных ситуаций заключается в том, что не все важные свойства автомобиля могут быть отражены в комплексном критерии через денежный или приведенный денежный эквивалент. Иногда самостоятельными, не менее существенными, чем экономичность, могут оказаться такие свойства, как безотказность, безопасность, экологичность, комфортность и т. п. Для оценки эффективности в этом случае наиболее приемлемым будет обобщенный вероятностный критерий

где А - область допустимых значений совокупности критериев (показателей) x₁, x₂,...,x_n отражающих все учитываемые свойства объекта; f (x₁, x₂,...,x_n) - совместная плотность распределения.

Задача нормирования надежности в этом случае принципиально не отличается от одномерного варианта (4,2).

Схематизация объектов проектирования. Надежность сложных технических систем определяется надежностью составляющих их элементов. Разработанные в теории надежности математические методы позволяют решать широкий круг задач нормирования показателей безотказности, долговечности и ремонтопригодности при условии, что надежность составляющих систему элементов известна. Это так называемые прямые задачи. При проектировании новых сложных объектов возникают обратные задачи, связанные с распределением требований к надежности элементов, исходя из заданных в техническом задании характеристик надежности всей системы. Обратные задачи существенно сложнее прямых и требуют для решения допущений и ограничений на функциональные и структурные внутрисистемные связи, а также определенной идеализации условий эксплуатации. Проектируемую конструкцию удобно анализировать в схематизированном виде, например, как граф переходов, отражающий функциональные связи, или как структурную схему, определяющую конфигурацию объекта.

Автомобиль можно представить четырехуровневой иерархической структурой типа "дерево": автомобиль - агрегаты - сборочные единицы - детали (рис. 4.2). На каждом уровне образуются свои подсистемы декомпозиции. Такая схематизация позволяет исследовать подсистемы отдельно, используя для нормирования надежности их составляющих частей простейшие двухуровневые структуры типа "система-элементы". Таким образом, начиная с первого уровня, рекуррентно вычисляются характеристики надежности всех элементов схемы от агрегатов до простейших деталей. На каждом новом шаге нормирования системой будет являться один из элементов более высокого иерархического уровня, надежность которого определена на предыдущем шаге. Например, на втором шаге агрегат А₂ (см. рис. 4.2) будет "системой" по отношению к элементам У₁ У₁,....,У_m.

Большинство подсистем автомобиля обладает простой конфигурацией с характерным последовательным или последовательно параллельным соединением элементов [60]. При необходимости упрощения схем соединения до простейших можно в общую структуру вводить дополнительные иерархические подуровни.

Нормирование безотказности. Безотказность системы, состоящей из n статистически независимых последовательно соединенных элементов на некоторой наработке L, определяется зависимостью

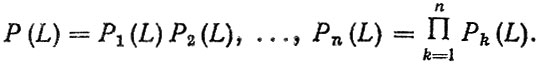(4.3)

При равномерном распределении требований к безотказности элементов из (4.3) получим

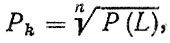(4.4)

где Р (L) - задаваемая в техническом задании установленная безотказность системы.

Возможности нормирования безотказности механических систем по формуле (4.4) весьма ограничены из-за сложности обеспечения равнопрочности элементов. Обратимся к основной формуле вероятности безотказной работы

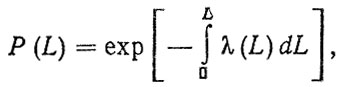(4.5)

где λ(L) - интенсивность отказов.

С учетом (4.3) для системы из n элементов получим

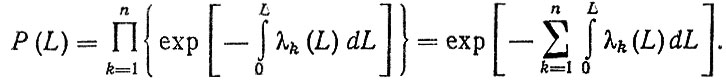(4.6)

При заданной безотказности системы на некоторой установленной наработке L = L_y, полагая γ = Р (L_y), имеем

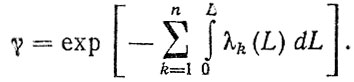(4.7)

Из (4.7) видно, что существует множество λ_k (L), обеспечивающих требуемую безотказность системы γ, Поэтому для решения задачи нормирования надежности элементов необходима дополни" тельная информация об интенсивностях λ_k (L). Воспользуемся традиционным представлением λ_k (L) как функции от пробега по аналогии с износом деталей. На этапе нормальной эксплуатации интенсивность отказов λ_k (L) ≈ const. Если пренебречь периодом при работки и считать недопустимыми износовые отказы" из (4.7) можно получить

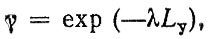(4.8)

где λ - интенсивность отказов системы

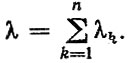
Полученное соотношение справедливо для экспоненциальных законов распределения наработок элементов до отказа с параметрами λ_k, для которых, вероятности безотказной работы определяются по формуле

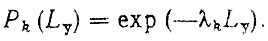(4.9)

Безотказность восстанавливаемых изделий определяется с учетом потоков их отказов и восстановлений. Восстановление работе" способности системы, осуществляемое ремонтом, регулировкой или заменой одного из элементов, может происходить в нерабочее время без снятия системы с эксплуатации. Это соответствует модели "мгновенного" восстановления и предопределяет равенство потоков отказов и восстановлений, что существенно упрощает задачу нормирования безотказности системы.

В общем случае потоки отказов механических систем являются нестационарными, сложным образом меняющимися во времени, Это делает задачу нормирования надежности трудно разрешимой аналитически. Очевидно, наиболее эффективным путем ее решения с учетом нестационарности и других особенностей потоков является статистическое моделирование наработок элементов L_jh и системы L_oj ЭВМ по заданным распределениям f_k (L) с использованием, напр мер, принципа слабейшего звена

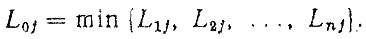(4.10)

В частном случае, когда f_i (L) подчиняются экспоненциальному закону, формируется поток с λ_k = const (простейший поток). Вероятность безотказной работы системы с резервированием при простейшем потоке отказов определяется формулой Пуассона

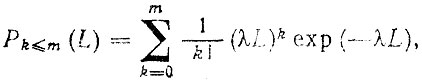(4.11)

где m - допустимое число отказов (замен) элементов, не приводящее к отказу системы; λL = h.

Фактически Р_k≤m (L) означает вероятность того, что за наработку L число отказов k будет не больше m. Если понятие отказа для системы определено и заданы m и P_k≤m (L)% то величину λ можно найти по таблицам табулированных функций [63] или численно.

Полагая потоки отказов элементов также простейшими, получим

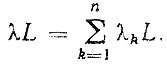(4.12)

Упрощение задачи путем сведения потоков отказов к простейшим на стадии проектирования машин практически обосновано.

Неточности в вычислениях в этом случае возможны только в сторону запаса надежности.

Из формулы (4.12) видно, что существует неопределенное множество λ_k, обеспечивающее установленный поток отказов h = λL системы. Для устранения этой неопределенности можно воспользоваться методом весовых коэффициентов [28], не противоречащим принятым допущениям. Полагая весовые коэффициенты W_k известными или заданными априори, можно найти оценки безотказности элементов на наработке L:

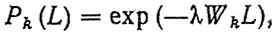(4.13)

поскольку

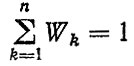
и из (4.14) следует

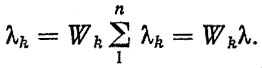
Соответственно вероятность отказа j-го элемента на наработке L будет

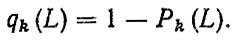
Таким образом, метод весовых коэффициентов, задаваемых априори, позволяет решить задачу нормирования безотказности элементов системы на установленной наработке L при условии, что поток отказов является простейшим с суммарной интенсивностью

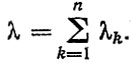
При этом полагается, что все составляющие λ_k = λW_k малы по сравнению с λ, т. е. в системе нет элементов, потоки отказов которых были бы сравнимы по интенсивности с потоком отказов всей системы.

Определение весовых коэффициентов W_k, учитывающих важность, или относительную значимость, элементов в системе, представляет собой самостоятельную задачу. Оценки W_k можно найти по формуле

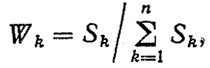
де S_k - априорный оценочный показатель для k-го элемента, найденный в результате испытаний или назначенный по принципу аналогии с подобными уже известными системами,

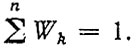
В качестве показателей S_k могут быть приняты удельные затраты на эксплуатацию системы, трудоемкости устранения отказов, долговечности, безотказность или интенсивность отказов аналогов λ_k' и т. п. В частности при S_k = _k' имеем

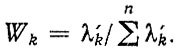
Рассмотрим пример распределения требований к безотказности элементов методом весовых коэффициентов, воспользовавшись результатами моделирования на ЭВМ потоков отказов 40 автомобильных двигателей на пробеге до 170 тыс. км [39]. По характеру потоков можно предположить, что к данной наработке они стабилизировались, В табл. 4.1 приведены осредненные весовые коэффициенты для стабилизированных потоков, найденные различными

способами (а также вероятности безотказной работы элементов):

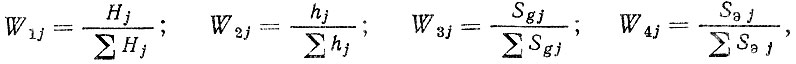
где H_j - ведущие функции потоков отказов, определяемые общим количеством замен; S_gj - затраты на запасные части; S_Эj- общие эксплуатационные затраты; h_j = λ_jΔL - потоки отказов.

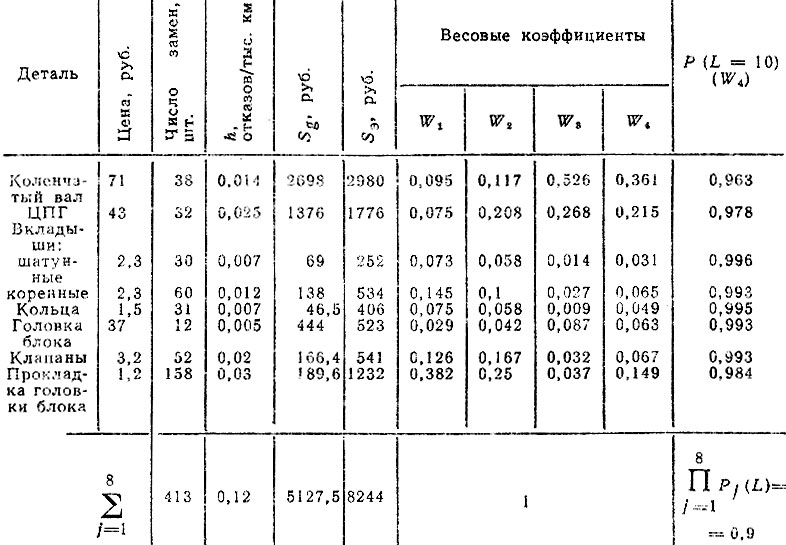
Таблица 4.1. Определение весовых коэффициентов для нормирования безотказности двигателя

Из приведенных данных видно, что выбор критерия существенно влияет на оценку важности того или иного элемента. Коэффициенты по-разному и в различной степени учитывают их надежность: W₁ - только долговечность; W₂ - безотказность и долго-вечность; W₃ - долговечность деталей с учетом их стоимости; W₄ - комплексно учитывает безотказность, долговечность и ремонтопригодность через затраты на восстановление работоспособности двигателя. Вычислим требуемую безотказность элементов вновь проектируемого двигателя на установленной наработке ΔL_y = 10 тыс. км, воспользовавшись коэффициентами W4. Для системы без ЗИПа из (4.11) имеем h = λL_y = -In у, где у - требуемая безотказность двигателя на наработке ΕL_y. Приняв γ = 0,9, получим h = 0,105 или λ = 0,0105. По формуле (4.15) для коленчатого вала найдем Р₁ (L = 10) = ехр (-0,105⋅0,361) = 0,962.

Для дальнейшего нормирования безотказности деталей двигателя можно ввести дополнительные иерархические подуровни. Например, ДПГ можно представить как систему, состоящую из восьми одинаковых последовательно соединенных элементов. Тогда [согласно (4.4)1 безотказность каждого из них будет

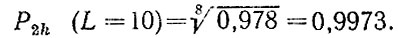
При комплектации отдельных элементов ЗИПом на этом же подуровне может быть образована система из одинаковых параллельно соединенных элементов. Так, при наличии двух запасных прокладок для двигателя получим

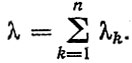
Рассмотренный метод нормирования соответствует потокам с λ_k = const, которые могут иметь место при экспоненциальном распределении наработок до отказа или на этапе нормальной эксплуатации системы со средней наработкой на отказ ΔL_y при заданной вероятности γ.

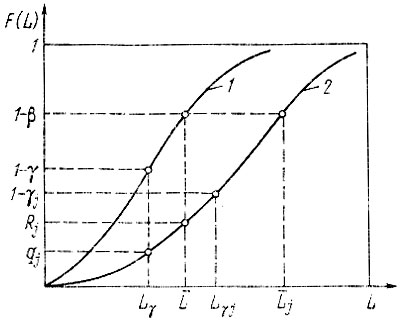
Рис. 4.3. Функции распределения наработок до отказа: 1 - системы; 2 - j-го элемента

Рассмотрим приближенный метод оценки средней и гамма-процентной наработок до отказа элементов, воспользовавшись рис. 4.3. Положим, что L и L_j - средние наработки до отказа системы и j-го элемента; L и L_j - установленные наработки до отказа системы и j-го элемента при уровнях безотказности L_γ и Lγj соответственно; β - вероятность безотказной работы, соответствующая средней наработке до отказа; q_j и R_j - вероятности возникновения отказа j-го элемента на установленной L_γ и средней L наработках системы. Согласно условию безотказности (4.3) для n элементов

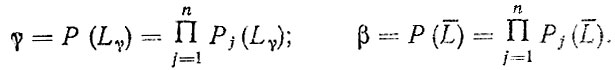(4.15)

Вероятности q_j и R_j вычисляются по формулам:

(4.16)

где

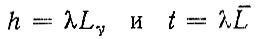
находятся из уравнения (4.11) при

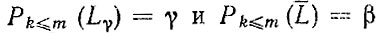
соответственно.

Допустим, что существуют линейные преобразования

(4.17)

Для нормального закона распределения наработок до отказа, используя его свойства и рис. 4.3, можно записать

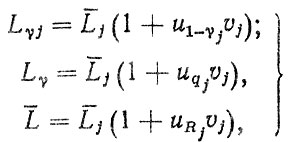
где U($) - квантили нормированных нормальных распределений, соответствующие вероятностям 1 - γ_j, q_j и R_j, υ_j - коэффициент вариации наработки до отказа j-го элемента.

Из первого и второго уравнений после деления одного на другое и преобразований полученного выражения совместно с третьим уравнением с учетом (4.17) находим:

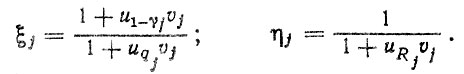
Коэффициенты вариации υ_j можно найти в результате совместного решения второго и третьего уравнений

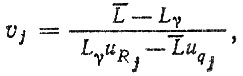
учитывая, что

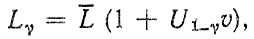
где υ - коэффициент вариации наработок до отказа системы.

Для распределения Вейбулла, поступая аналогичным образом, имеем:

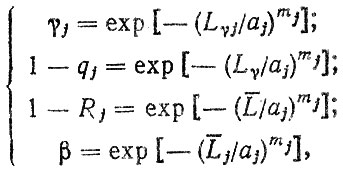
где a_j, m_j - параметры распределения Вейбулла.

После логарифмирования и совместного решения первых двух уравнений найдем

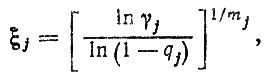
где m_j можно вычислить по формуле

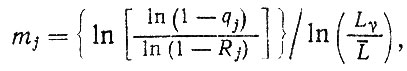
получаемой в результате совместного решения второго и третьего уравнений.

Решая совместно третье и четвертое уравнения, получим

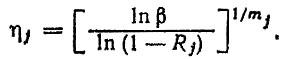
Обратимся к рассмотренному ранее примеру, Полагая распределение наработок до отказа двигателя и его элементов экспоненциальными (распределение Вейбулла с р = 0,368 и m = 1), получим L_j = 1/λ_j = 1/λW_j. Для коленчатого вала, например, L₁ = 1/(0,0105⋅0,361) = 264 тыс. км и

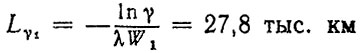
при γ = 0,9.

Нормирование долговечности. Рассмотрим нормирование долговечности агрегатов и деталей исходя из условия, что для проектируемой машины заданы некоторые показатели, например установлен гамма-процентный ресурс до первого капитального ремонта. Разобьем общую задачу на два этапа; первый - определение нормируемых показателей для агрегатов; второй - определение нормируемых показателей для деталей каждого агрегата.

Рассмотрим возможные формулировки задач первого этапа.

Задача 1. Для машины, включающей n агрегатов, при наработке k_γ, соответствующей гамма-процентному ресурсу, допускается k первых замен агрегатов, k < n. Требуется определить параметры ресурсов агрегатов, например среднее значение R_a и среднее квадратическое отклонение σ_а.

Допустим, что случайные величины ресурсов агрегатов независимы и подчиняются одному закону с функцией распределения F (x). Тогда начальные условия можно представить следующим образом;

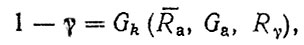(4.18)

где G_k - функция распределения наработки k-го агрегата при наработке R_γ.

Если над случайной величиной x с функцией распределения F(x) производить n независимых опытов и наблюдаемые значения располагать в порядке возрастания Z₁, Z₂,.., Z_n, то функция распределения k-го из них записывается в виде [10]

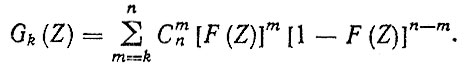(4.19)

При значениях m < n/2 формулу (4.18) удобно записать так

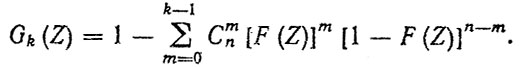(4.20)

Нетрудно показать, что при k = 1, что соответствует замене только одного агрегата на пробеге с начала эксплуатации до R_γ, приходим к функции распределения минимальных значений

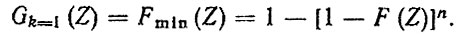(4.21)

Для конкретизаций общих формул (4.18) - (4.21) примем, что F (х) имеет распределение Вейбулла

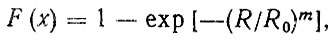(4.22)

где m, R₀ - параметры распределения.

На основании априорной информации об аналогичных агрегатах зададимся значением коэффициента вариации υ. Воспользовавшись известной аналитической зависимостью или таблицей [41], находим m = f₁ (υ) и искомое среднее значение R_a = R₀d, где d - коэффициент, d = f₂ (υ).

Если допустима замена одного агрегата, то при подстановке выражения для F (x) в формулу (4,21) получим

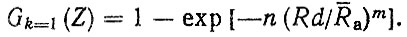(4.23)

Затем, по формуле (4.18) после преобразований находим нормативный средний ресурс агрегата

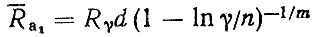(4.24)

и среднее квадратическое отклонение

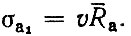
Например, при R_γ = 300 тыс. км, γ = 0,9, n = 5 и υ = 0,3 имеем m = 3,75, d = 0,9, R_a1 = 755 тыс. км, σ_a1 = 226 тыс. км.

Для тех же начальных условий, но при допустимой замене двух агрегатов формула (4.18) после упрощения запишется в виде

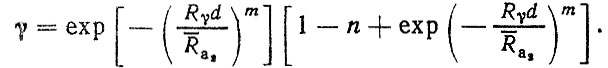(4.25)

Уравнение (4.25) относительно решается численно или графически. Из качественного анализа уравнения (4.25) следует,что R_a2 < R_a1.

Задача 2. В автомобильной промышленности при нормировании ресурсов агрегатов до первого капитального ремонта имеют место два случая: гамма-процентные ресурсы всех агрегатов равны гамма-процентному ресурсу автомобиля, т, е. R_γ = L_γ; для группы k агрегатов устанавливаются значения R_γk, а для остальных n - k агрегатов R_γ = L_γ, причем R_γk < L_γ. Требуется определить нормативные показатели ресурса и число замен агрегатов.

Рассмотрим первый случай. На основе априорной информации зададимся коэффициентами вариации ресурсов агрегатов υ_a и видами законов распределения. Тогда, нормативные параметры ресурса агрегата, в частности R_а, σ_а, можно определить из решения уравнения

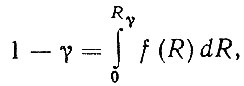(4.26)

где f (R) - плотность распределения ресурса агрегата.

Так как для нормального закона распределения

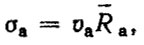
то после упрощения

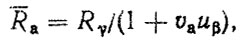(4.27)

где u_β - квантиль нормального закона, соответствующая вероятности β = 1 - γ, Очевидно, для усеченного нормального закона формула (4.27) может быть уточнена.

Аналогично" для двух параметрического распределения Вейбулла

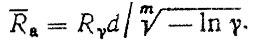(4.28)

Например, при R_γ = 300 тыс., км, γ = 0,9, υ_a = 0,3 для нормального закона имеем u_β = -1,282, R_a = 488 тыс. км, σ_a = 145 тыс. км. Для распределения Вейбулла R_a = 492 тыс. км. Отметим, что средние ресурсы практически совпали"

Воспользовавшись биноминальным законом распределения, определим математическое ожидание и дисперсию замен агрегатов по формулам:

где n - число агрегатов. Так, при n = 5, γ = 0,9 имеем m_x = 0,50, D_x = 0,45 (а_х - 0,67), т. е. в среднем у двух автомобилей потребуется замена одного агрегата.

Рассмотрим второй случай. При тех же допущениях относительно υ_a и законов распределения определение нормативных параметров ресурсов агрегатов первой группы (R_ak, σ_ak) производится по формуле (4.26) при подстановке R_γk. Выведем формулы для математического ожидания и дисперсии числа замен агрегатов.

1. На основании R_ak, σ_ak и вида закона распределения находим вероятность безотказной работы P₁ на пробеге R_γ по формуле (4.18) для первой группы агрегатов" Очевидно, Р₁ < Р₂ = γ, где Р₂ - вероятность безотказной работы второй группы агрегатов.

2. Вероятности числа замен агрегатов Р_m,n, где m = 0, 1,...,n, определяются на основании общей теоремы о повторении опытов [8] из уравнения

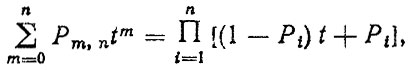(4.29)

где t - произвольный параметр; Р_i - вероятность не появления события в i-ом опыте (вероятность безотказной работы).

Для нашего случая формула (4.29) записывается в виде

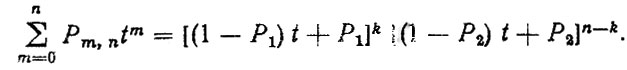(4.30)

Искомые значения Р_m,n равны коэффициентам при соответствующих степенях t правой части уравнения (4.30) после приведения подобных членов.

3. Математическое ожидание и дисперсия числа первых замен рассчитываются по формулам

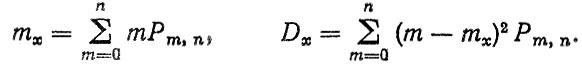
Таким образом, приведенные формулы позволяют в первом приближении оценить нормативные параметры ресурсов агрегатов исходя из заданных значений для объекта в целом.

На втором этапе на основании нормативных показателей надежности агрегата R_а, σ_а и закона распределения F_a (R), полученных на первом этапе, требуется определить нормативные показатели надежности для основных деталей агрегата. Если воспользоваться технико-экономическим методом оценки ресурса, то речь пойдет о решении обратной задачи, когда по известной функции распределения F_a (R) требуется найти функции распределения ресурса агрегата по техническому F_T (R) и экономическому F_Э (R) критериям, т. е.

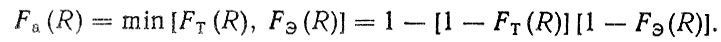(4.31)

Оптимальное решение может быть найдено с учетом дополни" тельных условий (уравнений связи, ограничений).

Рассмотрим частный случай, когда F_a (R), F_T (R) и F_Э (R) подчиняются распределению Вейбулла (4,22) с коэффициентами вариации υ_a = υ_T = υ_Э = υ. Тогда после упрощения (4.31) получим

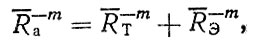(4.32)

где R - средние значения ресурсов.

Допустим, что для базовой детали, определяющей ресурс агрегата по техническому критерию, можно записать

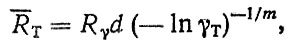
где γ_T соответствует наработке R_γ базовой детали,

Если R_a определено по формуле (4.28), то при подстановке выражений для R_a и R_T в формулу (4.32) находим

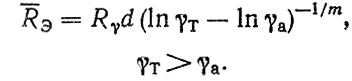(4.33)

Например, при γ_a = 0,9, γ_T = 0,98, R_γ = 300 тыс. км, m = 3,75 и d = 0,9 получим R_а = 488 тыс. км, R_T = 764 тыс. км и R_Э = 520 тыс. км.

Для оценки среднего ресурса деталей агрегата до первого отказа L₁ обратимся к формуле (3.68)

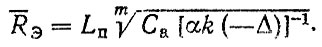
Попытаемся выразить из нее L_q. Для этого ограничимся корреляционными зависимостями σ_q = aL_q, L₁₂ = bL_q, σ₁₂ = cL₁. Тогда соответствующие выражения для L_Π, Δ и m запишутся в виде;

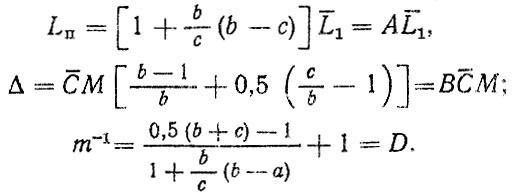
После подстановки полученных выражений в формулу для R_Э находим

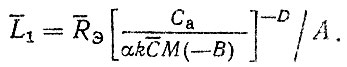(4.34)

Величины С_а, α, k, С, М и другие определяются на основе информации об аналогичных деталях и агрегатах и методов прогнозирования.

Например" при С_а = 200 руб, С = 5 руб, М = 8, α = 1,5, & = 2, а = 0,4, b = 0,5, с = 0,3 получим нормативные показатели "средней" детали агрегата: средний ресурс L₁ = 367 тыс. км; среднее квадратическое отклонение σ₁ = 147 тыс. км; гамма-процентный ресурс (γ = 0,9) по формуле (4.27) = 178 тыс. км.

Необходимо отметить, что формула (4.34) позволяет оценить среднее значение средних ресурсов деталей, лимитирующих надежность, или критических по надежности. Очевидно, для остальных деталей агрегата нормативные показатели среднего и гамма процентного ресурсов должны быть больше L₁ и R_γ.

Несмотря на то, что полученные оценки нормативных показателей надежности агрегатов и деталей являются приближенными, они могут быть использованы в процессе принятия решений при сопоставлении с прогнозными оценками на этапе проектирования.