3.5. Расчет комплексных показателей надежности агрегатов и автомобиля

Согласно ГОСТ 27,002-83, комплексный показатель надежности количественно характеризует не менее двух ее основных составляющих, например, безотказность и ремонтопригодность. Так, комплексный показатель надежности - коэффициент готовности K_Γ - определяется по формуле

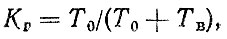
где Т₀ - наработка на отказ (безотказность); Т_в - среднее время восстановления (ремонтопригодность).

На автомобильном транспорте применяют ряд технико-эксплуатационных показателей [37, 65], среди которых наиболее важными являются коэффициент технической готовности К_{т. г} и коэффициент выпуска автомобиля на линию α_в. Коэффициент технической готовности идентичен коэффициенту технического использования, являющемуся комплексным показателем надежности, Один из вариантов формулы для расчета К_Τ.Γ следующий:

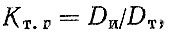
где D_и - количество дней, в которые автомобиль был технически исправен; D_T - общее количество календарных дней, в течении которых определялся искомый показатель.

Другой вариант выражения для К_{т. г}, аналогичный K_Γ:

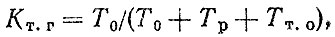
где Т_р - среднее время простоя в ремонтах (плановых к внеплановых); T_T.O - среднее время простоя в техническом обслуживании.

Коэффициент выпуска на линию характеризует годовой пробег автомобиля и, следовательно, его производительность:

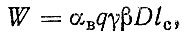
где W - производительность автомобиля, тыс, км; q - грузоподъемность автомобиля, т; γ - коэффициент использования грузоподъемности; р - коэффициент использования пробега D - количество календарных дней в году (365 дн.); 10 - среднесуточный пробег автомобиля, км/день.

Коэффициент α_в зависит от целодневных простоев не только по техническим, но и по организационным причинам, и для оценки эффективности проектируемой конструкции необходимо располагать его прогнозными значениями.

Расчет К_{т. г} к α_в в зависимости от наработки с начала эксплуатации или срока службы производится по данным наблюдений за подконтрольными партиями автомобилей.

Для прогнозирования комплексных показателей надежности автомобиля можно воспользоваться марковскими дискретными случайными процессами с непрерывным временем с помощью которых вероятности состояний Р_i(L) автомобиля описываются в виде системы дифференциальных уравнений, На стадии проектирования целесообразно ограничить число возможных состояний и учитывать только основные интенсивности переходов. Тогда система уравнений записывается в виде

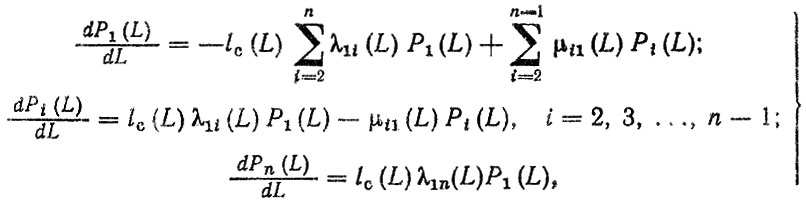(3.71)

где P_i(L) - вероятность нахождения автомобиля в i-м состоянии (Р_i(L) - автомобиль исправен, работает; Р_п (L) - автомобиль списывается); λ_1i(L) - интенсивность перехода из первого в i-e состояние (отказы); μ_i1(L) - интенсивность перехода из i-го в первое состояние (восстановление); l_с (L) - средний пробег.

Анализ показал, что в расчетную модель следует включить следующие вероятности состояний автомобиля (рис. 3.8): Р₁(L) - исправен, работает на линии; Р₂ (L) - проходит техническое обслуживание; Р₃ (L) - находится в текущем ремонте; Р₄ (L) - отправлен в капитальный ремонт; Р₅ (L) - исправен, простаивает по организационным причинам Р₆ (L) - списывается.

Система уравнений (3.71) характеризуется следующими особенностями.

1. Учитываются интенсивности перехода, связывающие первое состояние (исправен) с остальными, что позволяет существенно упростить сбор и систематизацию необходимой информации.

2. Поскольку большинство интенсивностей переходов λ_ij(L) зависит от пробега (времени), то система решается численными методами.

3. Техническое обслуживание учитывается только такое, которое приводит к целодневным простоям. Например, для грузовых автомобилей - это техническое обслуживание ГО-2 и сезонное обслуживание. Проведенные исследования показали, что периодичность ТО-2 подчиняется нормальному закону с параметрами: среднее значение L, тыс. км; среднее квадратическое отклонение ст, тыс. км. Интенсивность перехода "исправен-техническое обслуживание" рассчитывается по формуле

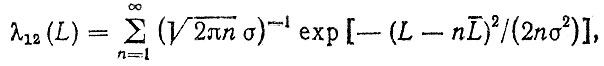(3.72)

где n - порядковый номер ТО-2.

На стадии проектирования для оценки λ₁₂ (L) можно воспользоваться асимптотической формулой для простого процесса восстановления [см. формулу (3,18)], т. е, упрощенной оценкой λ₁₂ = L^-1.

4. Интенсивность перехода λ₁₃ (L) "исправлен-текущий ремонт" определяется в виде суммы параметров потоков отказов

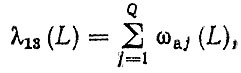(3.73)

где ω_{а j} (L) - параметр потока отказов j-го агрегата (системы); Q - число агрегатов, требующих разборки (или снятия с автомобиля) для замены отказавшей детали.

При формировании потока отказов ω_{a j} (L) [см, формулу (3.43)] учитываются главным образом детали, требующие разборки агрегата, На стадии проектирования к ним в первую очередь могут быть отнесены детали, лимитирующие надежность.

При расчетах λ₁₃ (L) аппроксимируется каким-либо аналитическим выражением.

Таким образом, состояние автомобиля "текущий ремонт" означаем что из различных по продолжительности текущих ремонтов учитываются те, которые приводят к цело-дневным простоям автомобиля и не могут быть выполнены в межсменное время. Цело-дневные простои связаны с текущим ремонтом таких агрегатов, как двигатель, сцепление, коробка передач, главная передача,

5. Интенсивность перехода λ₁₄ (L) "исправен-капитальный ремонт" будет зависеть от числа М планируемых капитальных ремонтов за период эксплуатации до списания автомобиля

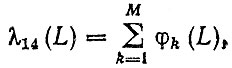(3.74)

где φ_k(L) - плотность распределения ресурса автомобиля до k-го ремонта,

6. Состояние "исправен, не работает" означает простой технически исправного автомобиля по различным причинам: выходные и праздничные дни, отсутствие клиентуры, бездорожье, необеспеченность водителями и др. На стадии проектирования целесообразно учитывать только простои, связанные с выходными днями.

7. Интенсивность перехода λ₁₆ (L) "исправен-списывается" будет определяться интенсивностью отказов функции распределения ресурса до описания

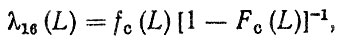(3.75)

где f_с (L), F₀ (L) - соответственно плотность и функция распределения ресурса автомобиля до списания.

8. Интенсивности переходов μ_i1 (L) при расчетах на стадии проектирования могут быть приняты постоянными, равными обратным средним величинам соответствующих воздействий, связанных а восстановлением

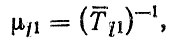(3.76)

где Т_j1 - среднее время проведения j-го ремонтного воздействия (или простоя),

9. При λ_1i(L) = μ_j1 (L) = const и исключении вероятности списания Р₆ (L) система уравнений (3,71) при L → ∞ позволяет получить оценки комплексных показателей надежности автомобиля для стационарного режима. Так" вероятность исправной работы - коэффициент выпуска - рассчитывается по формуле

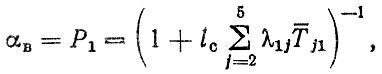(3.77)

коэффициент технической готовности

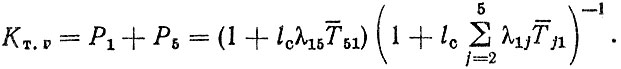(3.78)

Основным недостатком формул (3.77), (3.78) является независимость вероятности состояний от наработки и, следовательно" невозможности оптимизации по ресурсу или сроку службы.

Для примера рассчитаем коэффициенты α_в и К_{T. Г} для грузового автомобиля средней грузоподъемности. Исходные данные для расчета приведены в табл. 3.15. Для определения λ₁₃ (L) были смоделированы потоки отказов по 37 деталям, лимитирующим надежность, из них по двигателю - 12 деталей, по сцеплению - 5, по коробке передач - 11, по ведущему мосту - 9 деталей. При расчете ₁₄ (L) учитывались два капитальных ремонта, каждый из которых подчиняется нормальному закону. Интенсивности λ₁₃ (L) и λ₁₄(L) были откорректированы с учетом списания (для исключения последействия).

На рис. 3.9 приведены интенсивности отказов (L) и результаты расчетов системы методом Рунге-Кутта. В частности, для λ₁₃ (L) была подобрана аппроксимирующая зависимость в виде полинома второго порядка и экспоненты. Из рисунка видно, что коэффициенты α_в, K_Τ.Γ уменьшаются с увеличением пробега автомобиля максимумы на пробеге 220-300 тыс. км объясняются влиянием капитальных ремонтов автомобилей.

Таблица 3.15. интенсивности λ_1i и μ_i1 (для расчета комплексных показателей надежности)

Для агрегатов -с помощью системы уравнений, аналогично (3.71) , можно рассчитать коэффициенты технической готовности. При этом необходимо выделить соответствующие вероятности состояний нахождения автомобиля в текущем ремонте, связанные с отказом деталей конкретного агрегата. Интенсивности переходов для агрегатов рассчитываются на основании параметров потоков отказов деталей [см. формулу (3.73)].

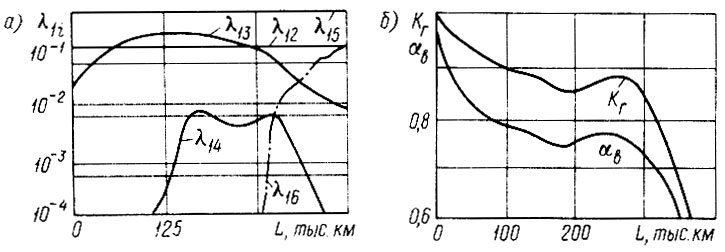
Рис. 3.9. Определение комплексных показателей надежности автомобиля: а - интенсивности переходов из исправного в г-е состояние; б - зависимости коэффициентов технической готовности k_г и выпуска α_в от пробега

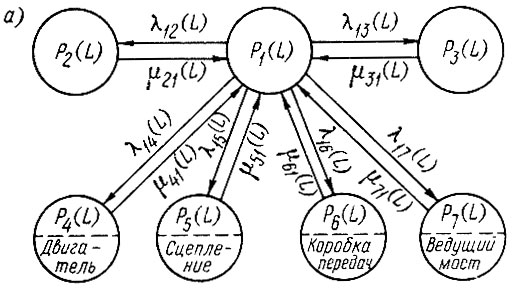
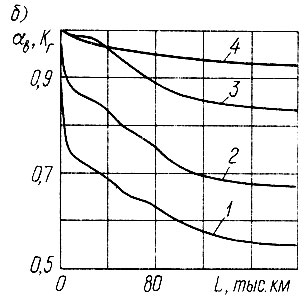
Рис. 3.10. Комплексные показатели надежности агрегатов и автомобиля: а - граф состояний автомобиля; б - коэффициенты выпуска автомобиля (1) и технической готовности автомобиля (2), двигателя (3), коробки передач (4)

Рассмотрим пример расчета коэффициентов технической готовности агрегатов. На рис. ЗЛО, а приведен граф состояния автомобиля, включающий: Р₁(L) - автомобиль исправлен, работает; Р₂ (L) - проходит ТО-2; P₃(L) - Р₃ (L) - исправлен, простаивает; P₄ (L),..., Р₇ (L) - находится в текущем ремонте, связанном соответственно с ремонтом двигателя, сцепления, коробки передач и ведущего моста" Система уравнений запишется в виде

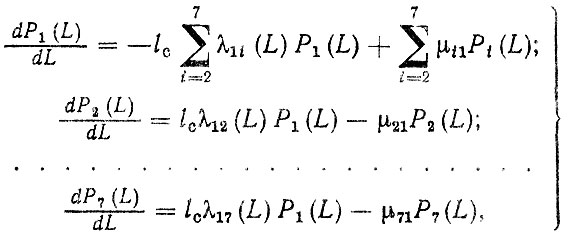(3.79)

где λ₁₂ = 0,1; λ₁₃ = 0,8; λ₁₄ (L) = -0,374 + 0,016 L - 4,4 × 10^-5L² при L > 30 тыс. км; λ₁₅(L) - 0,55 - 0,2/(L + 1); λ₁₆(L) = -0,021 + 0,0311 - 3,7 × 10^-6L²; λ₁₇ (L) = 0,036 + 0,028L - 7,7×10^-6L²; μ₂₁,...,μ₇₁ = 1 (размерность λ - отказ/тыс. км; (μ - восст./день); l_c = 0,25 тыс. км/день.

Тогда коэффициент готовности автомобиля

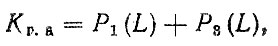
коэффициент готовности двигателя

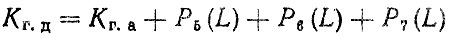
и т. д. (рис. 3.10, б).

Очевидно, К_{г. а} < К_Γi где K_Γi - коэффициент готовности г-го агрегата.

Рассчитаем коэффициент выпуска α_B, коэффициенты готовности автомобиля и агрегатов для стационарного режима. Для системы (3.79)

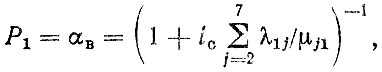
а вероятность нахождения в состоянии Р_i равна

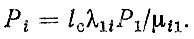
При ₁₄ = 0,1; λ₁₅ = 0,04; λ₁₆ = 0,025; λ₁₇ = 0,035 имеем α_B = Р₁ = 0,784; К_{г. а} = P₁ + P₃ = 0,941; К_Γ.Д = 0,960; К_Γ.ΚΠ = 0,972; К_{г. кп} = 0,974; К_Г.M = 0,976.

Вышеизложенное может быть представлено в виде блок-схемы методики расчета (прогнозирования) показателей надежности деталей и агрегатов автомобиля (рис. 3.11) на этапе проектирования. Проведение расчетов в соответствии с блок-схемой является первым этапом, который можно сравнить с принятым в практике конструирования проектным расчетом автомобиля. Результаты расчета используются для принятия управленческих решений, связанных с разработкой организационно-технических мероприятий и направленных на достижение заданных показателей надежности и их оптимизацию.

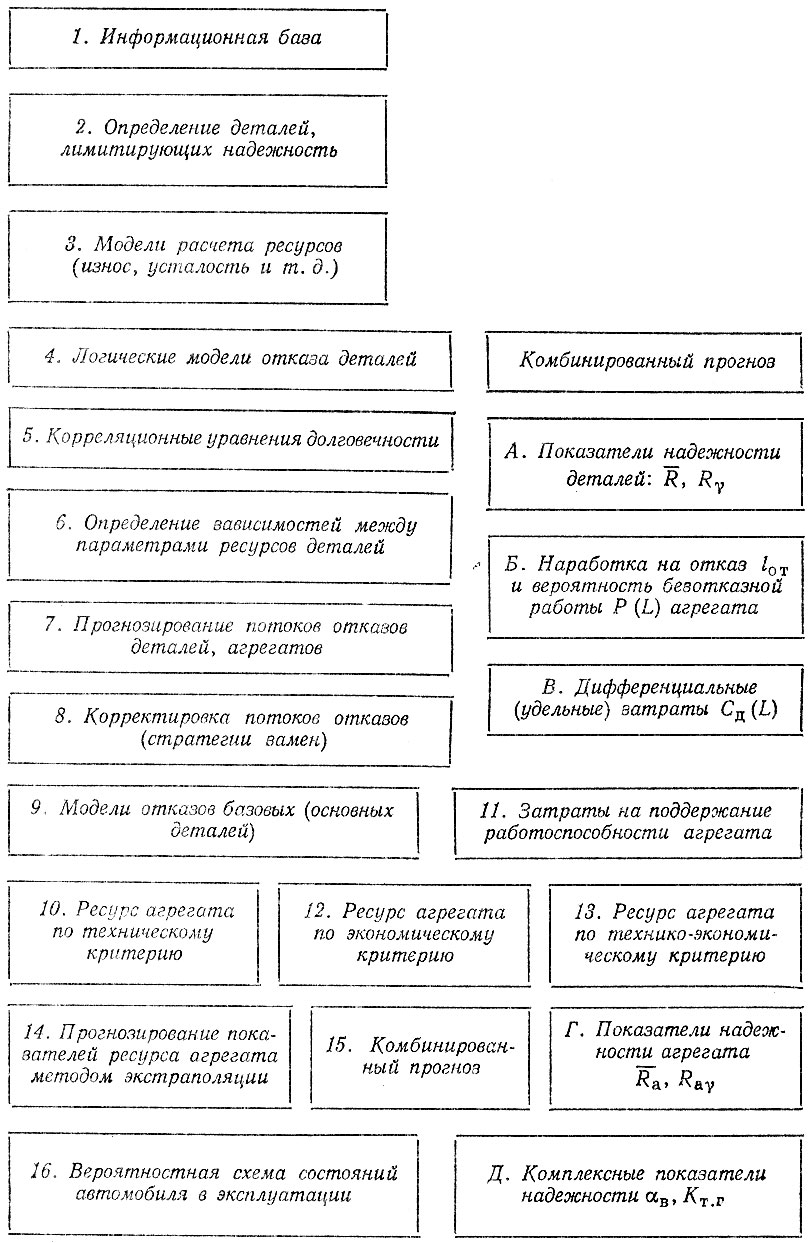
Рис. 3.11. Блок-схема прогнозирования показателей надежности деталей и агрегатов автомобиля