
3.4. Расчет единичных показателей надежности агрегатов автомобиля
На основании параметров потоков отказов рассчитываются следующие показатели надежности агрегата: вероятность безотказной работы Р (L); наработка на отказ lOT(L); переменные затраты на поддержание агрегата в работоспособном состоянии; параметры ресурса до капитального и между капитальными ремонтами и комплексные показатели в частности, коэффициент технической готовности.
Вероятность безотказной работы и наработки на отказ. Для восстанавливаемых объектов Р (L) определяется по формуле
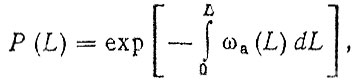 (3.52)
(3.52)где ωа (L) - откорректированный параметр потока отказов агрегата.
Известно что суммирование достаточно большого числа случайных потоков при определенных условиях приводит к пуассоновскому потоку при котором промежутки времени между двумя соседними отказами подчиняются экспоненциальному распределению. Так как ωа (L) зависит от пробега, то лишь для отдельных интервалов ΔLi можно принять ωa(ΔLi) = ωai = const, Тогда вероятность безотказной работы агрегата на интервале
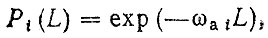 (3.53)
(3.53)а средняя наработка на отказ
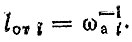 (3.54)
(3.54)Переменные затраты на текущий ремонт. Переменные затраты на текущий ремонт агрегата включают затраты на запасные части, трудовые затраты и материалы и могут быть выражены в виде удельных (дифференциальных) Сд (L) или суммарных CΣ (L) затрат
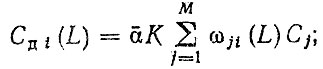 (3.55)
(3.55)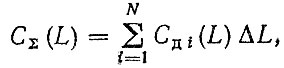 (3.56)
(3.56)где ωji (L) - откорректированный e учетом стратегии замен и корреляции параметр потока отказов j-й детали на t-ом интервале пробега; Cj - оптовая цена j-ой детали; М - число деталей, лимитирующих надежность агрегата; α - коэффициент [см. (3.43)]; К - коэффициент, учитывающий соотношение между затратами на запасные части и другими затратами при текущем ремонте (трудовые затраты и материалы).
Коэффициент К введен по аналогии с предложенным в работах [66, 75 3 для автомобиля в целом и включающим помимо перечисленных затрат компенсацию простоев автомобиля,
В целях прогноза коэффициентов К были выполнены расчеты для грузовых автомобилей с учетом года начала выпуска Т и общей массы Q (табл, (ЗЛО). Исходные данные для расчетов, включающие затраты на запасные части, трудовые затраты и материалы, взяты из справочной литературы. Из анализа полученных зависимостей следует, что наблюдается устойчивая тенденция снижения коэффициентов К в зависимости от T и Q. Заметим, что нормативные данные для составляющих затрат приводятся для автомобиля в целом, поэтому при прогнозных расчетах делается допущение о возможности использования полученных зависимостей для отдельных агрегатов, По мере накопления информации для новых автомобилей составляющие затрат должны уточняться.

Таблица 3.10. Коэффициенты учета составляющих затрат при текущем ремонте К (для грузовых бортовых автомобилей общего назначения)
Входящие в формулу (3.55) оптовые цены деталей для проектируемого автомобиля определяются следующим образом: по аналогии с ранее выпущенными моделями, по результатам экспертного опроса или на основе калькуляции себестоимости и перехода к оптовой цене G использованием зависимостей, подробно рассмотренных в работе [26].
Уточним понятия удельных и дифференциальных затрат, определяемых в результате деления цены (или другого показателя) на пробег автомобиля и имеющих размерность руб./тыс. км. Если при расчетах деление производится на интервал пробега автомобиля ΔL, то такие затраты следует считать дифференциальными (либо они могут быть получены на основе дифференциальных зависимостей, например, с помощью параметра потока отказов). Если деление производится на пробег автомобиля L, то затраты будем относить к удельным" Следует заметить, что удельные и дифференциальные затраты тождественны только в случае линейных зависимостей нарастания показателя, так как операции деления и дифференцирования дают одинаковый результат.
Показатели ресурса агрегата. Согласно "Положению" [53], агрегат направляется в капитальный ремонт, если базовая и основные детали нуждаются в ремонте, требующем полной разборки агрегата; работоспособность не может быть восстановлена или ее восстановление экономически нецелесообразно путем проведения текущих ремонтов. Следовательно, критерий постановки агрегата в капитальный ремонт является технико-экономическим, а случайная величина ресурса до капитального ремонта может быть представлена в виде
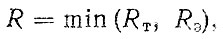 (3.57)
(3.57)где RT, RЭ - случайные величины ресурсов агрегата по техническому и экономическому критериям.
Функция распределения ресурса агрегата до капитального ремонта Fa (R), с помощью которой определяются средний и гамма-процентный ресурсы, рассчитывается по формулам для минимальных значений (табл. 2,2), на основе функций распределений ресурсов по техническому FT (R) и экономическому FЭ(R) критериям
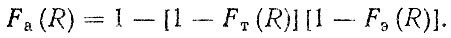 (3.58)
(3.58)
Ресурс агрегата по техническому критерию. Для нахождения расчетным путем необходимо построить логическую модель ресурса базовой детали, включающую выявление основных сечений, например, с использованием дефектных ведомостей на капитальный ремонт аналогичных конструкций, а также определение видов и параметров разрушительных процессов и предельных состояний. Однако несмотря на теоретически ясную постановку задачи в настоящее время отсутствуют не только методики прогнозных расчетов ресурсов базовых деталей по техническому критерию, но они не выполняются и для существующих конструкций. Поэтому оценка, как правило, производится по результатам испытаний. Это объясняется многими причинами, главные из которых следующие:
отсутствие точных критериев предельных состояний (кроме явных случаев разрушения в виде трещин, пробоин, сколов);
трудность учета влияния изменения размеров (геометрии) сечений базовых деталей (износы, деформации, нарушение соосности отверстий и т. д.) на нагрузочные режимы и предельные состояния остальных деталей агрегата, т. е. на их ресурсы;
необходимость определения большого количества исходных данных для описания разрушительных процессов, протекающих в сечениях базовых деталей, их взаимосвязь (коррелируемость) одновременное приложение растягивающих (сжимающих) нагрузок, изгибающих и крутящих моментов, представляющих нестационарные случайные процессы, а также остаточные напряжения и т. п.
Следует заметить, что использование методов конечных элементов (МКЭ) позволяет решить часть, проблемы расчета ресурсов базовых деталей, связанной, главным образом, с оценкой статической и усталостной прочности, в частности, возникновением и развитием трещин.
Рассмотрим пример расчета ресурса коробки передач по условному техническому критерию - достижению диаметрами отверстий картера под подшипники валов размеров "допустимых без ремонта". Исходные данные и результаты расчетов приведены в табл. 3.11; скорости изнашивания определены с помощью микро-метрирования. Расчеты средних Li и средних квадратических отклонений σi наработок до предельного состояния для каждого диаметра отверстия (сечения) производились по формулам:

где δрi - расчетный допустимый износ i-го диаметра; δoi - среднее начальное значение i-го диаметра; ui, σui - среднее и среднее квадратическое отклонения скорости изнашивания i-го диаметра, Допустив, что средний ресурс по техническому критерию определяется средними значениями ресурсов по каждому сечению, находим
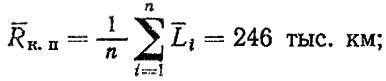
аналогично, для среднего квадратического отклонения
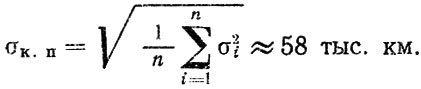
Таким образом, можно принять, что ресурс коробки передач по условному техническому критерию подчиняется нормальному закону распределения
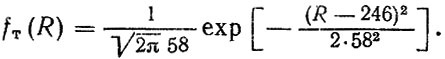
Гамма-процентный ресурс Rγ=90 = 170 тыс. км.
Ресурс агрегата по экономическому критерию. По аналогии s автомобилем под ресурсом агрегата до капитального ремонта по экономическому критерию будем понимать такой ресурс RЭ, при котором достигается минимум удельных затрат на приобретение и поддержание его в работоспособном состоянии
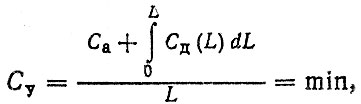 (3.59)
(3.59)
где Са - оптовая цена агрегата" руб." Сд (L) - дифференциальные затраты на текущий ремонт агрегата [формула (3.55)].
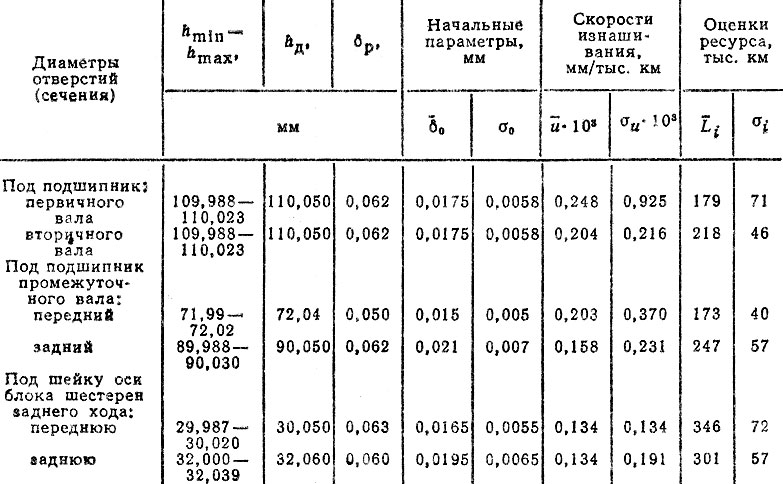
Таблица 3.11. Определение ресурса коробки передач с учетом износа отверстий картера (технический критерий)
Определение ресурса агрегата RЭ по критерию минимума удельных затрат можно считать задачей локальной (внутренней) оптимизации, которая в случае сохранения граничных условий и целей, не противоречит глобальной оптимизации, т. е. определению оптимального ресурса автомобиля, В общем случае необходимо рас-смотреть общую задачу оптимизации ресурсов автомобиля и агрегатов с учетом их капитальных ремонтов. Расчет ресурса RЭ не
вызывает затруднений при наличии информации о затратах на текущие ремонты агрегатов эксплуатировавшихся автомобилей на пробегах, превышающих RЭ. При прогнозировании решение задачи усложняется и становится многовариантным по следующим причинам:
возможность выбора в качестве основной расчетной зависимости дифференциальных или суммарных затрат и, соответственно, различных аппроксимирующих функций (параболы, степенной, экспоненциальной и т. п.);
изменение коэффициентов аппроксимирующих функций в зависимости от величины пред прогнозного периода (числа учитываемых точек), что приводит и к различным прогнозным оценкам RЭ.
Для примера в табл. 3.12 приведены дифференциальные и суммарные затраты, связанные с заменой десяти деталей коробки передач и определенные на основе смоделированных потоков отказов (до третьего отказа включительно). Результатырасчетов ресурсов по экономическому критерию для степенной и экспоненциальной зависимостей и для различных величин предпрогнозных периодов даны в табл. 3,13, из анализа которой следует:
оценки RЭ существенно различаются и составляют от ПО до 406 тыс. км;
для прогнозных расчетов следует выбрать степенную зависимость как наиболее достоверную по величине корреляционного отношения η;
вычислительные операции, связанные с определением RЭ по формуле (3.59) по дифференциальным и суммарным затратам на основе экспериментальных или смоделированных данных, неадекватны; учитывая их достоверность (по корреляционному отношению η), целесообразно рассчитывать RЭ по формуле
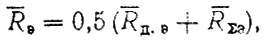
где RД.Э., RΣЭ - соответственно оценки ресурсов с использованием дифференциальных и суммарных затрат.
Например, для степенной зависимости при использовании для аппроксимации N = 6 точек находим RЭ = 327 тыс. км; при N = 12 RЭ = 340 тыс. км.
Для уменьшения разброса прогнозных оценок RЭ в некоторых случаях полезно увеличить число моделируемых отказов и объем выборки.
Изложенная методика прогноза оптимального ресурса RЭ требует расчета потоков отказов деталей, которые, в свою очередь, предполагают наличие законов распределения ресурсов деталей до первого и последующего отказов.
В то же время представляет интерес разработка такой методики оценки оптимального ресурса, которая включает минимальный объем информации, например только данные о средних ресурсах деталей, лимитирующих надежность до первого отказа. Очевидно такой вариант должен базироваться на асимптотических формулах для общего процесса восстановления и корреляционных зависимостях между параметрами ресурсов деталей. Рассмотрим последовательность расчетов по предлагаемой методике.
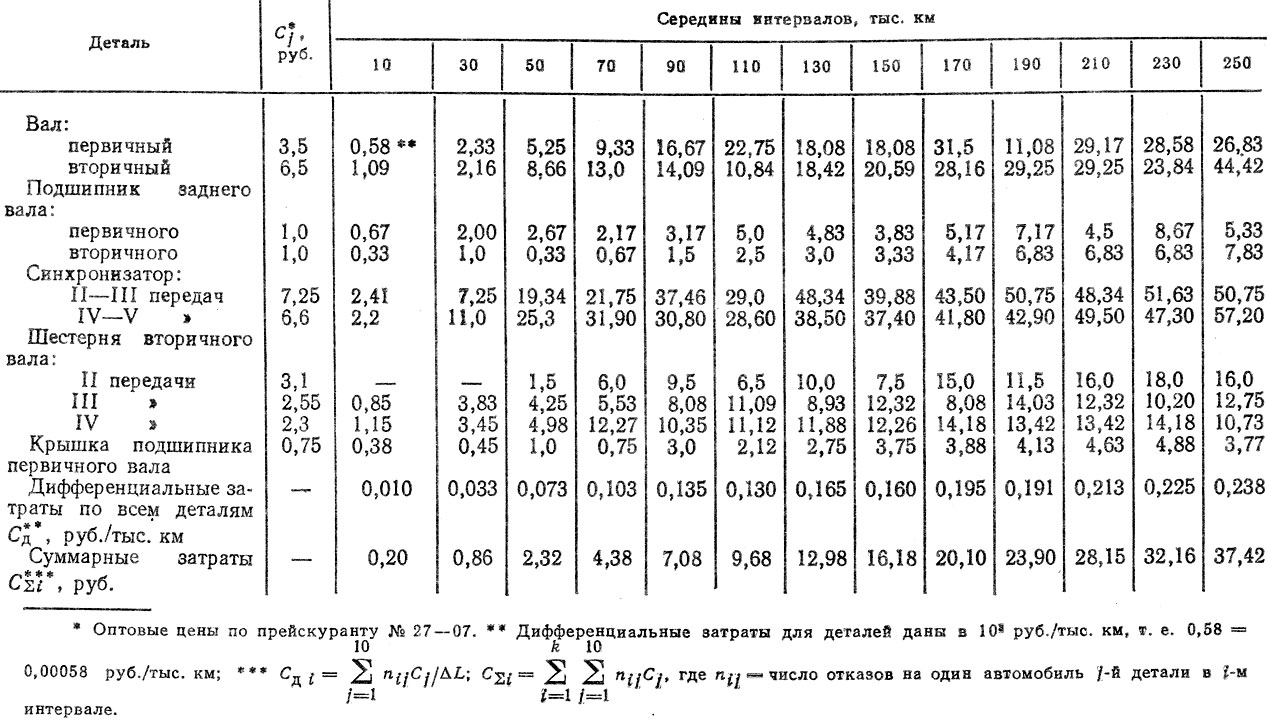
Таблица 3.12. Определение дифференциальных и суммарных затрат на запасные части коробки передач (на один автомобиль)
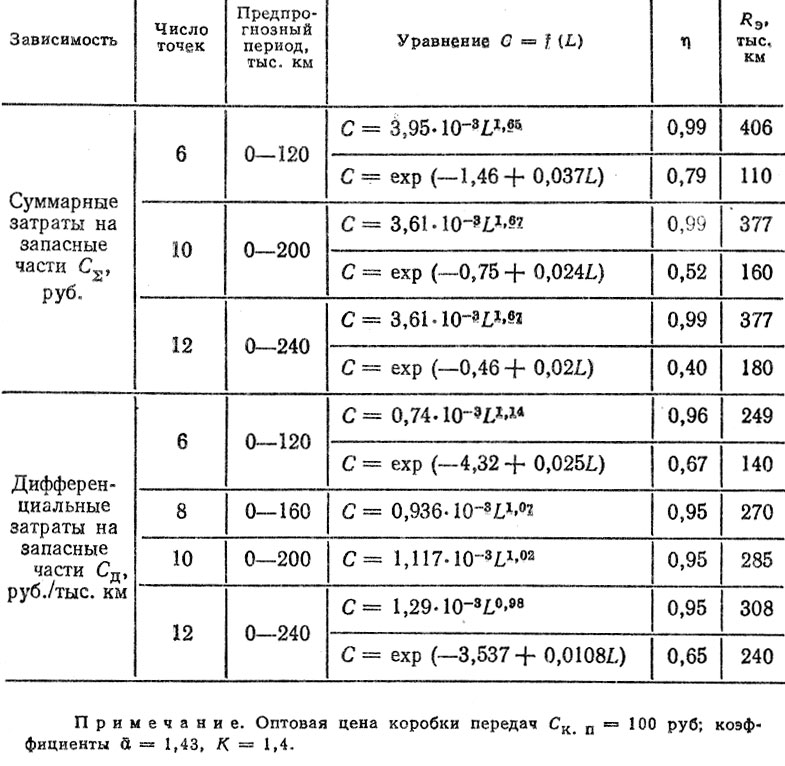
Таблица 3.13. Расчет ресурсов коробки передач но экономическому критерию
1. Для агрегата" включающего М деталей" критических по надежности, определяется средний ресурс до первого отказа
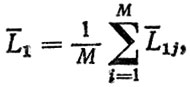 (3.60)
(3.60)где L1j - средний ресурс j-й детали до первого отказа.
2. По оптовым ценам Cj определяются среднее значение С и среднее квадратическое отклонение аσcстоимости "осредненной" детали
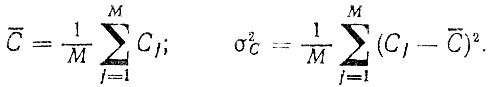 (3.61)
(3.61)3. По корреляционным зависимостям между параметрами ресурсов деталей находятся:
среднее квадратическое отклонение ресурса σ1 до первого отказа
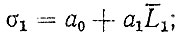
средний ресурс L1,2 и среднее квадратическое отклонение ресурса σ1,2, а между отказами:
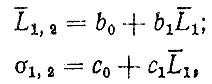
где L1 - по формуле (3.60).
4. С использованием соотношений для общего процесса восстановления [формула (3,17)] записываются формулы для ведущей функции потока затрат на запасные части
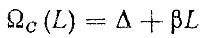 (3.62)
(3.62)
и длины (абсциссы) переходного процесса [формула (3,20)]
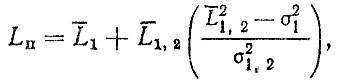 (3.63)
(3.63)
где
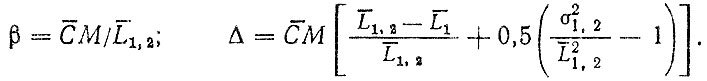
5. Если уравнение для суммарных (накопленных) затрат на запасные части выбрано в виде степенной функции
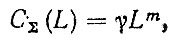 (3.64)
(3.64)
то коэффициенты γ и m находятся из системы уравнений
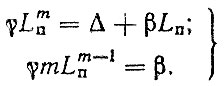 (3.65)
(3.65)Первое уравнение получено исходя из условия, что кривая СΣ(L) (рис. 3,7) проходит через точку с координатами (СΣ (LΠ), L = LΠ); второе уравнение - из условия, что кривая CΣ(L) является касательной к асимптотической прямой Ωc (L) [формула (3.62)] в точке LΠ.
6. Из решения системы (3.65) находим:
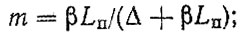 (3.66)
(3.66)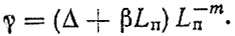 (3.67)
(3.67)
Тогда, при подстановке (3.64), (3.66), (3.67) в общую формулу (3.59) и соответствующих преобразований, связанных с определением минимума, получим выражение для оптимального среднего ресурса
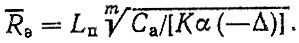 (3.68)
(3.68)
7. Для нахождения оценки среднего квадратического отклонения ресурса воспользуемся формулой
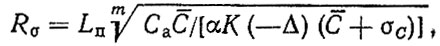
(3.69)
где - оценка ресурса, соответствующая ведущей функции потока затрат, [формула (3.62)], домноженной на
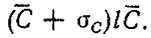
Следовательно, в первом приближении среднее квадратическое отклонение ресурса агрегата
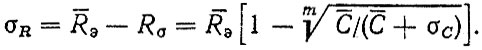 (3.70)
(3.70)
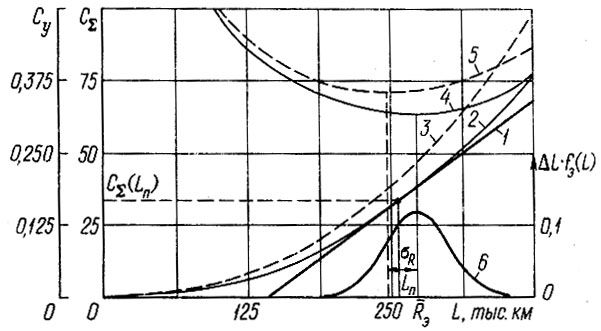
Рис. 3.7. Определение показателей ресурса агрегата до капитального ремонта по экономическому критерию: 1 - асимптотическая зависимость средних затрат Ωc (L); 2 - средние затраты на запасные части СΣ(L); 3 - затраты СΣ (L) с учетом σс; 4 - суммарные средние удельные затраты; 5 - то же с учетом σc; 6 - распределение ресурса агрегата
Таким образом, предлагаемая методика позволяет оценить не только средние, но и средние квадратические отклонения ресурсов агрегатов по экономическому критерию без трудоемкого процесса моделирования потоков отказов деталей.
Пример. Рассчитаем показатели оптимального ресурса автомобильного двигателя, исходные данные о средних ресурсах деталей которого приведены в табл. 3.14 [17]; там же даны оптовые цены, выбранные, в основном, согласно прейскуранту № 27-07. По формуле (3.80) находим (при М = 8) средний ресурс L1 = 155,8 тыс. км, а также стоимостные показатели С = 18,1 руб.; σc = 16,53 руб. С помощью корреляционных зависимостей, приведенных в п. 3.1, получим σ1 = 12 + 0,26L1 = 52,5 тыс., км; L1,2 = 3 + 0,46L1 = 70 тыс. км; σ1,2 = 5 + 0,31L1 = 53,3 тыс. км.
По формулам (3.62) и (3.63) находим Ωc (L) = -155,9 + 1,55L, LΠ = 208,6 тыс. км и коэффициенты степенной зависимости [формулы (3.66), (3.67)] m = 1,41, γ = руб.⋅(тыс. км)-1,41.
Для расчета показателей оптимального ресурса принимаем оптовую цену двигателя С0 = 500 руб., коэффициенты α = 1,43; К = 1,5. Тогда при подстановке значений в формулы (3.68) и (3.70) находим, что RЭ = 277 тыс. км, σR = = 102 тыс. км.
Для сопоставления показателей оптимальных ресурсов агрегатов по предлагаемой методике и методике, основанной на моделировании потоков отказов деталей, были выполнены расчеты для двигателя автомобиля ГA3-53 А и коробки передач автомобиля ЗИЛ-130 (исходные данные для расчета коробки передач см. в табл. 3.12). Средний ресурс L1 = 253 тыс. км, средняя стоимость одной детали С = 3,5 руб., σс = 1,0 руб. По формулам (см. табл. 3.4) σ1 = 0,47L1, L1,2 = 0,48L1, σ1,2 = 14 + 0,37L1; тогда Ωc (L) = -41,5 + 0,29L; LΠ = 253 тыс. км; коэффициенты степенной зависимости m = 2,33, γ = 0,805 × 10-4 руб. (тыс. км)-2,33. Показатели оптимального ресурса коробки передач при Ск. п = 100 руб. ; α = 1,43; К = 1,4 равны RЭ = 274 тыс. км, σR = 28 тыс. км. Средний ресурс по результатам моделирования потоков отказов детали, приведенных в табл. 3.12, до третьего отказа включительно, составил RM = 327÷340 тыс. км.
Аналогичные расчеты для двигателя автомобиля ВАЗ-53А (по данным, приведенным в работе 139]) позволили определить RЭ = 193 тыс. км; σR =115 тыс. км; средний ресурс по результатам моделирования RM = 170 тыс. км.
Таким образом, по двигателю наблюдается хорошее совпадение оценок средних ресурсов при расчетах по обеим методикам; различие оценок средних ресурсов для коробки передач по результатам моделирования и с использованием асимптотических соотношений объясняется, в частности, тем, что смоделированный с учетом трех отказов деталей поток не достиг насыщения.
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'