
3.3. Прогнозирование потоков отказов агрегатов автомобиля
В работах [24, 36, 75] подробно описана методика и даны примеры расчетов потоков отказов агрегатов автомобиля на основании результатов наблюдений за подконтрольными партиями автомобилей в ЭПАХах, ОАТП и рядовых АТП. Параметр потока отказа агрегата по интервалам пробега определяется по формуле
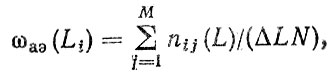 (3.39)
(3.39)где nij - число отказов j-й детали агрегата в i-м интервале пробега; М - число деталей агрегата, у которых зафиксированы отказы; ΔL - интервал пробега, тыс. км; N - число агрегатов подконтрольной партии.
Основное преимущество потока отказов агрегата, определяемого по экспериментальным данным, заключается в том, что в нем учитываются отказы всех деталей и их "множественность", т. е. одновременная замена нескольких деталей" а также взаимосвязь (корреляция) параметров наработок до первого и последующих отказов как для каждой детали, так и между деталями агрегата (если она имеется)* Таким образом, при прогнозировании потока отказов агрегата необходимо учитывать указанные особенности формирования эксплуатационного потока.
Рассмотрим вначале последовательность расчета (прогноза) потока отказов агрегата без учета множественности отказов и корреляции. Очевидно, по аналогии о формулой (3.39) можно записать
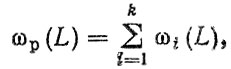 (3.40)
(3.40)
где ωi(L) - расчетный параметр потока отказов 1-й детали; k - число учитываемых деталей.
Из анализа табл. 3.3 следует, что параметры распределений ресурсов между первым и вторым отказами (L1,2, σ1,2) и вторым и третьим отказами (L2,3, σ2,3) имеют близкие значения. Поэтому при отсутствии точной информации для прогнозирования потоков отказов на этапе проектирования можно ограничиться рассмотрением общего процесса восстановления. При этом возможны два варианта: первый - ресурс до первого отказа подчиняется нормальному закону, а последующие отказы (между первым и вторым и т. д.) - распределению Вейбулла; второй - ресурсы до первого отказа и между отказами подчиняются распределению Вейбулла, но параметры этих распределений различны. В этом случае удается существенно упростить алгоритм расчета на ЭВМ.
Допустим, что с помощью моделей ресурса и синтеза прогнозов получен, по крайней мере, один параметр - средний ресурс t-й детали до первого отказа. Дальнейшие этапы расчета следующие.
1. По корреляционным зависимостям (табл. 3.3-3.5) определяются значения среднего квадратического отклонения σ1 и коэффициента вариации υ1 с помощью которого находится второе значение σ'1 = υ1L1. По значениям σ'1 и σ1 в виде среднего или средневзвешенного значения определяется расчетное значение σ1* (весовые коэффициенты могут быть приняты пропорциональными величинам корреляционных отношений для зависимостей σ1 от L1 и υ1 от L1).
2. На основании накопленного опыта статистической обработки или теоретических положений выбирается закон распределения ресурса детали. Если закон распределения неизвестен, то при прогнозировании он может быть выбран на основании L1 и σ*1. Поскольку ресурсы деталей являются положительными величинами, то можно принять, что при σ*1 > 0,33L1 распределение подчиняется закону Вейбулла (В), а при σ1 < 0,33L1 - нормальному закону (Н). Например, прямая О А на рис, 3.3, б разграничивает области указанных законов распределения.
При необходимости более точного определения вида закона распределения можно воспользоваться рекомендациями работы [36], в частности, при υ = 0,52 - закон Рэлея, υ = 0,65 - логарифмически нормальный закон, υ = 1 - экспоненциальный. Но если отказ вызван износом или усталостью, то при υ = 1 следует использовать логарифмически нормальный закон [34].
3. Параметр распределения Вейбулла m находится по коэффициенту вариации υ1 = σ*1/L1 с помощью таблицы или графика [413. Второй параметр рассчитывается по формуле L0 = L1/bm, в которой коэффициент bm определяется по тем же таблицам или графикам, что и параметр m, либо с помощью гамма-функции: bm = Г (1 + 1/m).
4 Рассчитываются L1,2 и σ*1,2 между первым и вторым отказом при этом σ*1,2 находится как среднее или средневзвешенное значение по σ1,2 от L1 и σ'1,2 от L1,2. По найденным величинам выбираются законы и их параметры также, как для первого отказа.
Следует заметить, что при наличии корреляционных уравнений аналогичные расчеты могут быть выполнены и для последующих отказов, т. е. для L2, з" 02, з и т. д. Помимо этого, если получена плотность распределения ресурса до первого отказа и, соответственно, L2,3, σ*2,3, то расчет начинается с этапа 4.
5. На основании f1(L) и f1,2 (L) рассчитываются плотности распределения (гистограммы) ресурсов деталей до второго f2 (L) и последующих отказов, суммирование которых по интервалам пробега позволяет получить параметр потока отказов i-й детали ωi (L).
По вышеизложенной методике были выполнены расчеты потоков отказов для деталей агрегатов автомобиля. Результаты расчета параметров и выбранные законы распределения до первого и между последующими отказами приведены в табл. 3.7, Там же даны фактические параметры ресурсов. При расчете параметров по корреляционным зависимостям величина среднего ресурса L1 принималась равной фактическому среднему ресурсу до первого отказа. По фактическим и расчетным данным с помощью метода Монте-Карло были смоделированы потоки, включавшие первый, второй и третий отказы. Объем выборки для каждой реализации был выбран равным 900, т. е. наработки на каждый отказ моделировались в объеме N = 300. На рис. 3.4 приведены параметры потоков отказов, рассчитанные по формуле
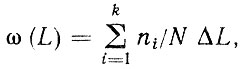 (3.41)
(3.41)
где ni - суммарное число первых, вторых и третьих отказов детали в i-м интервале; k - число интервалов.
Поскольку в литературе не удалось встретить критериев или оценок для сопоставления потоков отказов (подобных, например, критериям Пирсона или Колмогорова для функций распределения), то расхождение между потоками оценивалось с помощью коэффициента
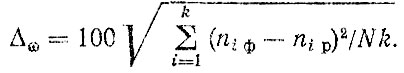 (3.42)
(3.42)Индексами "ф" и "р" обозначены соответственно числа отказов, смоделированных по фактическим и расчетным данным. Результаты расчетов и ошибок параметров распределений [см, формулу (3.3)] приведены в табл. 3.8.
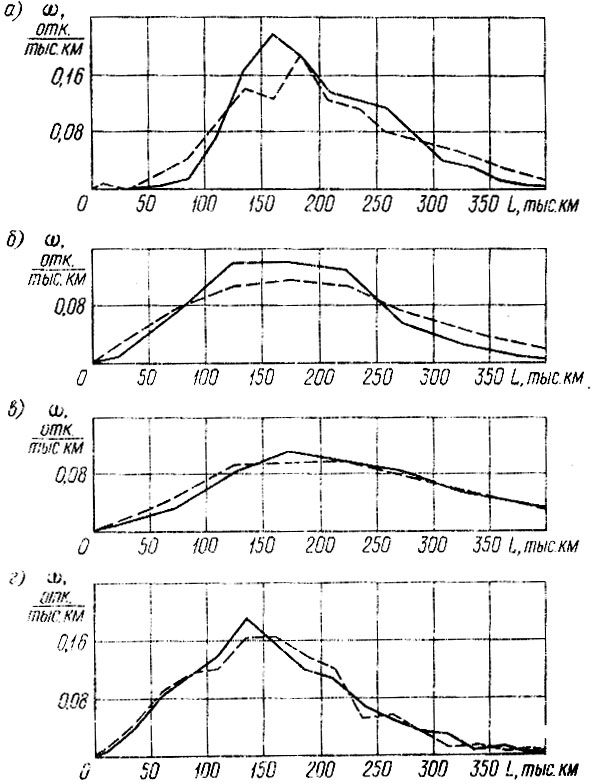
Рис. 3.4. Параметры потоков отказов деталей, включающие первый, второй и третий отказы, для агрегатов автомобиля: а - двигатель; б - сцепление; в - коробка передач; г - карданная передача; _______- по фактическим данным; - - - - - на основе прогноза
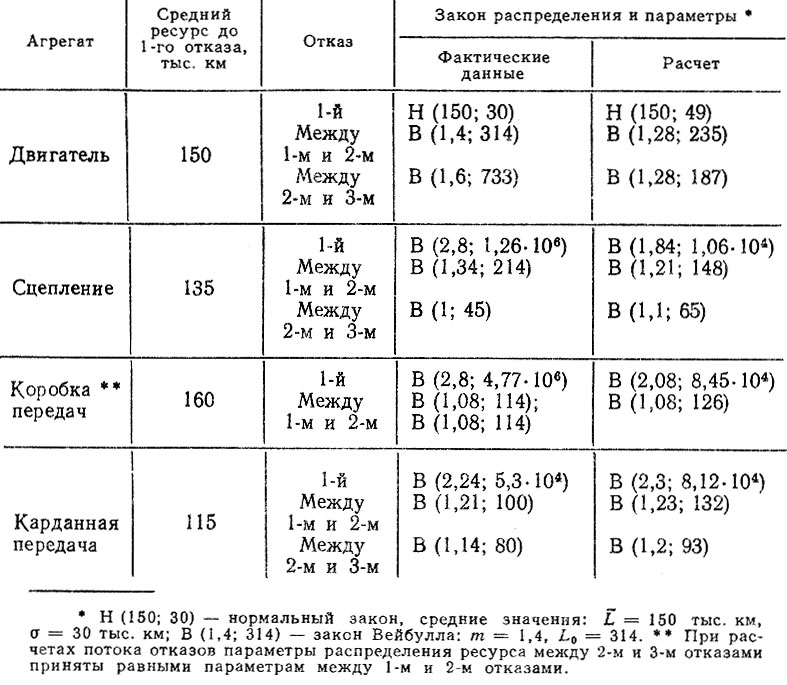
Таблица 3.7.Фактические и расчетные (прогнозные) параметры распределений ресурсов деталей

Таблица 3.8. Оценка расхождения между фактическими и расчетными потоками отказов деталей
Из анализа табл. 8.8 и рис. 8,4 следует: максимальная величина Δω = 15,2%, средняя по четырем деталям - Δω = 9,1%, что можно признать удовлетворительным для прогнозирования потока отказов детали;
чем больше точек пересечения у реализаций потоков, тем меньше коэффициент Δω;
между средней ошибкой определения параметров распределений и коэффициентом Δω однозначной связи не наблюдается, но наименьшим значениям Δω соответствуют и минимальные средние ошибки определения параметров!
параметры распределений до первого отказа должны определяться наиболее точно, так как они суммируются наибольшее количество раз;
при расчете (прогнозе) потоков отказов агрегата с использованием корреляционных зависимостей следует ожидать "стабилизацию" потоков отказов деталей, так как корреляционные зависимости дают средние оценки параметров как больших, так и меньших фактических значений.
Как указывалось выше, для того чтобы расчетный (прогнозный) поток отказов агрегата был адекватен эксплуатационному, необходимо учитывать ряд факторов. Это можно достигнуть введением корректирующих коэффициентов и соответствующих зависимостей.
Корректировка прогнозного потока по числу учитываемых деталей. Поскольку на стадии проектирования в настоящее время отсутствует возможность расчета показателей ресурса всех деталей, то целесообразно включать в расчет только детали, лимитирующие надежность. В общем случае расчетный параметр потока отказов агрегата ωp (L) должен быть домножен на корректирующий коэффициент α (L), зависящий от наработки. При проектировании можно ограничиться средним значением а, величина которого будет также зависеть от принятой методики выбора деталей, лимитирующих надежность; α = 1,05-1,5.
Учет множественности отказов. Из анализа результатов наблюдений за подконтрольными партиями автомобилей следует, что при одном текущем ремонте производится замена от одной до нескольких деталей; среднее число замен (по разным источникам) составляет 1,3-1,6. Учет множественности отказов может быть выполнен двумя способами: с помощью общего корректировочного коэффициента; индивидуальной корректировкой для групп деталей, входящих в сопряжения или сборочные единииы.
При общей корректировке расчет производится по формуле
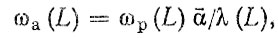 (3.43)
(3.43)
где ωa(L), ωp(L) - откорректированный и расчетный параметры потоков отказов агрегата; λ (L) - коэффициент учета множественности отказов.
Корректировка потока по группам деталей производится с использованием так называемой стратегии замен [76]. Рассмотрим два наиболее часто встречающихся варианта.
Первый вариант сводится к замене всех деталей, входящих в сопряжение или сборочную единицу" в случае отказа одной из деталей. Очевидно, случайная величина наработки сопряжения Z будет определяться минимальной наработкой одной из деталей" т, е. Z = min (х1, x2, ...,xn), где xi - случайная величина на" работки i-и детали до первого отказа. Для нахождения функции и плотности распределения наработки сопряжения необходимо воспользоваться формулами для распределений минимальных значений" приведенными в табл. 2.2, Аналогично поступаем и для определения зависимостей между заменами" т. е. Z1,2 = min (x11,2, x21,2,..,xn1,2) и т. д.
Определим коэффициент λ, приняв" что в сборочную единицу входят n деталей, ресурсы которых до первого и между последующими отказами подчиняются нормальным законам распределения с одинаковыми параметрами L- и σ. На основании асимпотической формулы (3.17) при независимой замене деталей получим параметр потока отказов сборочной единицы
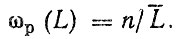
Если все детали заменяются при отказе одной из них, то воспользовавшись формулой (2.39) для среднего значения минимальных величин" подчиняющихся нормальному закону, получим;
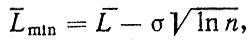
а эксплуатационный параметр потока отказов сборочной единицы
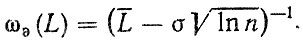
Тогда
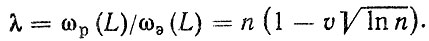 (3.44)
(3.44)
В частном случае при n = 2 и коэффициентах вариации λ = 0,24÷0,33 λ = 1,67÷1,45.
Следует подчеркнуть" что при распределении ресурсов деталей, подчиняющихся экспоненциальным законам с параметрами λ1 и λ2, корректирующий коэффициент λ = 1. Так, по формуле (3.40) ωр = λ1 + λ2, a Lmin = 1 /(λ1 + λ2), т. е. ωэ(L) = ωр(L).
Второй вариант стратегии замен сводится к тому, что замена одной из деталей сопряжения (главной или дорогой [76]) обязательно сопровождается заменой остальных деталей (второстепенных или дешевых); при отказе второстепенных деталей производится их замена. Нетрудно заметить, что при данной стратегии наблюдается случай, рассмотренный в п. 3.2, который сводится к усечению потока отказов второстепенной детали потоком отказов главной детали. Тогда многократное использование формул (3.23) и (3.25) позволяет получать усеченные потоки отказов дешевых деталей, которые затем суммируются о потоком отказов главной детали.
Пример. Допустим, что до первого отказа ресурсы гильз и колец подчиняются нормальным законам с параметрами LΓ, от и LK, σК, приведенными в табл. 3.6, а между отказами распределениям Вейбулла с параметрами: mΓ = 2, L0Γ = 17 778, mK = 1,5, L0K = 838; после замены гильз ресурс колец также подчиняется распределению Вейбулла.
Вначале определим параметр потока отказов гильз
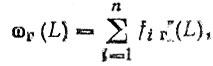 (3.45)
(3.45)где ωГ (L) плотность распределения наработки гильз до i-й замены; n - число замен.
Так,
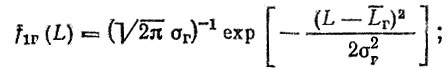 (3.46)
(3.46)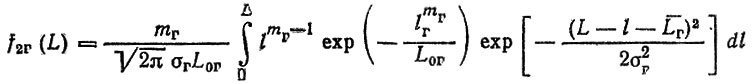 (3.47)
(3.47)и т. д. по рекуррентной формуле для общего процесса восстановления (3.9).
Аналогичные формулы используются и для расчета потока отказов колец на первом этапе.
Усеченный наработками до первого отказа гильз параметр потока отказов колец рассчитывается по формуле (3.24)
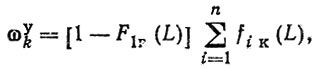
где F1Γ(L) - функция распределения наработок гильз [см, формулу (3.46)].
Воспользовавшись формулой (3.25), определим плотность распределения наработки колец после первой замены гильз
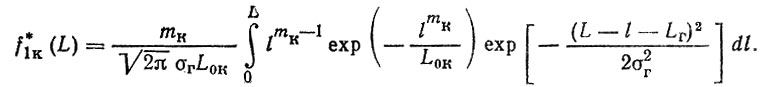
Последующие плотности распределения f*ik (L) находятся с помощью формул композиции. Таким образом, параметр потока отказов колец (после первой замены гильз)
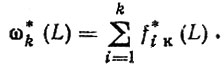
Для усечения потока ω* (L) второй заменой гильз необходимо воспользоваться функцией распределения F2Γ (3.47). Расчет повторяется для определения потока отказов колец после второй замены гильз и т. д.
На рис. 3.5 приведены результаты расчета параметров потоков отказов гильз и колец без учета и с учетом стратегии замен, а также усеченные параметры потоков отказов колец до первой и второй замены гильз. Заштрихованная область на рис. 3.5 позволяет оценить коэффициент множественности отказов X (L) для указанных деталей. Например, на пробеге L < 80 тыс. км λ = 1, при L = 240 тыс. км λ(L) = 1,24 и т. п.
Учет корреляции между параметрами наработок деталей. При расчете потоков отказов с использованием рекуррентных соотношений предполагается, что наработки деталей между отказами являются независимыми случайными величинами. Если параметры наработок, например в виде средних значений и дисперсий, определяются с использованием формул для числовых характеристик случайных величин, то корреляция между наработками учитывается непосредственно. В этом случае расчеты параметров между наработками детали производятся по формулам:
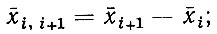 (3.48)
(3.48)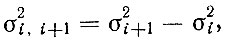 (3.49)
(3.49)где xi+1, xi - средние наработки до (i + 1) и i-го отказов; σi+1, σi - средние квадратические отклонения до (i + 1) и i-го отказов.
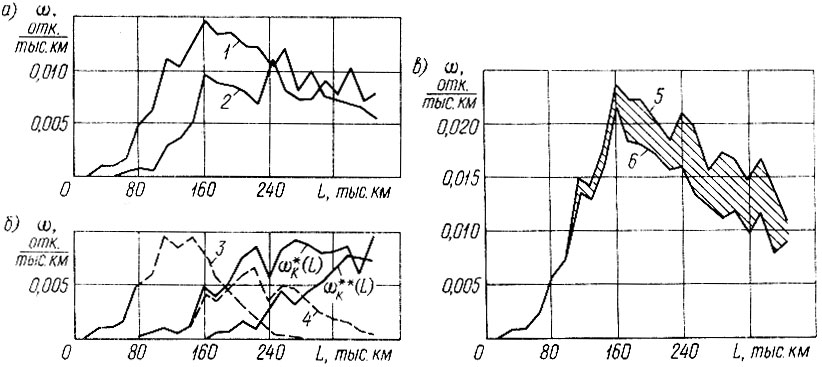
Рис. 3.5. Определение коэффициента множественности отказов двигателя: а - исходные потоки отказов колец (1) и гильз (2) без учета стратегии замен; б - потоки отказов колец ω*K(L) и ω**Γ(L), 'усеченные' первой (3) и второй (4) заменой гильз; в - суммарные потоки отказов колец и гильз без учета (5) и с учетом (6) стратегии замен
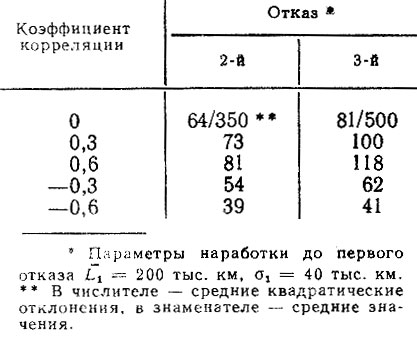
Таблица 3.9. Параметры распределений для расчета потока отказов с учетом коррекции, тыс. км
Если параметры наработок между отказами детали определяются для каждого агрегата в виде разности случайных величин xj,i+1 - xj,i где j - номер агрегата, то формула (3.49) записывается в виде
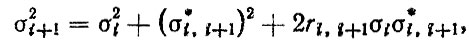 (3.50)
(3.50)где σ*i,i+1 - средние квадратические отклонения между (i + 1) и t-м отказами, определяемые с учетом наработок для каждого агрегата; r - коэффициент корреляции, -1 < r < 1.
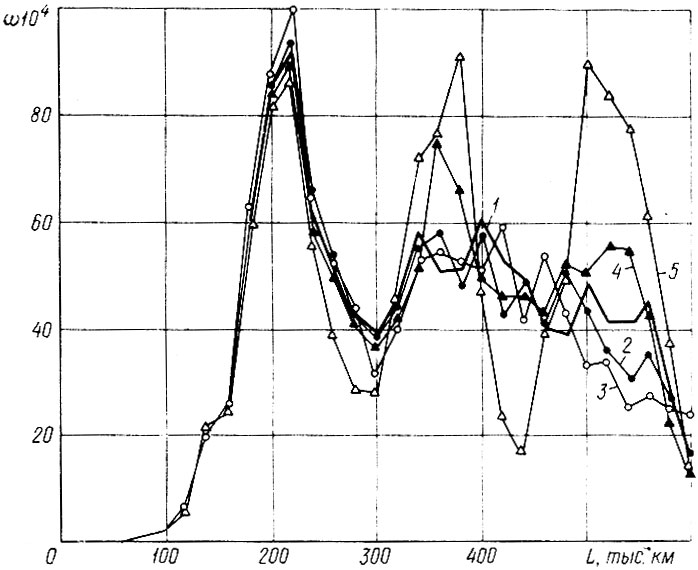
Рис. 3.6. Потоки отказов детали a (L), определенные с учетом корреляции r между наработками: 1 - r = 0; 2 - 0,3; 3 - 0,6; 4 - 0,3; 5 -0,8
На рис. 3.6 приведены результаты расчетов ω(L) при различных r с учетом корреляции между наработками по формуле (3.50) Исходные данные для расчета приведены в табл. 3.9. При расчетах предполагалось" что наработки до первого, второго и третьего отказов подчиняются нормальному закону.
Из анализа ω (L) следует, что при r > 0 влияние корреляции между наработками можно не учитывать. При r < -0,3 при расчете потока отказов с использованием плотностей распределения f (xi+1, σi+1) без учета корректировки σi+1 по формуле (3.50) будут наблюдаться значительные отклонения между фактическими и расчетными потоками отказов по интервалам пробега. В этом случае для повышения точности необходимо определять двумерные распределения φ(xi, xi,i+1), а расчет f (xi+1) должен производиться по формуле
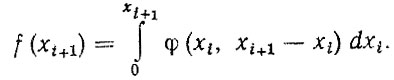 (3.51)
(3.51)Учитывая трудности расчетного определения коэффициентов ri,i+1 и φ(xi, xi+1) на этапе проектирования, следует дополнить существующую методику статистической обработки данных об эксплуатационной надежности соответствующими методами, позволяющими оценивать ri,i+1 и φ(xi, xi+1).
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'