3.2. Расчет потоков отказов деталей автомобиля

Анализу и расчету потоков отказов, представляющих сумму независимых неотрицательных случайных величин, посвящен один из разделов теории вероятностей - теория восстановления [14, 31]. Из большого количества различных процессов наибольший интерес представляют следующие: простой, при котором все функции распределения наработок до первого F₁(L) и между последующими отказами F_{i, i+1}(L) равны; общий, при котором ограничения на равенство функций распределения не распространяются на первую из них, т. е. F₁(L), F_i,i+1(L) = F (L); сложный [46], при котором F₁(L) и F_i,i+1(L) различны.

Основной характеристикой процесса восстановления является функция восстановления

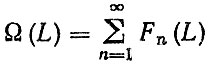(3.4)

и ее дифференциальная характеристика - плотность восстановления

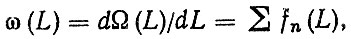(3.5)

где F_n (L), f_n (L) - функция и плотность распределения наработки деталей до n-го отказа.

Согласно ГОСТ 27.002-83, функция восстановления Ω (L) получила название ведущей функции потока отказов, а плотность восстановления ω(L) - параметра потока отказов. Эти термины будем использовать в дальнейшем.

В общем виде Ω (L) и и ω(L) определяются с помощью рекуррентных зависимостей, вывод которых рассмотрим на примере простого процесса восстановления. Известно, что сумма независимых случайных величин X и Y с законами распределения f₁(x) и f₂ (у) является случайной величиной Z, подчиняющейся закону распределения f (z). Такая операция называется композицией законов распределения. Если случайные величины X и Y являются положительными, то расчетная формула записывается в виде свертки

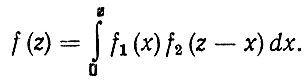(3.6)

Воспользовавшись операционным исчислением, запишем формулу (3.6) в виде

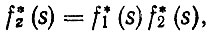(3.7)

где f^*_z(s), f₁^*(s), f^*₂(s) - соответственно изображения функций f (z), f₁ (x), f₂ (y).

Многократное использование формулы (3.7) позволяет получить плотности распределения для соответствующей суммы случайных величин.

Для простого процесса восстановления все f^* (s) равны. Тогда, для n-го члена суммы имеем (3.7) f_n (s) = [f^* (s)]. Эту зависимость можно представить как n-й член геометрической прогрессии со знаменателем f^* (s). Поскольку f^* (s) < 1, то для предельного значения суммы членов геометрической прогрессии получим

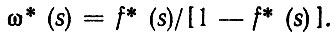
Осуществив обратный переход от изображений к оригиналам, найдем

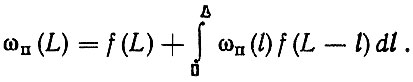(3.8)

Аналогично для общего процесса восстановления

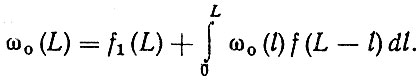(3.9)

Для расчета Ω (L) и ω (L) используются, как правило, численные методы, в частности метод статистических испытаний, Для некоторых законов распределения n-кратная свертка вычисляется в конечном виде.

Нормальный закон. Если наработки до первого отказа детали

и между отказами подчиняются нормальным законам с параметрами L_i σ_i то плотность распределения до n-го отказа

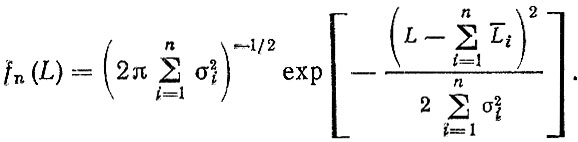(3.10)

Вывод формулы (3.10) основан на том, что сумма нормально распределенных случайных величин также подчиняется нормальному закону. Тогда параметр потока отказов для сложного процесса восстановления будет иметь вид

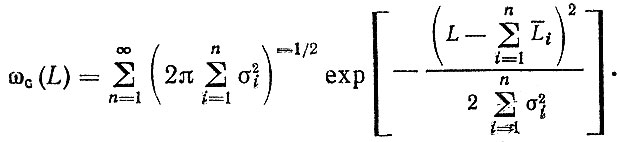(3.11)

Из формулы (3.11) могут быть получены частные случаи для простого и общего процессов восстановления.

Экспоненциальный закон. Если наработки детали до первого и между последующими отказами подчиняются экспоненциальным законам с параметрами то плотность распределения до n-то отказа является обобщенным законом Эрланга n-го порядка [16]

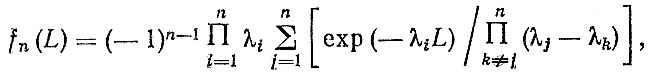(3.12)

где

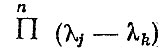
произведение всех биномов при k = 1, 2,....,(j - 1), (j + 1), ..., n.

Для сложного процесса восстановления параметр потока отказов

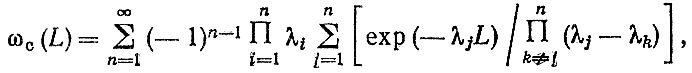(3.13)

а ведущая функция потока отказов

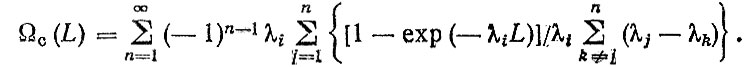(3.14)

Соответственно для простого процесса восстановления плотность распределения до n-го отказа подчиняется закону Эрланга n-го порядка

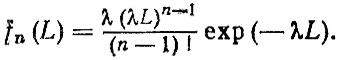(3.15)

а ведущая функция потока отказов записывается в виде

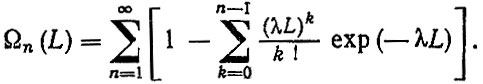(3.16)

При анализе потоков отказов деталей могут быть использованы асимптотические формулы. В случае общего процесса восстановления эти формулы следующие:

для ведущей функции потока отказов

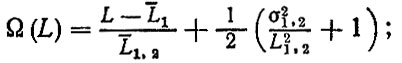(3.17)

параметра потока отказов

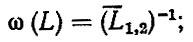(3.18)

дисперсии числа отказов (восстановлений)

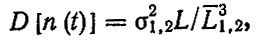(3.19)

где L₁ среднее значение ресурса до первого отказа; L_1,2, σ_1,2 - среднее значение и среднее квадратическое отклонение ресурса между отказами.

Считается, что асимптотические формулы дают точные оценки Ω (L), ω (L), D (L) при наработке, превышающей величину переходного периода L_n. Под переходным периодом понимается на-работка, при которой дисперсия случайной величины числа отказов D (L) ∼ 1, Для общего процесса восстановления L_n определяется по формуле

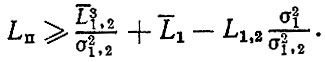(3.20)

При условии σ₁ = σ_1,2, L₁ = L_1,2 по формулам (3.17)-(3,20) рассчитываются асимптотические оценки для простого процесса восстановления.

Формулы для простого, общего и сложного процессов восстановления используются в расчетах потоков отказов элементов таких систем, которые не подвергаются ремонтам в процессе эксплуатации. Но основная особенность формирования потоков отказов механических восстанавливаемых систем, в частности агрегатов автомобилей, состоит в том, что помимо отказов, определяемых предельным состоянием элементов и устраняемых текущим ремонтом, происходит искусственное усечение потока вследствие капитальных ремонтов агрегата, капитальных ремонтов автомобиля, а также списания агрегата и автомобиля. Таким образом, в общей методике расчета потока отказов деталей должны быть учтены три момента: усечение потока отказов капитальными ремонтами агрегатов (автомобиля) и списанием; формирование потоков после капитальных ремонтов; определение показателей ресурса деталей, поступающих в капитальный ремонт.

Выведем формулу для потока отказов детали с учетом капитального ремонта агрегата. Рассмотрим два соотношения для случайных величин наработок детали L_i до i-го отказа и агрегата до капитального ремонта R. Если L_i > R, то деталь заменяется при текущем ремонте и i-и отказ детали учитывается в потоке отказов. В случае L* > R /-й отказ детали не учитывается, у детали имеется остаточный ресурс L₀ = L_i - R > 0.

Допустим, что случайные величины L_i и R независимые и подчиняются плотностям распределения f_i (L) и f_R (L). Тогда на отрезке времени 0, L вероятность отказа детали будет определяться произведением вероятности наступления отказа детали на условную вероятность того, что на отрезке не производился капитальный ремонт агрегата" Тогда, по формуле полной вероятности можем записать

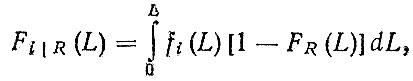(3.21)

где F_R (L) - функция распределения наработок агрегата до капитального ремонта.

При L → ∞ получим долю отказов деталей, наступивших до капитального ремонта,

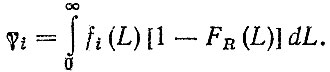(3.22)

Необходимо отметить сходство формул (1.17) и (3.22). Поскольку вывод формулы (3.22) отличается от рассмотренного в работе [28] для получения вероятностных оценок при расчетах на статическую прочность, это позволяет получить усеченную плотность распределения наработок до i-го отказа в виде

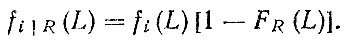(3.23)

При подстановке F_R (L) в формулу (3.5) получим выражение для потока отказов детали, усеченного капитальным ремонтом агрегата,

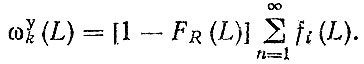(3.24)

При подстановке вместо F_R (L) соответствующих функций распределения формула (3.24) может быть применена для расчета усеченного потока отказов детали с учетом капитального ремонта автомобиля, а также списания агрегата или автомобиля.

Для определения параметра потока отказов детали после капитального ремонта агрегата допустим, что случайные величины R и Θ (Θ - наработка детали до первого отказа после капитального ремонта) независимы и подчиняются плотностям распределения f_R (L) и f_Θ (L). Воспользовавшись формулой композиции случайных величин" получим плотность распределения наработки детали до первого отказа с учетом капитального ремонта

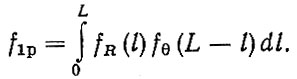(3.25)

Аналогично определяются и плотности распределения до последующих отказов" Таким образом, параметр потока отказов детали капитально отремонтированного агрегата

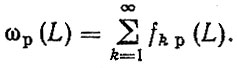(3.26)

Принципиальное отличие потоков отказов деталей нового и капитально отремонтированного агрегата заключается в том, что первый из них имеет фиксированную точку отсчета L = 0, а начало второго определяется случайной величиной R.

Очевидно, ω_p (L) также будет усечена функцией распределения наработки агрегата до второго ремонта или до капитального ремонта автомобиля и т. д. Таким образом, суммируя параметры потоков отказов для соответствующих межремонтных циклов, находим параметр потока отказов детали на пробеге от начала эксплуатации до списания автомобиля

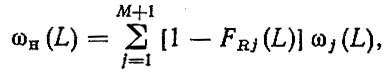(3.27)

где М - число капитальных ремонтов агрегата; F_Rj (L) - функция распределения наработки до j-го капитального ремонта агрегата или списания автомобиля; ω_j (L) - параметр потока отказов для соответствующего межремонтного цикла,

Следует подчеркнуть, что речь идет об отказах деталей, заменяемых при текущих ремонтах. Если же требуется учесть и замены деталей при капитальном ремонте агрегата, то в формулу (3.27) необходимо ввести еще одну составляющую, отражающую число этих замен. Наиболее просто это можно сделать с помощью коэффициента сменности при капитальных ремонтах. Тогда, общий параметр потока отказов запишется в виде

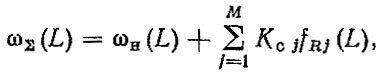(3.28)

где К_{c j} - коэффициент сменности детали при j-м капитальном ремонте агрегата.

Для деталей, которые подлежат 100% замене при капитальных ремонтах, К_{с j} = 1- Если детали не выбраковываются, то К_{с j} = 0.

Рассмотрим вопрос об остаточном ресурсе детали L₀ агрегата, поступившего в первый капитальный ремонт. Вначале запишем формулу для плотности распределения наработок агрегата f_zi (L), превышающих наработку до i-го отказа детали,

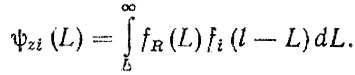
Тогда, плотность распределения остаточного ресурса детали определяется по формуле

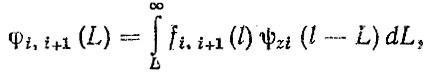(3.30)

где φ_{i, i+1} (L), f_{i, i+1} (l) - соответственно плотности распределения остаточного ресурса и наработок детали между i-м и (i + 1)-м отказами.

Наконец, плотность распределения остаточного ресурса всех деталей агрегата, поступившего в первый капитальный ремонт запишется в виде

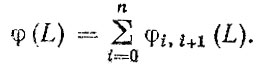(3.31)

С помощью формул (3.29)-(3.31) производится расчет остаточных ресурсов детали и для последующих межремонтных циклов, Следует иметь в виду, что при определении остаточного ресурса наработок до первого отказа, расчет производится сразу по формуле (3.30), при этом под f_0,1 (L) понимается плотность распределения наработок до первого отказа f₁(L), а вместо ψ_zi(L) подставляется плотность распределения наработок агрегата до капитального ремонта f_R (L). Для последующих отказов сначала рассчитывается ψ_zi(L), а затем φ_{i, i+1}(L).

При наличии плотности распределения остаточного ресурса детали φ (L) представляет интерес определение зависимости между остаточным ресурсом L₀ и наработкой до первого отказа после капитального ремонта Θ [см. (3.25)]. Для этого разделим детали на три группы: первую, в которую входят детали с К_c = 1; вторую, включающую перемонтируемые детали (0 < К_с < 1)" при этом часть деталей выбраковывается, а остальные устанавливаются без восстановления на отремонтированном агрегате; третью, включающую восстанавливаемые детали.

Для первой группы деталей остаточный ресурс не имеет связи с наработкой до первого отказа после капитального ремонта и подчиняется плотности распределения f_Θ (L), Для второй группы деталей плотность распределения f_Θ (L) можно представить в виде суперпозиции (линейной комбинации)

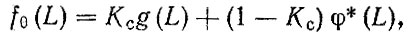(3.32)

где φ^* (L) - плотность распределения остаточного ресурса детали с учетом выбраковки при капитальном ремонте; g (L) - плотность распределения наработки детали, установленной при капитальном ремонте вместо выбракованной.

Следует заметить, что при К_с = 0, т. е. когда детали устанавливаются без замены и восстановления, f_Θ(L) = φ (L), где φ (L) определяется по формуле (3.31); для деталей такого типа капитальный ремонт агрегата не вносит изменения в параметр и ведущую функцию потока отказов.

Для третьей группы также воспользуемся формулой супер-позиции

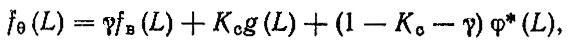(3.33)

где γ - доля деталей, подвергающихся восстановлению; f_в (L) - плотность распределения наработки до отказа восстановленной детали.

Если f_в (L) = g (L), т. е. плотности распределения наработок восстановленных и замененных при капитальном ремонте деталей совпадают, то

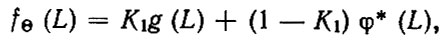(3.34)

где K₁ = γ + K_c.

Наиболее сложным является вопрос определения К_с, γ и остаточного ресурса детали с учетом выбраковки при капитальном ремонте φ^* (L). Рассмотрим возможный вариант расчета, основанный на логической модели ресурса детали.

1. Выявляются реализации процессов ζ_i(L) в i-x сечениях детали, приводящих к отказу. Для случайных моментов наработок до капитального ремонта R определяются значения реализаций процессов ζ_i(L = R), т. е. двумерная плотность распределения φ_i (ζ, R), с помощью которой находится одномерная плотность по формуле

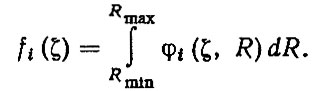(3.35)

2. Ha основании допустимых (предельных) значений с_{п i} рассчитываются вероятности выбраковки деталей для каждого i-го сечения

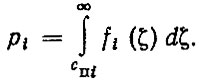(3.36)

3. Для определения коэффициентов К_с и γ воспользуемся общей теоремой о повторении опытов, согласно которой

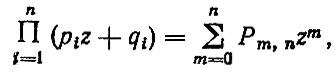(3.37)

где qi - вероятность годности детали в i-м сечении; n - число рассматриваемых сечений детали; Р_m,n - вероятность появления события A равно m раз в результате n опытов.

Вероятность Р_m,n определяется как коэффициент при одинаковых степенях z^m после раскрытия скобок в левой части тождества (3.37). Поскольку для каждого предельного значения с_{п i} предполагается известным (производится выбраковка или восстановление детали), то суммируя члены с соответствующими р_i, находим коэффициенты K_c и γ.

4. На последнем этапе для деталей, признанных годными, оценивается плотность распределения остаточного ресурса φ(L). Особенность расчета здесь заключается в том, что начальные значения реализаций ζ_i (R) описываются двумерным распределением φ_i(ζ, R). При этом случайные величины ζ_i(R) являются засеченными, так как ζ_i (R) ≤ c_{п i}. Наиболее целесообразный путь решения - использование методов статистического моделирования.

В первом приближении возможен упрощенный вариант, при котором полагаем, что наработка детали, имеющей остаточный ресурс L₀ (или φ (L)), не меньше некоторой гарантированной величины L_г. Тогда, остаточный ресурс будет определяться усеченной плотностью распределения φ^* (L) = φ (L/L_г) при L ≥ L_г, а коэффициент

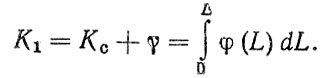(3.38)

Таким образом, методика позволяет производить расчеты потоков отказов деталей с учетом особенностей механических восстанавливаемых систем.