Глава 3. Методы расчета единичных и комплексных показателей надежности агрегатов автомобиля

3.1. Определение зависимостей между параметрами ресурсов деталей

Для расчета потоков отказов агрегатов автомобиля необходимо знать законы распределения ресурсов деталей до первого и после-дующих отказов, На стадии проектирования эти законы определяются расчетным путем с использованием логических моделей ресурса деталей. Однако разработанным моделям (см. гл. 2) присущи и определенные недостатки, главными из которых являются их гипотетический характер, упрощение сложных взаимосвязей между деталями, отсутствие учета изменения от времени (пробега) состояния агрегатов, т. е. нагрузочных режимов и предельных состояний. Возможен иной подход к расчету, когда прогноз (расчет) параметров ресурса детали выполняется только до первого отказа (замены), а ресурсы до последующих отказов (второго, третьего и др.) определяются с помощью корреляционных зависимостей, устанавливаемых по результатам статистической обработки данных об эксплуатирующихся моделях автомобилей. Такой подход, на наш взгляд, правомерен по двум причинам" во-первых, при расчете ресурса детали до первого отказа в ряде случаев можно не учитывать изменение характеристик нагрузочного режима и предельных состояний, т. е. упрощение является оправданным; во-вторых, корреляционные зависимости объективно отражают взаимосвязь между причинами отказов деталей и параметрами распределений их ресурсов, что существенно упрощает всю процедуру расчета.

Анализу зависимостей между параметрами ресурсов деталей, а также рассеиванию ресурсов как до первого отказа, так и между отказами посвящен ряд исследований [34, 36, 46]. В качестве характеристик рассеивания ресурсов используются дисперсии (средние квадратические отклонения), коэффициенты вариации υ, параметры сдвига. На рис. 3.1 приведены зависимости между средними значениями L₁ и средними квадратическими отклонениями σ₁ ресурсов деталей автомобиля до первого отказа. Из рис. 3.1. видно, что между указанными параметрами наблюдается тесная связь; корреляционное уравнение записывается в виде (L₁, σ₁ - в тыс. км)

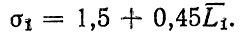(3.1.)

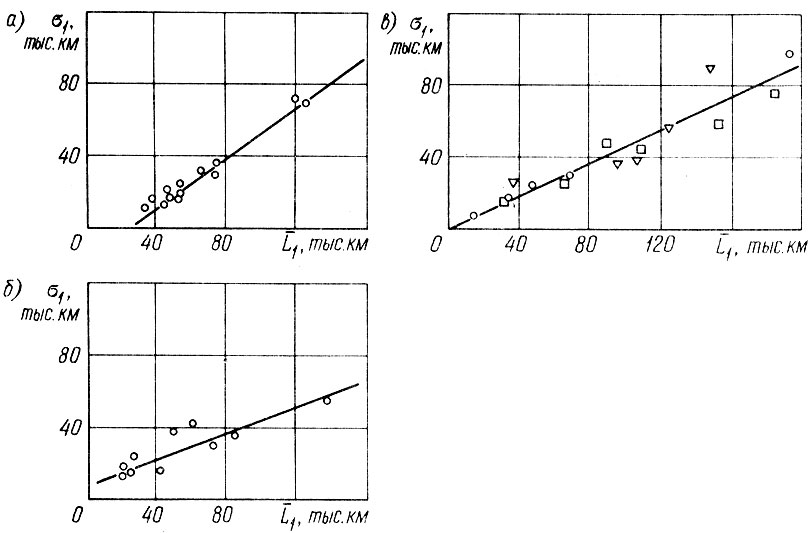
Рис. 3.1. Зависимость между средними квадратическими и средними значениями ресурсов деталей до первого отказа: а - накладки сцепления; б - карданные шарниры; в - рессоры (Ο - передние, □ - задние, ∇ - дополнительные)

О наличии корреляционной связи между коэффициентами вариации и и средними значениями ресурсов L свидетельствует зависимость, приведенная на рис. 3.2. Большой разброс объясняется, в частности, тем, что в выборку включены детали, причины отказов которых связаны с различными разрушительными процессами. В этой связи представляют интерес данные работы [34], согласно которым коэффициенты вариации ресурсов при различных видах разрушения следующие: износ (детали сдвига υ = 0,3; контактная усталость - υ = 0,5 (подшипники качения υ = 0,7÷0,9).

Практически во всех исследованиях отмечается уменьшение средних ресурсов с увеличением номера замены деталей" Так, по данным работы [1], пробеги до 2-, 3", 4-й замены вкладышей подшипников коленчатого вала (без перешлифовки) в процентах от пробега до первой замены составили:

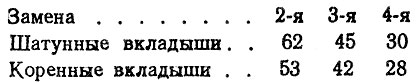
Для деталей тракторов наблюдается аналогичная картина (табл. 3.1.). По данным стендовых испытаний [18] скорость изнашивания нижних коренных вкладышей увеличилась в 1,36 раза, верхних шатунных вкладышей - в 1,15 раза. У капитально отремонтированных двигателей скорости изнашивания вкладышей коренных подшипников возросли в 1,5 раза, верхних поршневых колец (по высоте) - в 1,7 раза, гильз цилиндров - в 1,9 раза [39].

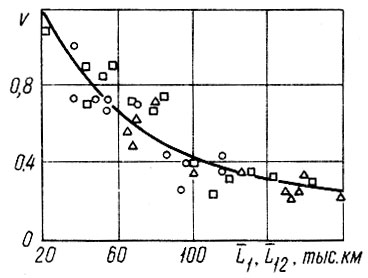
Рис. 3.2. Зависимость между коэффициентами и средними значениями ресурсов деталей двигателей

Таблица 3.1. Параметры ресурсов деталей трактора между заменами, моточасы [46]

Уменьшение средних наработок после замены можно обосновать с помощью моделей ресурса деталей. Например, при описании зазора как

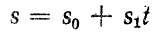
среднее и среднее квадратическое отклонения ресурса, определяемые достижением предельного зазора s = с_п, находятся по формулам (метод линеаризации):

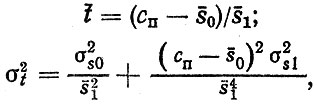
(3.2)

где s₀, s₁ - средние значения начального зазора и скорости изнашивания; σ_s0, σ_s1 - средние квадратические отклонения"

Пример. Рассмотрим сопряжение ""верхнее кольцо-канавка в поршне", Примем (поданным работ [16, 18, 48]) для нового двигателя s₀ = 80 мкм, σ_s0 - = 20 мкм; s₁ = 2,2 мкм/тыс. км; σ_s1 = 0,6 мкм/тыс. км; c_п = 360 мкм; после замены поршневых колец - s₀ = 120 мкм; σ_s0 = 30 мкм; s₁ = 2,5 мкм; σ_s1 = 0,72 мкм. Тогда по формулам (3.2) находим средний ресурс колец до первой замены t₁ = 136 тыс, км (σ_t1 = 38 тыс. км), а между заменами t_p = 96 тыс. км (σ_p = 30 тыс. км). Уменьшение среднего ресурса колец Δt = 40 тыс. км определяется на 1/3 увеличением скорости изнашивания и на 2/3 увеличением начального зазора в сопряжении "верхнее кольцо - канавка поршням.

Для определения корреляционных зависимостей между пара-метрами ресурса были составлены выборки, главным образом, по деталям, лимитирующим надежность (табл. 3.2). Данные о ресурсах деталей автомобилей ЗИЛ, ГАЗ, МАЗ, автобусов ЛАЗ получены в результате наблюдений, проведенных в автотранспортных предприятиях Ленинграда, а также взяты из работ [25, 36, 52]. Подконтрольные партии автомобилей эксплуатировались в основном в условиях больших городов (III категория условий эксплуатации согласно [53]). Следует отметить, что средние ресурсы (наработки) и характеристики рассеивания для одинаковых деталей одних и тех же моделей автомобилей могут существенно различаться, в частности, из-за того, что практически не фиксируется состояние деталей при замене. Поскольку лишь для небольшой номенклатуры деталей удается получить полные выборки наработок до замены, то для большинства деталей выборки являются незавершенными (многократно усеченными) и это вносит дополнительные погрешности в оценки параметров. При расчетах в качестве аргумента принимались средние ресурсы деталей до первого отказа L₁ или средние ресурсы деталей между первым и вторым отказами L_1,2 и вторым и третьим отказами L_2,3. В качестве функции принимались L_1,2, L_2,3, средние квадратические отклонения ресурсов до первого отказа σ₁, между первым и вторым отказами σ_1,3 и вторым и третьим отказами σ_2,3 а также коэффициент вариации ресурсов до первого отказа υ₁. Расчеты проводились как для линейной, так и для гиперболической, экспоненциальной, степенной и логарифмической зависимостей; коэффициенты корреляционных зависимостей определялись с использованием метода наименьших квадратов. Результаты расчетов - коэффициенты а₀ и а₁ линейной зависимости y = а₀ + а₁L и пределы изменения аргумента L, внутри которых подбирались корреляционные зависимости - приведены в табл. 3.3-3,5. На рис. 3,3 для примера приведены некоторые зависимости для деталей карданной передачи.

Таблица 3.2. Агрегаты и детали, дли которых определялись зависимости между параметрами ресурса

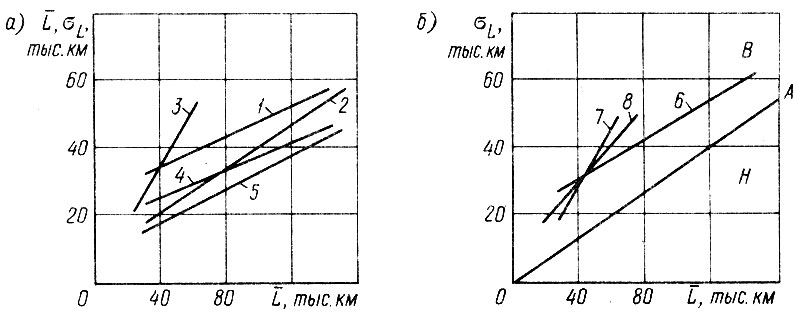
Рис. 3.3. Корреляционные зависимости между параметрами ресурсов карданной передачи:

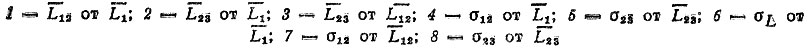
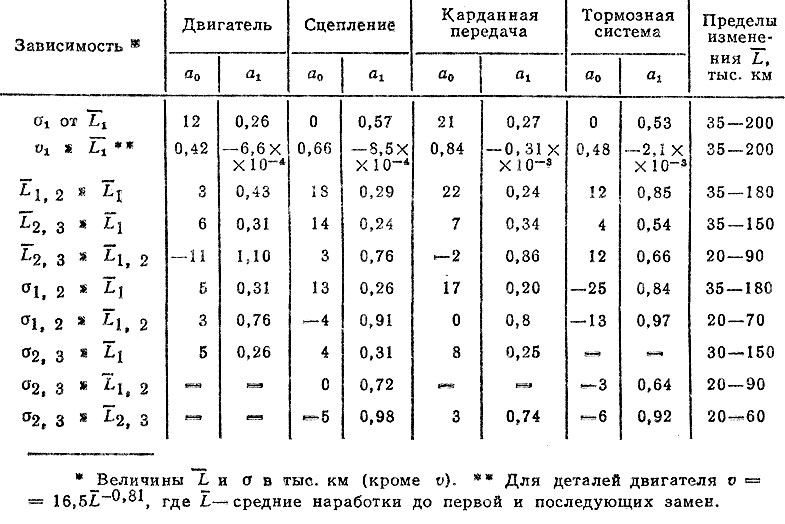
Таблица 3.3. Коэффициенты корреляционной зависимости между параметрами ресурсов деталей агрегатов

Анализ результатов расчета позволяет сделать следующие выводы.

1. Для всех деталей агрегатов автомобиля наблюдается тенденция уменьшения средних ресурсов между последующими отказами по сравнению со средним ресурсом до первого отказа. Это обусловлено, в первую очередь, спецификой проведения текущих ремонтов в условиях АТП; качеством деталей ремонтного фонда (запасные части, восстановленные детали); нарушением сопряжений деталей, в частности увеличением зазоров, и т. п.

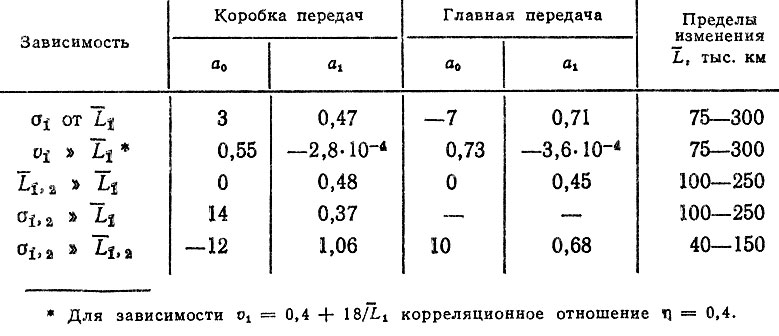
Таблица 3.4. Коэффициенты корреляционных зависимостей между параметрами ресурсов деталей агрегатов

Таблица 3.5. Коэффициенты корреляционной зависимости σ₁ = а₀ + a₁L₁ для деталей одного наименования

2. Поскольку в 50% случаев по величине корреляционного отношения η предпочтительной является линейная зависимость, а в 80% различие между линейной и другими зависимостями было незначительным (не более 5% по величине η), то для прогнозных расчетов можно использовать линейную зависимость. Повышение точности расчета по корреляционным зависимостям может быть достигнуто при включении в выборки деталей только одного наименования (см. табл. 3.5).

3. Наблюдается тесная корреляционная связь между рассматриваемыми параметрами средних значений и средних квадратических отклонений! в некоторых вариантах величина корреляционного отношения η близка к единице и, следовательно, зависимость приближается к функциональной. Для зависимостей υ₁ от L₁ величины корреляционных отношений невелики (η = 0,2÷0,4). Это объясняется тем, что между σ₁ и L₁ наблюдается сильная корреляция, соответственно для υ₁ = f(L₁), где υ₁ = σ₁/L₁ картина обратная.

В целях оценки величин ошибок параметров наработок деталей были выполнены расчеты для автомобилей КамАЭ-5320, эксплуатировавшихся в АТП Ленинграда. В табл. 3.6 приведены результаты расчетов, при этом величины σ₁, L_1,2, σ_1,2 определялись в функции от L₁ по формулам, приведенным в табл. 3.3-3.5.

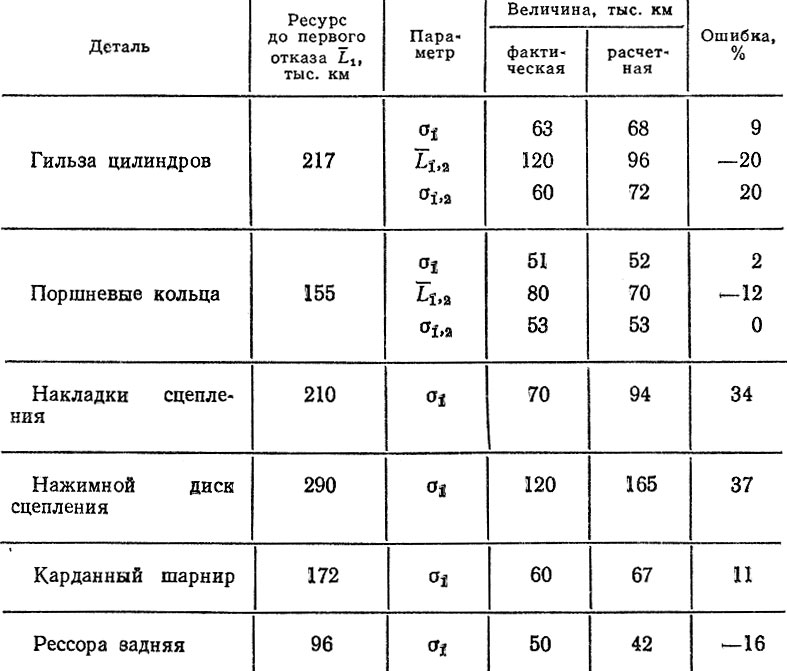
Таблица 3.6. Расчетные (прогноз) и фактические значения параметров ресурсов деталей

Например, для гильзы цилиндра находим (при L₁ = 217 тыс, км) σ₁ = 12 + 0,26L₁ = 68 тыс. км; L_1,2 = 3 + 0,43L₁ = 96 тыс. км; σ_1,2 = 5 + 0,31L₁ = 72 тыс. км.

Ошибка расчета определялась по формуле, %,

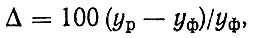(3.3)

где y_р, y_ф - соответственно расчетные и фактические значения параметров.

Обобщение результатов расчета параметров распределений для деталей двигателя, трансмиссии, подвески показало: абсолютные средние ошибки прогноза составили |Δσ₁| = 9,0%, |ΔL_1,2| = 12,3%, |Δσ_1,2| = 11,0%; средние ошибки - Δσ₁ = -5,1 %, ΔL_1,2 = -12,3%, Δσ_1,2 = 3,0%.

По мере накопления статистической информации о новых моделях автомобилей корреляционные зависимости должны корректироваться. В частности, зависимость L_1,2 = f(L₁). Для деталей двигателя, которая дает заниженные оценки, после корректировки записывается в виде L_1,2 = 12 + 0,43L₁; для сцепления ₁ = 0,35L₁.