2.6. Синтез прогнозов показателей ресурса деталей

Специфика прогнозов ресурсов деталей объясняется их при-родной неопределенностью, т. е. отсутствием в настоящее время полного физического и математического описания причин отказов. Например, несмотря на то, что в среднем при использовании корректированного варианта гипотезы суммирования повреждений (при программном нагружении) рассчитанные ресурсы совпадают с фактическими, однако в каждом конкретном случае нет уверенности, что полученный расчетом ресурс будет близок к фактическому. Аналогичная ситуация возникает и при использовании КУД, включающих временной тренд или какой-либо другой метод.

Таким образом, несовершенство методик расчета (прогнозирования) ресурсов деталей приводит к получению нескольких вариантов и задача состоит в отыскании оптимального решения.

В теории прогнозирования общепризнанной классификации методов и стратегий составления прогноза нет. В то же время каждый метод обладает определенной достоверностью, имеет свои преимущества и недостатки. В этой связи наиболее перспективными следует считать комбинированные методы прогнозирования (синтез прогнозов), которые позволяют компенсировать недостатки одних способов достоинствами других.

Синтез прогнозов ресурса следует рассматривать как принятие решения в условиях неопределенности с вероятностной оценкой непротиворечивости результатов. Накопленный опыт составления комбинированных прогнозов позволил сформулировать основные этапы усовершенствованной методики, блок-схема которой приведена на рис. 2.12, В блоках 1 и 2 определяются параметры и плотности распределения вариантов прогноза ресурсов детали f_j (L), при этом j = 1,...,N, N ≥ 2.

Если хотя бы один из вариантов позволяет оценить граничные значения прогноза ресурса, то это необходимо выполнить (блок 3). Установление границ, например, в виде средних значений позволяет гарантировать, что комбинированный прогноз и фактический ресурс находятся внутри "вилки" граничных значений. Помимо этого из рассмотрения следует исключить те варианты прогноза, оценки которых находятся вне граничных значений.

В работах [57, 73] при комбинированном прогнозе рассматривают два варианта: один, полученный методом экстраполяции, другой - экспертным методом. Непротиворечивыми считаются прогнозы, если выполнено неравенство |t| ≤ t_табл(p, υ), где |t| - модуль расчетного значения критерия Стьюдента; t_табл (р, υ) - табличное значение критерия Стьюдента для р-го уровня надежности и числа степеней свободы υ = N₁ + N₂ - m - 1 (N₁ - число наблюдений динамического ряда, m - число пара" метров экстраполяционной зависимости, N₂ - число экспертов).

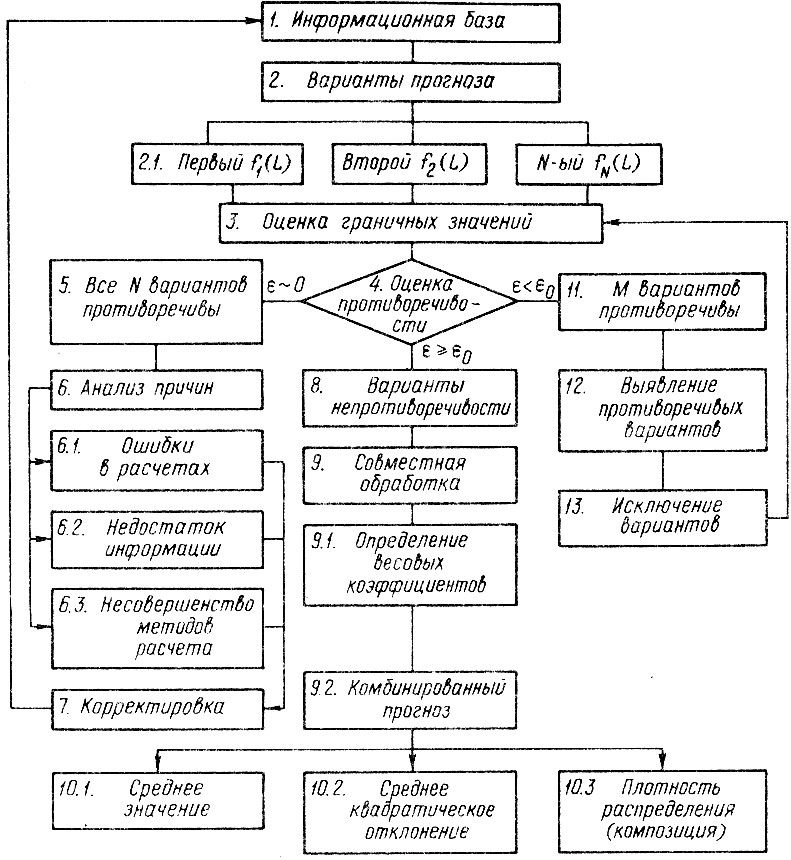
Рис. 2.12. Схема составления комбинированного прогноза ресурса деталей

При такой оценке непротиворечивости речь фактически идет об использовании параметрических методов определения принадлежности выборок к одной генеральной совокупности. Однако эти методы не могут быть использованы, если хоть один из вариантов прогноза получен аналитически (т. е. без использования выборки объемом N_j). Следует заметить, что возможно дальнейшее развитие применения параметрических и непараметрических методов оценки однородности, основанное на моделировании N_j значений выборки.

Рассмотрим другой подход к раскрытию понятия "непротиворечивость". Введем весовую функцию (или функцию принадлежности) δ(L), представляющую собой общую площадь под кривыми плотностей распределения ресурсов f_j (L). Тогда вероятностную меру непротиворечивости можно оценить по формуле

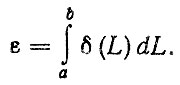(2.74)

Если воспользоваться соотношением ε > ε₀ можно, получить решающее правило для определения непротиворечивости, где ε₀ - заданная доверительная вероятность.

Оценим возможные случаи взаимного расположения плотностей распределения f_j (L). В первом случае (рис, 2.13) области значений f_j (L) не совпадают (ε = 0) и, следовательно, все N вариантов противоречивы (блок 5). После анализа причин (блок 6) необходимо выполнить корректировку методов прогноза ресурса (блок 7), воспользовавшись обратной связью. К первому случаю следует отнести и такой вариант взаимного расположения f_j (L), когда ε ≤ ε_н, где ε_H = 0,05 ÷ 0,10.

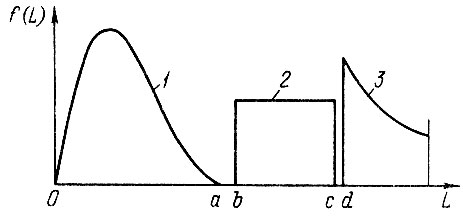
Рис. 2.13. Противоречивый трехвариантный прогноз, ε = 0: 1 усеченное распределение f₁(L), 0 ≤ L ≤ а; 2 - равновероятное распределение f₂(L), b ≤ L ≤ с; 3 - экспоненциальное распределение f₃(L) с параметром сдвига L_c = d

Во втором случае, соответствующем неравенству ε_н < ε < ε₀, полагаем, что некоторые варианты прогноза противоречивы (блок 11). Путем целенаправленного перебора (блок 12) с последовательным исключением тех вариантов, которые приводят к максимальному приросту в (блок 13), добиваемся выполнения соотношения ε > ε₀. Для примера на рис. 2.14, а приведен пяти вариантный прогноз ресурса карданного шарнира с ε = 0,3. При исключении вариантов 2 и 4 удалось повысить степень непротиворечивости до ε = 0,575 (рис. 2.14, б).

Наконец, в случае ε > ε₀ считаем, что варианты непротиворечивы (блок 8) и могут быть совместно обработаны.

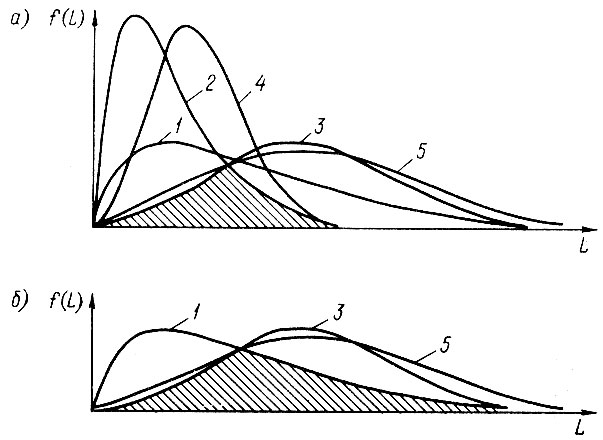
Рис. 2.14. Повышение меры непротиворечивости прогноза путем исключения вариантов: а - пятивариантный прогноз, ε = 0,3; б - трехвариантный прогноз, ε = 0,575; 1 - 5 - варианты прогноза плотностей распределения ресурса детали

Совместная обработка (блок 9) включает выбор правила составления комбинированного прогноза и определение его характеристик (блок 10). Наиболее приемлемой формой комбинированного прогноза является, на наш взгляд, композиция законов распределения с учетом весовых коэффициентов γ_i каждого из непротиворечивых вариантов. Воспользовавшись символической записью для композиции законов распределения" запишем в общем виде выражение для плотности распределения комбинированного прогноза

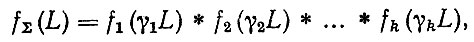
где * - символ композиции; k - число непротиворечивых вариантов прогноза; γ_i - весовые коэффициенты, Σγ_i = 1.

Расчет f_Σ(L) производится по рекуррентной формуле

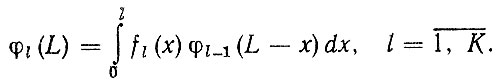(2.75)

Учитывая сложность расчетов по формуле (2.75), для определения f_Σ(L) целесообразно использовать метод статистических испытаний. При моделировании случайные значения ресурсов ξ_Σj, соответствующие комбинированному прогнозу, рассчитываются по формуле

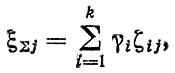(2.76)

где ξ_ij - случайная величина ресурсов i-го варианта прогноза. Дальнейшая статистическая обработка случайных величин позволяет определить параметры и плотность распределения f_Σ(L). В частности, среднее и среднее квадратическое отклонения комбинированного прогноза находятся по формулам!

(2.77)

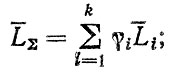(2.77)

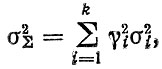(2.78)

где L_i, σ_i - среднее значение и среднее квадратическое отклонение ресурса t-го варианта прогноза.

Одним из наиболее сложных вопросов при составлении комбинированного прогноза является выбор весовых коэффициентов. Они могут быть определены различными способами: с учетом мнений экспертов, пропорционально ошибкам вариантов прогноза и т. п. Например, для получения минимальной дисперсии комбинированного прогноза предложена формула

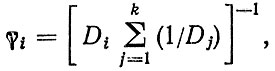(2.79)

где D_j - дисперсия j-го варианта прогноза.

Однако условие минимальной дисперсии комбинированного прогноза может привести к смещенной оценке его среднего значения. Помимо этого, в условиях отмечавшейся ранее природной неопределенности учет того или иного числа факторов в логической модели расчета ресурса детали может привести к различным оценкам весового коэффициента. При этом будет наблюдаться обратная картина: чем больше факторов учтено и, следовательно, дисперсия больше, тем меньше весовой коэффициент. Очевидно, другой вариант оценки весовых коэффициентов по дисперсиям может быть записан в виде

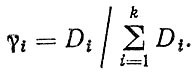(2.80)

Таким образом, приведенная методика позволяет получить параметры комбинированного прогноза с оценкой непротиворечивости вариантов; накопление опыта расчетов по методике даст возможность уточнить некоторые положения, в частности выбор весовых коэффициентов.