2.5. Прогнозирование показателей ресурса деталей на основе ретроспективной информации

Рассмотренные модели расчета ресурса деталей, основанные на физике отказов, формально не учитывают накопленную информацию о ресурсах ранее выпущенных изделий и с точки зрения прогнозирования могут быть отнесены к эвристическим (интуитивным) методам. Известно, что по сравнению с экстраполяционным эвристические методы позволяют предсказать качественные скачки в развитии, например увеличение ресурса при разработке новой конструкции или ее модернизации. В то же время представляет интерес разработка методики прогнозирования ресурса деталей без составления логической модели, но с учетом накопленной информации об эксплуатации (испытаниях] ранее выпущенных машин-аналогов.

Проведенные исследования показали, что для деталей автомобиля такие оценки могут быть получены с помощью корреляционных уравнений долговечности (КУД), отражающих связь между выбранными критериями А_п, характеризующими нагрузочный режим, и данными о ресурсах деталей" полученными в результате наблюдений за эксплуатацией подконтрольных групп автомобилей [17, 24, 25]. Если воспользоваться кибернетической схемой "черного ящика", то речь идет об установлении функции отклика между "входами"-факторами и "выходами"-параметрами, один из которых отражает ресурс детали.

Один из возможных вариантов критерия с учетом влияния на долговечность условий эксплуатации можно представить в виде суперпозиции распределений

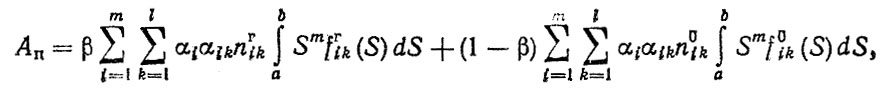(2.63)

где β - коэффициент использования пробега; α_i - коэффициент, учитывающий распределение пробега автомобиля по типам дорог,

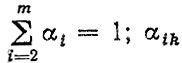
коэффициент, учитывающий распределение пробега автомобиля по "элементарным:" нагрузочным режимам (т. е. трогание, разгон, установившееся движение, торможение и др.), характерным для данной детали,

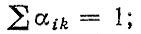
n⁰_ik, n^г_ik интенсивности k-го "элементарного" для данной детали нагрузочного режима на i-м дорожном покрытии, соответственно для не груженого и груженого автомобилей; f_ik⁰ (S), f_ik^г (S) - плотности распределения k-го "элементарного" нагрузочного режима на i-м дорожном покрытии соответственно для не груженого и груженого автомобилей.

В формуле (2.63) обобщенный нагрузочный режим представлен в виде сумм плотностей распределений элементарных нагрузочных режимов f_ik⁰ (S) и f^г_ik (S), определяемых путем обработки статистических данных дорожных испытаний автомобилей или аналитически.

Накопленный опыт построения КУД для деталей двигателей, трансмиссии, подвески позволил сформулировать основные положения методики прогнозирования показателей ресурса, которая представлена в виде блок-схемы на рис. 2.11.

В зависимости от наличия исходной информации методикой предусматривается три варианта корреляционных уравнений долговечности: первый - КУД без учета временного тренда; второй - КУД с учетом временного тренда; третий - КУД с учетом временного тренда и корректировкой по результатам испытаний новых изделий.

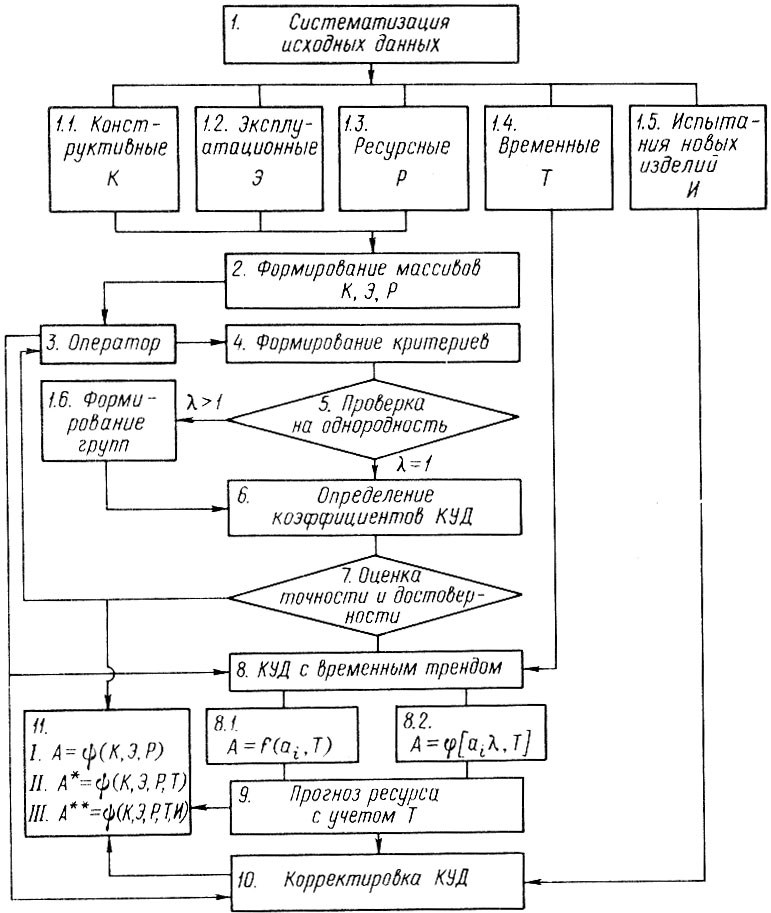
Рис. 2.11. Схема прогнозирования ресурса деталей с использованием корреляционных уравнений долговечности

В блоке 1 производится систематизация исходных данных о подконтрольных партиях автомобилей» которые подразделяются на конструктивные (размеры» материалы)» эксплуатационные (условия эксплуатации)» ресурсные (ценки параметров: средние значения, дисперсии и т. п.), временные (учитывают время выпуска или модернизации изделий), а также включают результаты испытаний новых изделий, если они получены на момент разработки прогноза. На основании исходных данных (блоки 1.1, 1.2 и 1.3) формируются массивы для последующей обработки в случае использования ЭВМ (блок 2).

Поскольку процедура поиска КУД в настоящее время полностью не формализована, то одним из основных элементов методики является наличие оператора (блок 3), который принимает решения о формировании критериев A_i (блок 4) и возможных вариантах КУД (блоки 8, 10).

Для повышения точности КУД необходимо проводить оценку однородности полученных в результате расчетов критериев A_i (блок 5). Это может быть выполнено различными способами, в частности, с использованием теории распознавания образов [57, 64 ]. Если исходные данные могут быть сформированы в группы, относящиеся к различным поколениям автомобилей, то целесообразно искать КУД для каждой группы раздельно (блок 5.1). Так в работе [42] в одну группу были объединены данные по двигателям ЗИЛ-164, ЗИЛ-158, ГАЗ-51 и др., выпущенным в 50-х годах, во-вторую - по двигателям ЗИЛ-130, ЗИЛ-575, ГАЭ-53, ЯМЗ-286 и т. д., выпущенным в 60-х годах.

При выборе модели КУД необходимо обратить внимание на следующие факты. Например, при испытаниях на усталость между нагрузкой (амплитудами напряжений S) и ресурсом (числом циклов до поломки N) имеет место гиперболическая зависимость

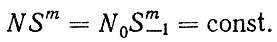(2.64)

Аналогичная зависимость наблюдается и при износе" Так, для веерной функции (2.4) можно записать

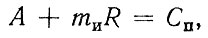(2.65)

где m_и - скорость изнашивания; С_п - предельный износ.

Если в формулах (2.64), (2.65) сомножители S, m_и рассматривать как критерий нагруженности, a N, R - как ресурс, то можно сделать вывод, что модели КУД должны удовлетворительно описываться зависимостями:

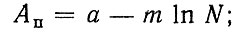(2.66)

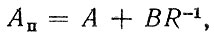(2.67)

т. е. гиперболической (2.67), логарифмической (2.66) и т. п.

Для нахождения коэффициентов уравнений (2.66), (2.67) наиболее приемлемым является метод наименьших квадратов (МНК). Учитывая, что модели КУД являются нелинейными и для них нельзя получить систему так называемых нормальных уравнений, то для нахождения коэффициентов следует использовать либо специальные методы, например, градиентный, случайного поиска ит. п., либо воспользоваться подстановками типа R^-1 = 2, In N = z, позволяющими привести зависимости (2.66), (2.67) к линейному виду.

Оценка точности и достоверности является последним этапом при использовании КУД для прогнозирования ресурса в первом варианте, т. е. без учета временного тренда (блок 7). Для оценки достоверности могут быть использованы различные статистические характеристики [57]: стандартная ошибка, средняя относительная ошибка, корреляционное отношение, F - критерий Фишера и др. В данной методике для оценки достоверности КУД используется коэффициент множественной корреляции

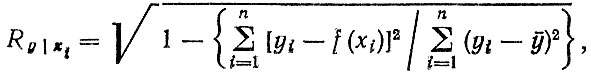(2.68)

где y_i - значения зависимой переменной (критерий долговечности); f (x_i) - уравнение множественной регрессии, коэффициенты которого определены с использованием МНК; ȳ - среднее значение,

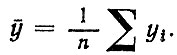
Если независимая переменная одна - уравнения (2.66), (2.67), то формула (2.68) позволяет оценить корреляционное отношение η_x|y. Очевидно, чем меньше отклонение y_i от подобранной зависимости f (x_i), тем интенсивнее корреляция, а значения R_y|xi (и соответственно η_y|x) ближе к единице. Это позволяет за счет обратной связи в схеме осуществить выбор такого критерия A_п, при котором R_y|xi (или η_y|x) достигает максимального значения. По корреляционному уравнению, соответствующему R_y|xi = max, производится прогноз параметров ресурса (блок 11); в этом случае временной тренд присутствует неявно (первый вариант прогноза).

Оценка точности прогноза помимо описанной в литературе процедуры, основанной на теории обучения машин [57], производится с помощью доверительного интервала. Считают, что чем уже доверительный интервал, тем точнее прогноз.

Для уравнений типа (2.66)-(2.67), преобразованных путем подстановок z = x^-1 или z = ln x к линейному виду y(z) = a + bz доверительные границы определяются по формуле

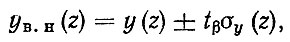(2.69)

где t_β - статистика Стьюдента; σ_y (z) - среднее квадратическое отклонение функции.

Величину σ_y (z) можно найти методом линеаризации:

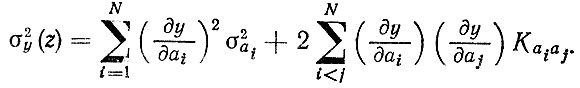(2.70)

Для линейного варианта (N = 1) получим [63]

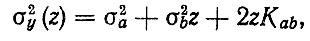(2.71)

где

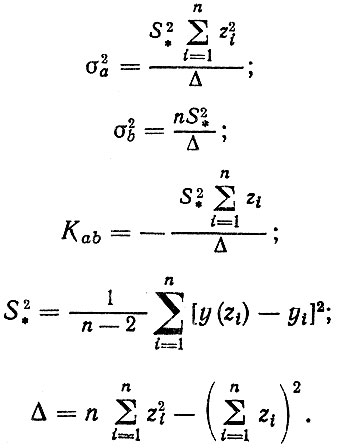(2.72)

В блоке 8 производится определение коэффициентов КУД с учетом временного тренда. Анализ показал, что здесь возможны два типа зависимостей: в виде множественного корреляционного уравнения, когда одним из факторов является время начала выпуска Т (или модернизации) детали (блок 8.1); когда исходная информация разбита на группы, соответствующие определенным периодам развития автомобильных конструкций (блок 8.2). В этом случае временной тренд учитывается в виде корреляционных уравнений для коэффициентов КУД. Например, для зависимости (2.67) имеем

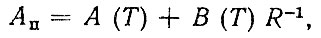(2.73)

где А (Т), В (Т) - корреляционные уравнения, рассчитанные на основе A_λ и B_λ для различных групп.

Прогноз параметров ресурса R^* выполняется на основе прогнозного значения критерия A^* и выбранного интервала упреждения Г^* (блок 9). Доверительный интервал прогноза рассчитывается по формулам, аналогичным (2.69) и (2.72).

В методике предусмотрена корректировка КУД с временным трендом по результатам испытаний новых изделий (блок 10). Для этого может быть использовано дисконтирование, т. е. уменьшение ценности ранней информации по сравнению с более поздней, а также методы адаптивного экспоненциального сглаживания [57, 73]. В частности, при дисконтировании расчет коэффициентов КУД с использованием МНК производится с учетом весовых коэффициентов β_i ≤ 1, при этом для ранних значений β_i ≈ 0, тогда как результаты испытаний новых изделий вводятся о коэффициентом β_i ≈ 1.

Необходимо отметить, что при прогнозировании по КУД можно получить неверные результаты, если рассматриваемая деталь качественно отличается по конструктивным или технологическим параметрам. В этом случае переход к новой технологии или конструкции должен быть учтен при расчете критерия долговечности введением поправочных коэффициентов.

При построении КУД для одной марки автомобиля можно ожидать повышения точности расчетных оценок средних ресурсов.