2.4. Логические модели отказов деталей

Если деталь отказывает из-за одного дефекта, наблюдающегося в одном из ее элементов (сечений), то приведенные в пп. 2.1-2.3 расчетные модели позволяют оценить показатели ее надежности. Однако для большинства деталей, особенно сложной конфигурации, а также для некоторых элементов характерно протекание нескольких разрушительных процессов, приводящих к отказу детали, В этом случае все попытки рассчитать ресурс детали, выделив только один из разрушительных процессов, не дают положительных результатов. Вследствие этого для совершенствования методов расчета ресурса необходимо, основываясь на анализе причинно-следственных предпосылок отказов, разрабатывать логическую модель отказа детали. Следует подчеркнуть, что этот вопрос практически не нашел отражения в литературе, за исключением классического примера, когда элемент (деталь) выходит из строя из-за внезапного и постепенного отказов, подчиняющихся соответственно экспоненциальному и нормальному законам [55]. В этом случае вероятность безотказной работы Р (t) при условии независимости указанных отказов определяется по формуле

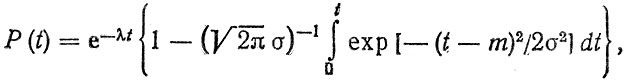(2.47)

где λ - параметр экспоненциального закона; m, σ - параметры нормального закона.

Выполненный анализ результатов наблюдений за отказами деталей в эксплуатации показал, что в основу моделей отказов деталей могут быть положены три типа зависимостей между разрушительными процессами:

первый - разрушительные процессы x_i(t)f протекающие в различных сечениях детали (или в одном сечении), приводят к возникновению независимых отказов;

второй - разрушительные процессы y_i(t), не приводящие к отказу при достижении предельных состояний, являются причинами возникновения других процессов x_i(t), приводящих к отказам;

третий - разрушительные процессы x_i(t), приводящие к отказам, развиваются в зависимости от того, достигают ли определенного состояния другие разрушительные процессы y_i (t), не приводящие к отказу.

Рассмотрим подробнее каждую из указанных типов зависимостей.

Первый тип. В сечении или в нескольких сечениях детали протекает N разрушительных процессов, каждый из которых может привести к отказу детали, с плотностью распределения f_i (t). Соответственно вероятности отказов определяются функциями распределения F_i (t), а вероятности безотказной работы P_i (t) = 1 - F_i (t). Поскольку по условию вероятности событий наступления отказов независимы, то на основе теоремы умножения вероятностей можно записать выражение для вероятности безотказной работы детали

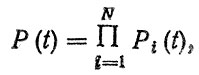(2.48)

и вероятности отказа

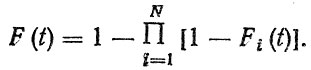(2.49)

Для нахождения плотности распределения ресурса f (t) необходимо продифференцировать F (t) по времени. Расчетную формулу для f (t) удобно записать в виде [10]

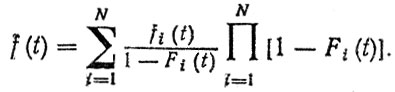(2.50)

Приведенные формулы (2,49), (2,50) описывают функцию и плотность распределения минимальных значений для N случайных величин; модель отказа деталей первого типа соответствует схеме последовательного соединения элементов [60, 70].

Пример, Рассчитаем показатели ресурса полуоси, отказы которой происходят по двум независимым причинам: усталости и износу. Усталостные отказы имеют место по телу и шлицам и подчиняются распределению Вейбулла

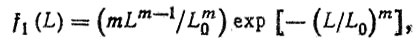(2.51)

где m = 1,5, L₀ = 170; соответственно среднее значение L₁ = 145 тыс. км, среднее квадратическое отклонение σ₁ = 100 тыс. км.

Износные отказы наблюдаются по шлицам под полуосевые шестерни в подчиняются нормальному закону распределения

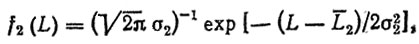(2.52)

где L₂ = 200 тыс. км, σ₂ = 40 тыс. км.

Плотности распределения f₁(L) и f₂ (L) определяются о использованием моделей рассмотренных в пп, 2.1, 2.2.

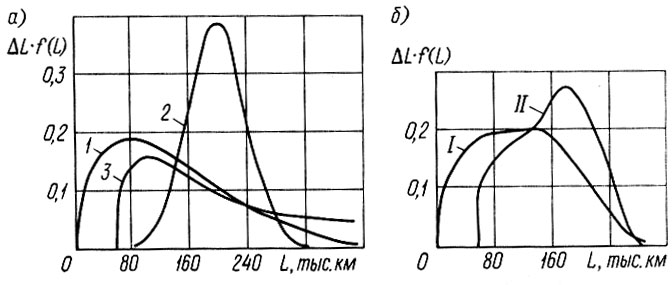
Рис. 2.9. Определение ресурса полуоси при усталостных и износных отказах (ΔL = 40 тыс. км): а - распределения наработок до отказа по усталости и износу; б - распределение ресурса при совместном действии усталости и износа; 1, 2, 3 - распределения Вейбулла f₁(L), нормальное f₂(L) и экспоненциальное f₃(L) соответственно; I, II - варианты расчета f_I(L) и f_II(L)

При подстановке (2.51), (2.52) в формулу (2.50) находим плотность распределения ресурса полуоси

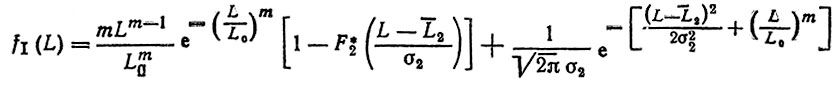(2.53)

и функцию распределения

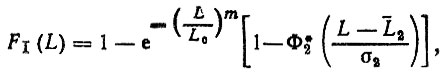(2.54)

где

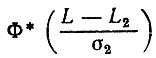
- интеграл вероятностей [14].

Результаты расчетов f₁ (L), f₂ (L) и f_I (L) приведены в табл. 2.5, а также на рис. 2.9; средний ресурс полуоси поставил L_I = 131 тыс. км. Поскольку сомножители вида [1 - F_i (L)] характеризуют вероятность безотказной работы, то первое слагаемое в формуле (2,53) определяет долю отказов от усталостных поломок, а второе - от износа. Так, в рассматриваемом примере на долго усталостных поломок приходится 71% всех отказов.

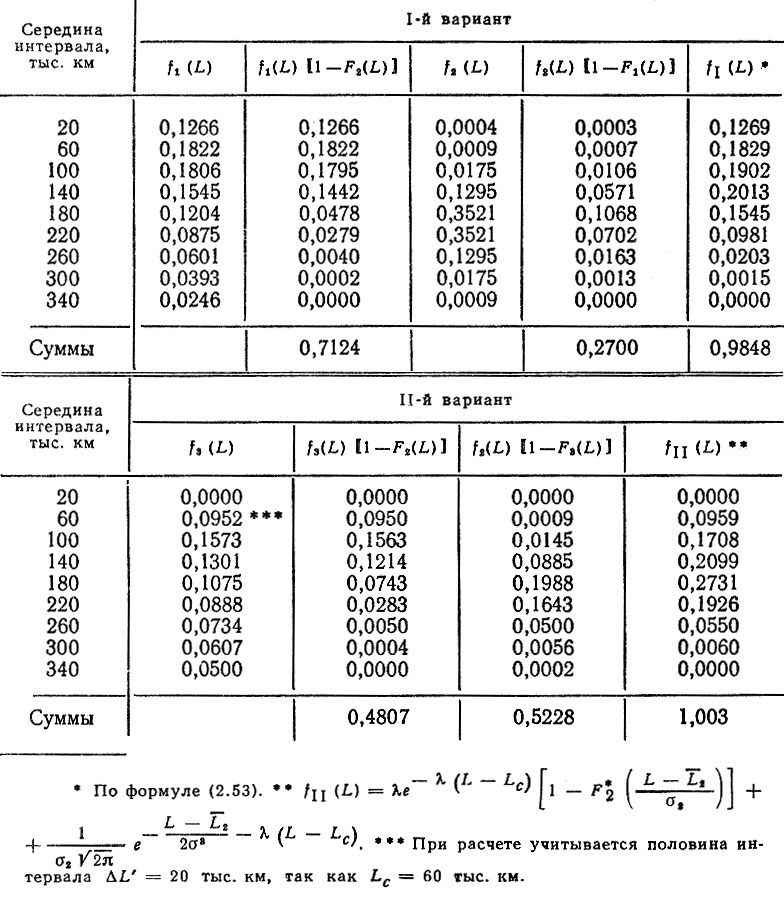
Таблица 2.5. Расчет плотности распределения ресурса полуоси (при наличии усталостных и износных отказов)

Допустим, что в результате замены материала и изменения технологии упрочнения удалось повысить только усталостные характеристики полуоси; плотность распределения ресурса (по усталости) в этом случае подчиняется двух параметрическому экспоненциальному закону

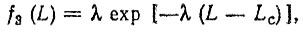(2.55)

где

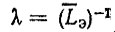
- параметр распределения; L_Э = 210 тыс" км; L_c - параметр сдвига, L_c =60 тыс. км-.

Следовательно, средний ресурс полуоси по усталости L₃ = L_Э + L_c = 270 тыс. км, т. е. превосходит средний ресурс L_II = 145 тыс. км почти в два раза.

На рис. 2.9 приведены плотности распределения f₃ (L) и f_II (L). Доля усталостных отказов уменьшалась до 48% (см. табл. 2.5), но средний ресурс полуоси - L_II = 161 тыс. км, т. е. увеличился только на ΔL = (161 - 131)/131 = 21%. Таким образом" увеличение среднего ресурса (даже многократное) одного из сечений не всегда приводит к пропорциональному росту среднего ресурса детали, у которой наблюдается несколько разрушительных процессов.

Частным случаем зависимостей (2.49), (2.50) являются выражения для функции и плотности распределения минимальных значений случайных величин, подчиняющихся одному закону распределения (см. табл. 2.2), Приведенные в табл. 2.2 формулы следует использовать при оценке ресурсов деталей, имеющих одинаковые размеры отдельных элементов (сечений), когда получено распределение ресурса для всей совокупности элементов. Следует подчеркнуть, что в конструкции автомобиля имеется значительное число деталей и сборочных единиц, при расчете которых можно использовать формулы для минимальных значений, например детали - коленчатые валы (шатунные, коренные шейки), распределительные валы (кулачки, опоры), крестовины карданных шарниров и дифференциала, вилки карданов и др.; сборочные единицы - сателлиты дифференциала и колесной передачи, подшипники крестовины, пружины сцепления (нажимные, демпфера) и др.

Второй тип. Допустим, что в сечении детали могут протекать два разрушительных процесса х(t) и y(t), при этом процесс х (t) приводящий к отказу, начинает развиваться только после того, как процесс y (t) достигает своего предельного значения. К зависимостям второго типа относятся такие сочетания процессов, как "статическая прочность - мало(много)цикловая усталость, "износ - усталость (прочность)", "усталость - прочность" и т. п.

Очевидно, для определения случайной величины ресурса необходимо рассмотреть сумму случайных величин

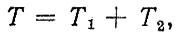(2.56)

где Т₁ - случайная величина наработки до предельного состояния, определяемая процессом y(t); Т₂ - случайная величина наработки до отказа.

Если величины Т₁ и Т₂ зависимые и подчиняются двумерной плотности распределения φ = (T₁, T₂), то

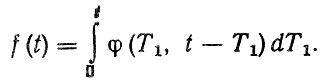(2.57)

Если случайные величины T₁ и Т₂ независимы и описываются плотностями распределения f₁ (t₁) и f₂ (t₂), то для расчета используется формула композиции законов распределения

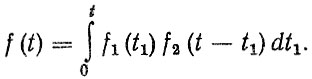(2.58)

При сопоставлении формулы (2.58) с результатами, полученными, например, в работе 120], следует, что она соответствует невосстанавливаемой системе с ненагруженным (холодным) резервом, включающей основной и резервный элементы (при мгновенном срабатывании переключателя).

Пример. При наличии упрочненного слоя толщиной С_у реализации износа описываются функцией вида (2.4) S (t) = S₁t, где S₁ - случайная величина скорости изнашивания, подчиняющаяся нормальному закону распределения с параметрами S₁ и σ_S1. Когда упрочненный слой изнашивается, реализации износа также подчиняются зависимости (2.4), при этом средняя скорость изнашивания

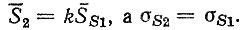
Предельная величина износа, при которой наступает отказ детали, равна С_п.

Для расчета параметров плотностей распределения f₁(t) и f₂ (t), т. е. наработок до износа упрочненного слоя С_у и предельного износа С_п воспользуемся формулами (2.21). При подстановке исходных данных находим средние значения

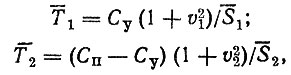
средние квадратические отклонения

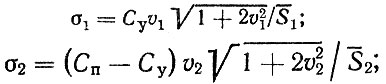
где v₁ = σ_S1/S₁; v₂ = σ_S1/S₂.

Допустим, что законы распределения f₁ (t₁) и f₂ (t₂) - нормальные, а случайные величины Т₁ и Т₂-независимые. Тогда, плотность распределения ресурса f(t) будет также подчиняться нормальному закону

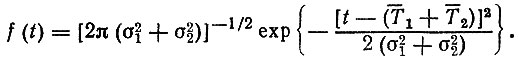
На рис. 2.10 приведены результаты расчета f₁ (t₁) и f(t) при следующих исходных данных: S₁ = 1,1 мкм/тыс. км; S₂ = 1,54 мкм/тыс. км; σ_S2 = 0,4 мкм/тыс. км; С_у = 200 мкм; С_п = 300 мкм.

Третий тип. Для описания зависимостей третьего типа введем следующие допущения:

отказ детали определяется достижением предельного состояния процессом х (t) на отрезке 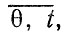наработка на отказ подчиняется

плотности распределения f_x (t); одновременно протекает второй процесс y (t), не приводящий к отказу, наработка до предельного состояния процесса y (t) подчиняется плотности распределения f_y (t);

при достижении процессом y (t) предельного состояния в момент τ < t изменяется характер протекания процесса х (t), наработка до отказа детали описывается условной плотностью распределения f_x|y (t, τ) = f_xy (t, τ)/f_y (τ).

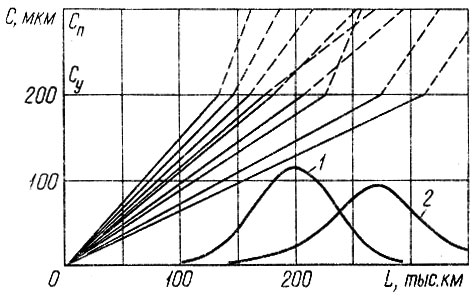
Рис. 2.10. К расчету ресурса, детали по износу при наличии упрочненного слоя: 1 - распределение наработки до износа упрочненного слоя С_у; 2 - распределение наработки до отказа

Для нахождения функции распределения ресурса детали воспользуемся формулой полной вероятности

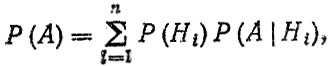(2.59)

где Р (Н_i) - вероятность гипотезы Н_i; Р (А |H_i)- условная вероятность события A при этой гипотезе.

Очевидно, в данном случае можно рассмотреть две гипотезы, характеризующие состояние детали в момент τ < t:

H₁ - процесс y(t) не достиг предельного состояния

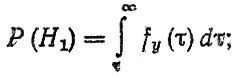
Н₂ - процесс y(t) достиг предельного состояния.

При гипотезе Н₁ вероятность отказа не зависит от Y(t), т. е. Р (А | Н₁) = Р (А), и определяется протеканием процесса x (t). Тогда

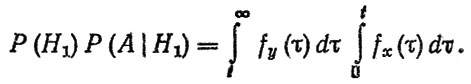(2.60)

При гипотезе H₂ условная вероятность

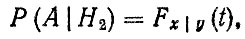
следовательно,

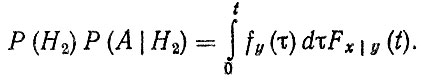(2.61)

При подстановке (2.60) и (2.61) в формулу (2.59) находим вероятность отказа детали

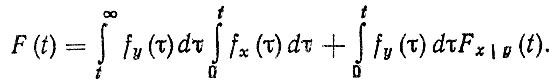(2.62)

Таким образом, для расчетов ресурсов деталей с использованием формулы (2,62) необходимо знать условную функцию распределения F_x|y(t), определение которой требует проведения соответствующих экспериментов. В большинстве случаев вместо расчетов по формуле (2.62) удобнее воспользоваться методами статистических испытаний, моделируя процессы x (t) и y (t).

На основании вышеизложенного сформулируем основные этапы методики расчета ресурса детали.

1. Выявление сечений (элементов) детали, которые должны подвергаться расчету на долговечность. Для деталей, имеющих аналоги, за основу принимаются результаты испытаний, эксплуатационных наблюдений и микрометрирования (главным образом при капитальном ремонте). Для вновь проектируемых деталей выбор осуществляется но результатам экспертного опроса"
2. Определение преобладающих видов разрушительных процессов для каждого сечения (износ, усталость и т. п.); выбор расчетных моделей и оценка взаимосвязи между процессами.
3. Определение исходных данных для расчета плотностей распределений, главным образом на основе методов прогнозирования, отдельных сечений детали,
4. Формирование логической модели ресурса детали; оценка показателей ресурса детали.