
2.3. Методы расчета на статическую прочность
Рассмотрим случай, когда функции распределения прочности (несущей способности) FR (R) и нагрузки FS (S) описывают положительные случайные величины с параметрами сдвига (рис. 2.6).
Для учета этих параметров необходимо обратиться к общей формуле (1.17), которая может быть представлена в виде
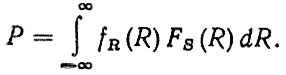 (2.34)
(2.34)Тогда о учетом параметров сдвига Rc и Sc выражение (2.34) примет вид
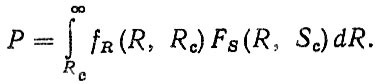 (2.35)
(2.35)
Если параметр сдвига учитывается только в одной из функций распределения, как правило прочности FR (R, Rc), то
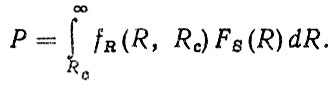 (2.36)
(2.36)
Допустим" что Fs (S) и FR (R) описываются экспоненциальными законами распределения
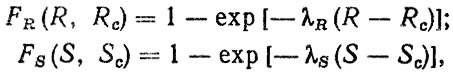
где λR, λS - параметры распределений.
При подстановке FR (R, Rc), FS (S, Sc) в формулу (2,35) после преобразований получим
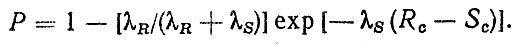 (2.37)
(2.37)Если Sc = 0, т. e. функция распределения нагрузки не имеет параметра сдвига
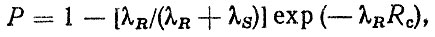
при Sc = Rc = 0 [38, 69]
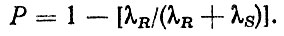
Таким образом, формула (2.35) позволяет получить расчетные зависимости для физически обоснованных распределений прочности и нагрузки, подчиняющихся случайным положительным величинам с параметрами сдвига (табл. 2.1).
Следует подчеркнуть, что к модели расчета на статическую прочность сводятся и расчеты на усталостную долговечность в случае, если плотность распределения нагрузочного режима расположена значительно ниже плотности распределения предела выносливости f(S-1) (рис. 2.7). Поскольку теоретически f(S-1) описывается законами распределения с параметрами сдвига" например трехпараметрическим распределением Вейбулла [30], а распределение амплитуд является распределением положительных случайных величин, то расчет вероятности безотказной работы производится по формуле (2.35).
При использовании моделей расчета на статическую прочность обычно не оговаривается, каким образом получен закон распределения нагрузок, и принимается, что его параметры не зависят от продолжительности работы конструкции. Такое допущение оправдано для максимальных (пиковых) нагрузок, которые могут возникнуть в экстремальных условиях эксплуатации ("наихудший" случай). Например, в трансмиссии автомобиля такие нагрузки возникают при броске педали механического сцепления при троганни в тяжелых дорожных условиях; в рулевом управлении, подвеске при ударе передними колесами о вертикальное препятствие или попадании в яму и т. д. Следовательно, максимальные нагрузки возникают в случайные непредсказуемые моменты времени и практически не связаны с продолжительностью эксплуатации.
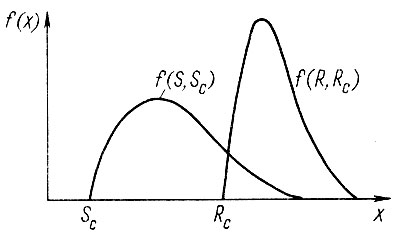
Рис. 2.6. К расчету на статическую прочность с учетом распределений нагрузки f(S, Sc) к прочности f(R, Rc), имеющих параметр сдвига
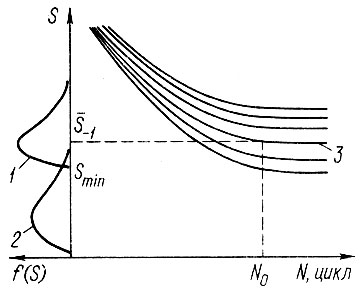
Рис. 2.7. К расчету на усталостную долговечность: 1 - распределение предела выносливости f (S-1) с параметром сдвига Smin; 2 - распределение амплитуд нагрузки f (S); 3 - кривая усталости N (S), соответствующая вероятности не разрушения Р = 50%
Рассмотрим другой возможный вариант определения функции распределения нагрузок F (S), основанный на зависимостях для максимальных (минимальных) значений случайных величин. Известно, что для независимых случайных величин, подчиняющихся одному и тому же закону распределения, справедливы соотношения для функций и плотностей распределения максимальных (минимальных) величин (табл. 2.2), которые могут быть использованы для непосредственных расчетов при небольших n. При n → ∞ наблюдаются три типа предельных распределений [6, 14].

Таблица 2.1. Формулы для расчета вероятности безотказности работы при статическом нагружении
Для расчетов на статическую прочность наибольший интерес представляют распределения типов I и III (табл. 2.3).
Допустим, что при эксплуатации на пробеге LА зафиксированы максимальные нагрузки Smax, превышающие некоторую величину SA. Полученные значения статистически обрабатываются, и находится закон распределения F (Smax). Для определения закона распределения Fn (Smax) на пробеге 2LA, 3LA, .... nLA используются зависимости для максимальных (предельных) значений случайных величин (см. табл. 2.2). Затем с помощью распределения Fn (Smax) при различных n определяется вероятность безотказной работы Р (L), соответствующая пробегу nLA (рис. 2.8).
В некоторых случаях могут оказаться полезными следующие формулы. Если F (Smax) подчиняется нормальному закону распределения с параметрами Smax и σSmax и не ограничена сверху, то предельным является распределение I-го типа (см. табл. 2.3), плотность которого
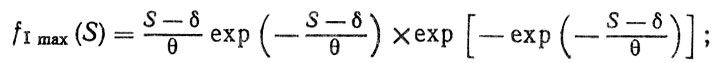 (2.38)
(2.38)параметры δ и θ определяются с помощью асимптотических формул [9]:
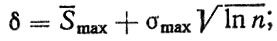 (2.39)
(2.39)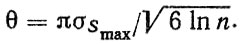 (2.40)
(2.40)Если F (Smax) подчиняется закону Вейбулла с параметрами m, S0 и ограничена сверху значением Sп, то предельным является распределение 11I-го типа (см. табл. 2.3)
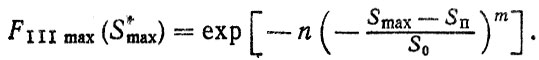 (2.41)
(2.41)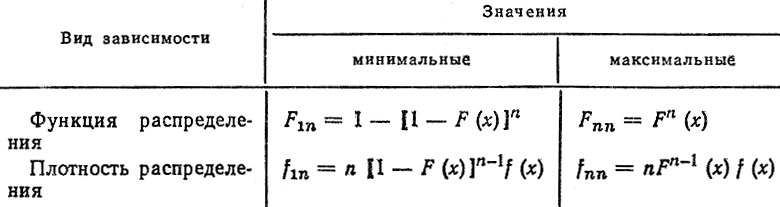
Таблица 2.2. Распределение минимальных и максимальных значений случайных величин
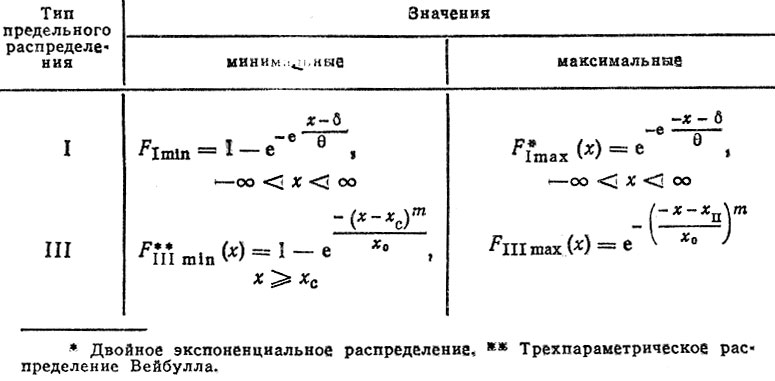
Таблица 2.3. Функции распределении предельных значений случайных величин
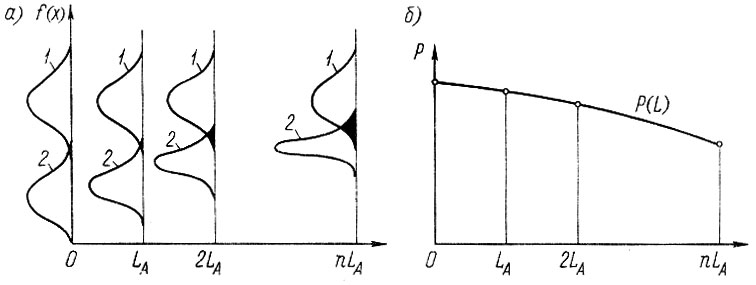
Рис. 2.8. К расчету на статическую прочность с учетом изменения закона распределения нагрузки: а - формирование предельных нагрузок в зависимости от пробега; б - вероятность безотказной работы; 1 - распределение прочности t(R); 2 - распределение нагрузки fn (Smax)
Для некоторых деталей, например ходовой части автомобиля, нагрузочные режимы описываются с помощью нормальных стационарных случайных процессов, В этом случае плотность распределения предельных значений (абсолютного максимума)
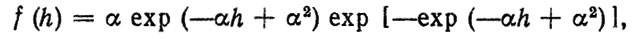 (2.42)
(2.42)где
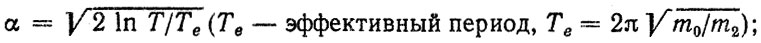
m0, m2 - моменты спектральной плотности стационарного случайного процесса; Т - длина реализации процесса, с; h = Smax/σS; σS - среднеквадратическое отклонение.
Нетрудно заметить, что формулы (2.38) и (2,42) аналогичны. Последняя соответствует центрированному процессу, т. е. ms = 0, Следовательно, при установлении зависимости между Т и nLА можно определить и зависимость вероятности безотказной работы Р (L) от пробега.
При расчетах можно воспользоваться другой зависимостью для абсолютного максимума [6]
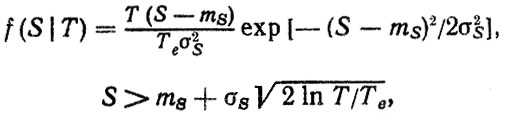 (2.43)
(2.43)
где ms, σs - среднее значение и среднее квадратическое отклонение нормального стационарного процесса.
По Р (L) определяется функция распределения отказов, плотность распределения и другие показатели долговечности (средний ресурс, гамма-процентный и т. д.).
Логическим завершением рассмотренных методов расчета является, на наш взгляд, их классификация. Общая классификация вероятностных моделей расчета ресурса на износ, усталость и статическую прочность возможна, так как в основу моделей положен принцип однократного достижения нагрузкой или накопленным повреждением предельного состояния. Основным классификационным признаком может быть выбрано описание нагрузки и предельного состояния, которые соответственно представляются в виде величин (детерминированных, случайных) или процессов (стационарных, нестационарных). При этом необходимо подчеркнуть, что речь идет о простых моделях расчета, в которых нагрузка и предельное состояние - независимые величины или процессы.
Детерминированные величины представляются константами с = const или функциями φ (t). Случайные величины описываются с помощью функции распределения F (x), а также распределениями экстремальных значений (см. табл. 2.3), функциями распределения минимумов Fmin (x) - для предельных состояний и максимумов Fmax (x) - для нагрузки при расчетах на статическую прочность.
Стационарные случайные процессы используются для описания нагрузок в расчетах на усталость, при этом функции распределения выбросов FB (х) (абсолютный максимум) могут быть применены в расчетах на статическую прочность. Нестационарные процессы разделяются на процессы с "сильным" и "слабым" перемешиванием. Для описания нагрузок используются оба вида процессов, для предельных состояний - процессы со "слабым" перемешиванием.

Таблица 2.4. Классификация моделей для расчета показателей надежности деталей
Для классификации расчетных моделей возможные сочетания нагрузок и предельных состояний целесообразно представить в виде таблицы (табл. 2.4). Модель 1.1 - "коэффициент запаса n" - получила наибольшее распространение в практике расчетов машиностроительных конструкций на статическую прочность. Разновидностью этой модели является формула С. В. Серенсена для оценки усталостной прочности
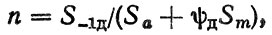 (2.44)
(2.44) где S-1д - предел выносливости детали; Sa, Sm - соответственно амплитуда и среднее значение цикла переменной нагрузки; - коэффициент.
Модели 1.2, 2.1. и 2.2 в отличие от модели 1.1 позволяют получить оценку вероятности отказа R или вероятности безотказной работы Р = 1 - R. Случайные величины нагрузки и прочности представлены в виде функций F (х) или плотностей распределения f (х). Поскольку вид расчетных зависимостей не меняется, то при описании нагрузки и прочности могут быть использованы предельные распределения для максимальных и минимальных величин"
Модели 1.3, 2.3 принципиально отличаются от моделей 1.1 - 2.2 за счет учета связи между функцией распределения максимумов нагрузки Fn (Smax) и временем (пробегом) эксплуатации детали Т. При этом для аналитического описания Fn (Smax) используются асимптотические формулы (2.38), (2,41) или выражения для абсолютного максимума [формулы (2.42), (2.43)]. Например, для нормального стационарного процесса со средним ms = 0 c использованием модели 2.3 находим
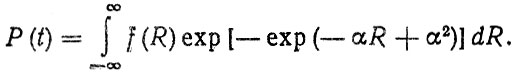
С помощью функции вероятности отказов F (t) = 1 - Р (t) находятся показатели ресурса детали: среднее значение, γ-процентный ресурс, плотность распределения f (t) = dF (t)/dt и др.
Из анализа моделей 1.3, 2.3 следует, что при наличии ограничений на длину реализации T на величину абсолютного максимума Smax и др. полная группа событий будет включать вероятность события Р, не зависящую от времени и характеризующую не разрушение детали, и вероятность события F (f), являющуюся случайной величиной и характеризующую разрушение детали. В этом случае, вероятность события Р совпадает с оценками, получаемыми по моделям 1.2, 2.1, 2.2. Указанная особенность моделей 1.3, 2.3 имеет принципиальное значение при статистической обработке усеченных и многократно усеченных выборок, подразумевающих экстраполяцию функции F (t) для t → ∞, что может привести к существенному искажению показателей ресурса.
Модели типа 1.4, 3.1 получили название "случайный процесс - поле допуска", но для механических систем речь идет, как правило, о достижении реализациями процесса односторонней детерминированной границы. По приведенным формулам рассчитываются плотности распределения ресурсов f (t)> которые позволяют определить другие показатели долговечности и безотказности,
Если предельное состояние описывается не детерминированной, а случайной величиной, то расчеты f (t) могут быть выполнены с использованием моделей 2.4, 3,2. Расчетные формулы получены исходя из того, что модели 1.4, 3.1 рассматриваются как условные плотности распределения f (t|R) или f (t|S). Тогда для независимых случайных величин двумерная плотность распределения, например, ψ(t, R) = f (R) f (t | R), а плотность распределения ресурса
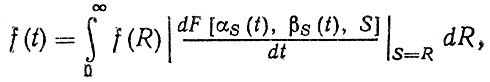 (2.45)
(2.45) где F [αs (t), βs (t), S] - функция распределения реализации процесса, параметры которой αs(t), βs (t) зависят от времени t:
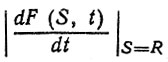
- результат дифференцирования - берется по модулю при подстановке R вместо S.
Другой вариант формул для моделей 2.4, 3.2 может быть получен на основе модели 2.2 в результате подстановки вместо f (S) [или f (R)] плотности распределения f [αs (f), βs (t), S] (или f [αR(t), βR (t), R]) и последующего дифференцирования по t.
В случае, когда нагрузка и прочность являются нестационарными процессами со слабым перемешиванием, переход от "статической" модели 2.2 к "динамической" модели 3.4 осуществляется путем введения в расчетную формулу функций распределения процессов F [αS (t), βS (t), S] и F [αR (t), βR (t), R], зависящих от времени. Например, при подчинении F [αS (t), βS (t), S] и F [ αR (t), βR (t), R ] нормальным законам получим:
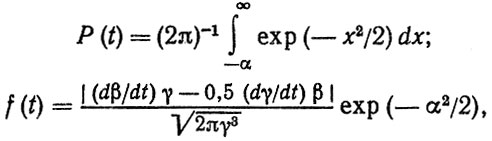 (2.46)
(2.46)
где
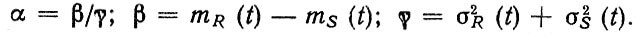
В табл. 2.4 также приведены модели 1.5, 2.5, 3.5 при описании нагрузки нестационарными случайными процессами; основной способ расчета характеристик надежности - статистическое моделирование, которое может быть использовано и при расчетах других моделей.
Таким образом, разработанная классификация моделей для расчета показателей надежности деталей механических систем на износ, статическую прочность и усталость [с учетом формулы (2.5) ] позволяет объединить различные подходы, в частности, такие модели, как "нагрузка - несущая способность", "случайный процесс - поле допуска", получить ряд новых моделей (2.4, 3.2, 3.3, 3.4) и охватывает большинство практически возможных случаев описания нагрузок и предельных состояний; аналитические модели могут быть использованы для разработки комплекта программ расчета в виде отдельных модулей.
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'