
2.2. Методы расчета на усталостную долговечность
Накопленный опыт расчетов на усталостную долговечность деталей механических систем, основанных на линейной гипотезе суммирования повреждений, целесообразно систематизировать в виде бдок-схемы, позволяющей проследить основные этапы расчета, выявить возможные варианты, а также наметить пути дальнейшего совершенствования расчетных методов оценки ресурса элементов конструкций при проектировании.
На рис. 2.4 приведена блок-схема расчета на усталостную долговечность, в которой в соответствии с формулой (1.13), выделены три составляющие: определение и схематизация нагрузочного режима (блоки 1, 2), определение параметров кривой усталости (блок 3) и выбор варианта расчета (блок 4). Из блок-схемы видна многовариантность нахождения каждой из основных составляющих, а также взаимовлияние и взаимосвязь между блоками, возможность проведения независимых (параллельных) расчетов. Рассмотрим подробнее некоторые блоки.
При определении параметров нагрузочного режима возможны три варианта: моделирование, использование методов подобия и корреляции, экспериментальные исследования. При моделировании на вход аналитической модели узла (агрегата), являющейся в общем случае нелинейной и нестационарной, подаются возмущающие воздействия, на выходе получают нагрузочный режим. Для линейных моделей параметры нагрузочного режима могут быть определены с использованием основных положений статистической динамики.
При использовании корреляционных методов предполагается, что результаты ранее проведенных экспериментальных исследований нагрузочных режимов и аналогичных конструкций статистически обработаны в виде множественных корреляционных уравнений, отражающих связь между параметрами нагрузочного режима, основными конструктивными характеристиками и условиями эксплуатаций.
Смоделированные или полученные экспериментально нагрузочные режимы подвергаются схематизации (блок 2), при этом описанные в литературе способы можно свести к двум; с использованием экстремальных точек процесса (максимумов и минимумов); с использованием характеристик случайных процессов.
Способы первого направления характеризуются тем, что не учитывается частотный спектр процесса нагружения и вводится среднее число циклов на единицу пути или времени. Наиболее часто в расчетах используются следующие способы; максимумов, размахов (амплитуд), укрупненных размахов, полных циклов, метод "дождя". Основное преимущество этих способов заключается в том, что они не накладывают ограничений на схематизируемый процесс, т. е. любой нагрузочный режим может быть обработан данными способами.
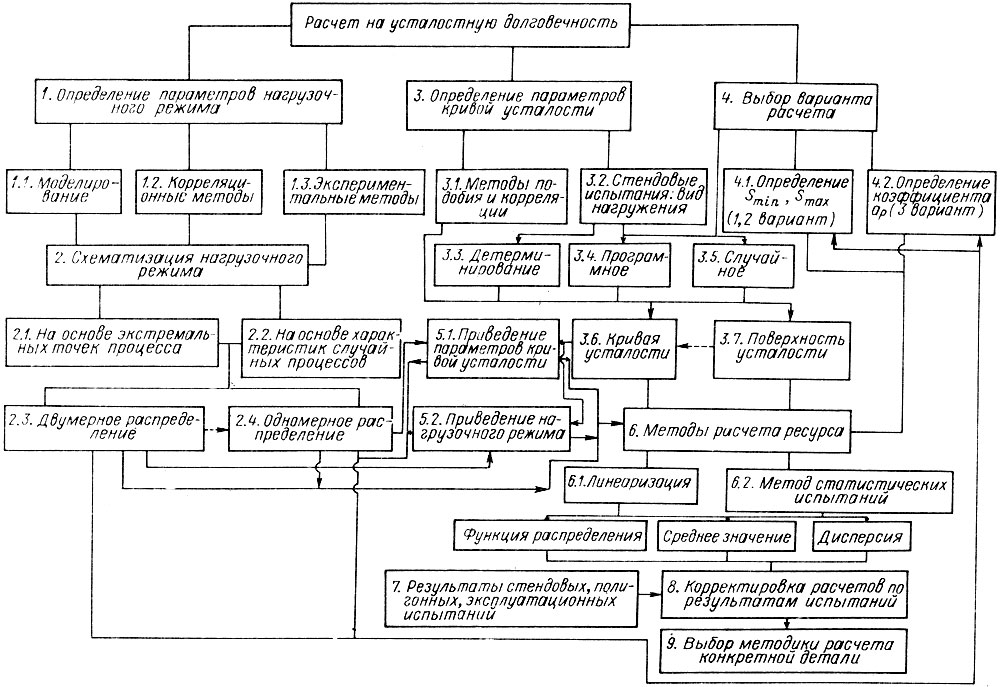
Рис. 2.4. Схема определения усталостной долговечности
Второе направление, основанное на так называемой корреляционной теории случайных функций, получило развитие применительно к нормальным стационарным процессам. При обработке получают одномерную плотность распределения ординат нагрузочного режима, число максимумов и пересечений среднего уровня, плотность распределения максимумов (минимумов) и т, д.
Следует отметить, что для некоторых способов схематизации нагрузочный режим может быть представлен в виде одномерных f (S) и двумерных распределений f (S1, S2). Схематизация в виде двумерных распределений является более трудоемкой, но из нее легко определяются одномерные распределения.
Например, для нормальных стационарных процессов двумерная плотность распределения максимумов-минимумов записывается в виде
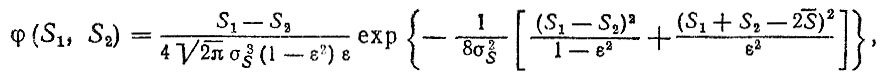 (2.25)
(2.25)
а распределение амплитуд - средних значений
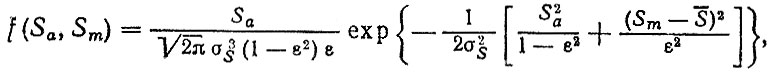 (2.26)
(2.26)где S - среднее значение случайного процесса; σ2S - дисперсия случайного процесса;S1 = Smaxi, S2 = mini - максимальные и минимальные значения i-го цикла; Sa, Sm - амплитуды и средние значения i-го цикла; в - коэффициент узкополосности.
Из двумерного распределения (2.25) находится распределение максимумов (Райса)
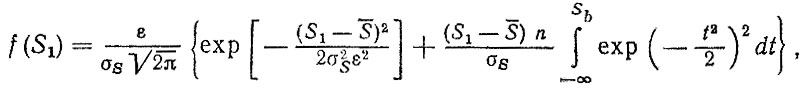
а из (2.26) - распределение амплитуд (Рэлея)
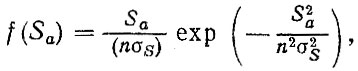
где
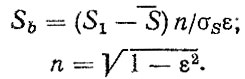
Схематизированные нагрузочные режимы используются непосредственно в расчете и при определении обобщенного нагрузочного режима (блок 2,5), учитываются при определении границ повреждающих напряжений и коэффициента ap, а также при оценке влияния асимметрии на кривую усталости/
Для аналитического описания кривой усталости (блок 3) наиболее часто используется зависимость вида
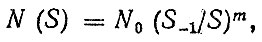 (2.27)
(2.27)
где N0 число циклов, соответствующее точке перелома кривой выносливости (или базовое число циклов); m - параметр кривой.
При использовании в расчетах двумерного распределения нагрузочного режима поверхность усталости может быть записана
в виде
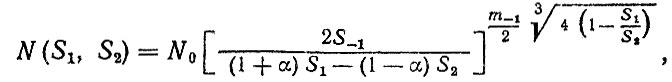 (2.28)
(2.28)где α = S-1/ST, ST - предел текучести; m-1 - параметр кривой усталости при нагружении симметричным циклом; S1 = Smax, S2 = Smin.
Параметры, входящие в формулы (2,27), (2.28), определяются по результатам стендовых испытаний при детерминированном нагружении (блок 3.3). Второй способ получения параметров - использование методов подобия и корреляционных зависимостей - подробно описан в работах [30, 56].
При программном и случайном нагружениях находят вторичную кривую усталости, оценка же параметров кривой, соответствующей детерминированным испытаниям, не производится" При двухступенчатом программном блоке строят кривую повреждаемости. Методика определения параметров кривой усталости N0, m-1 по результатам испытаний при программном или случайном нагружении приведена в работе [41],
В блоке 4 выбирается один из возможных вариантов расчета по гипотезе суммирования повреждений. В блок-схеме рассмотрены три варианта: 1-й вариант - ар = k - 1; 2-й вариант - ap = 1, k = 0,4÷0,6; 3-й вариант - "корректированный", в котором коэффициент ар определяется по формуле (1Л4).
Представленные варианты не охватывают описанные в литера" туре нелинейные варианты гипотезы суммирования повреждения и способы расчета, учитывающие снижение предела усталости.
Для учета асимметрии нагрузочного режима в блок-схеме предусмотрены два возможных решения (блоки 5.1., 5.2):
приведение параметров кривой усталости, в частности, амплитуды предела выносливости с использованием среднего значения нагрузочного режима S или коэффициента асимметрии r;
определение эквивалентной амплитуды для каждого цикла нагружения, приведенного к симметричному, при схематизации в виде двумерного распределения.
Следует иметь ввиду, что приведение нагрузочного режима к процессу о постоянным коэффициентом асимметрии не менее трудоемко" чем использование в расчетах двумерных распределений и поверхностей усталости.
Таким образом" в блоке 6 могут быть выполнены три независимых (параллельных) расчета: по "двумерной" гипотезе, с приведением параметров кривой усталости (блок 5,1); с приведением нагрузочного режима (блок 5.2), Каждый из них не исключает проведение расчетов по различным вариантам гипотезы при различных способах одномерной схематизации нагрузочного режима.
Окончательная оценка ресурса зависит от того, какими статистическими характеристиками представлены параметры кривой усталости N (S) и нагрузочного режима f (S), входящие в формулу (1.13). Если известны средние значения и дисперсии, то использование метода линеаризации (блок 6Л) позволяет определить оценки среднего и дисперсии ресурса по формулам
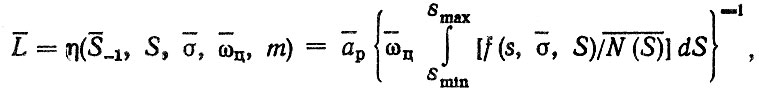 (2.29)
(2.29)где bi - i-й случайный параметр нагрузочного режима f (S, a, S) или кривой усталости N (S); ∂η/∂bi - частная производная по bi, определяемая при средних значениях bi; rij - коэффициент корреляции между параметрами bi, bj.
В случае не коррелированных параметров rij = 0 и формула (2.30) записывается в виде
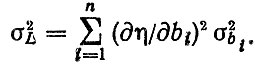 (2.31)
(2.31)
Рассмотрим пример, когда обобщенный нагрузочный режим подчиняется нормальному закону, а кривая усталости описывается степенной зависимостью (2.27). Допустим, что четыре параметра являются случайными и известны их средние значения и дисперсии: предел выносливости (S-1, σ2S-1) число циклов на 1 км пути (ωц, σ2ω), среднее значение нагрузочного режима (S, σ2S), дисперсия нагрузочного режима Воспользовавшись
формулами (2.29), (2.31), находим
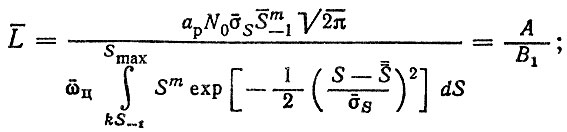 (2.32)
(2.32)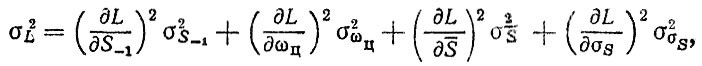 (2.33)
(2.33) где
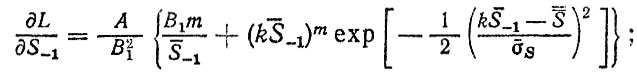
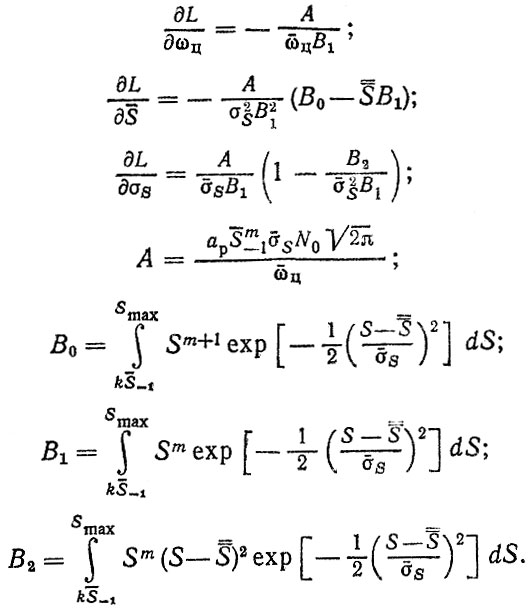
В частном случае при наличии средних значений параметров нагрузочного режима и кривой усталости можно получить только среднее значение ресурса. При известных законах распределения указанных параметров применение метода статистических испытаний позволяет получить функцию распределения ресурса, с помощью которой находятся средний, гамма-процентный ресурсы и др.
Выбор варианта существенно зависит от стадии разработки конструкции. Очевидно на ранних стадиях оценка параметров нагрузочного режима и кривой усталости может быть произведена на основании анализа аналогичных конструкций, главным образом, с использованием корреляционных зависимостей. По мере поступления информации о стендовых испытаниях, экспериментальных исследованиях нагрузочных режимов (блок 7) производится уточнение исходных данных (блок 8) и, следовательно, должна повышаться достоверность оценок долговечности.
Многовариантность расчетов, представленная в блок-схеме, объясняется стремлением исследователей и конструкторов повысить точность и гарантировать достоверность оценок ресурса. Здесь возможны следующие направления: уточнение корректирующих зависимостей и отдельных составляющих, входящих в формулу (1.13); установление взаимосвязей между отдельными блоками при определении основных составляющих, и использование их в окончательном варианте расчета; упрощение блок- схемы за счет использования интегральных характеристик. Поскольку окончательных рекомендаций по использованию того или иного варианта расчета не имеется, для оценки долговечности необходимо проводить расчеты по нескольким вариантам. За расчетный вариант (блок 9) принимается тот, при котором наблюдается наилучшее совпадение с результатами стендовых и эксплуатационных испытаний.
На основании блок-схема были проведены расчеты средних ресурсов различных деталей автомобилей для трех вариантов гипотезы суммирования повреждений. В расчетах были использованы обобщенные нагрузочные режимы, полученные экспериментально при режимометрических и тензометрических испытаниях.
Схематизация нагрузочных режимов производилась в соответствии с видом расчета, например для шестерен и подшипников в виде ординат крутящего момента, для полуосей - по максимумам, для накладок сцепления - в виде удельной работы буксования.
Переход от нагрузок к напряжениям при расчете зубьев шестерен на изгиб и контактную прочность выполнен в соответствии с рекомендациями работы [711, при расчете подшипников - в соответствии с работой [29], Параметры кривых усталости были выбраны на основе данных опубликованных в работах [7, 56]. Расчеты выполнены на ЭВМ по специально разработанным про-граммам.
На рис. 2.5 представлены результаты расчетов и фактические ресурсы деталей, определенные в процессе наблюдений за под-контрольными партиями автомобилей. Для некоторых деталей приведены прогнозируемые значения ресурса, полученные при обработке материалов незавершенных испытаний методом Джонсона.
Сопоставление расчетных (Lp) и фактических () ресурсов позволяет сделать следующие выводы.
Во-первых, расчетные значения ресурсов по первому и третьему вариантам гипотезы суммирования повреждений в большинстве случаев дают верхнюю и нижнюю границы фактического среднего ресурса (рис. 2.5, а). В тех случаях, когда фактический ресурс находится вне указанных границ, он превосходит верхнюю границу и, следовательно, в эксплуатации окажется не меньше расчетного.?
Во-вторых, при величине корректирующего коэффициента aр > 0,45 расчет следует производить по первому варианту гипотезы; при ар < 0,4 лучшее совпадение с фактическими ресурсами наблюдается при расчете по третьему (или второму) варианту гипотезы (рис, 2.5, б).
В-третьих, для деталей, не имеющих точки перегиба на кривой усталости, или в случае, когда основной спектр их нагрузок расположен выше предела выносливости, расчет по второму варианту гипотезы можно не выполнять, так как его результаты совпадают с первым вариантом,
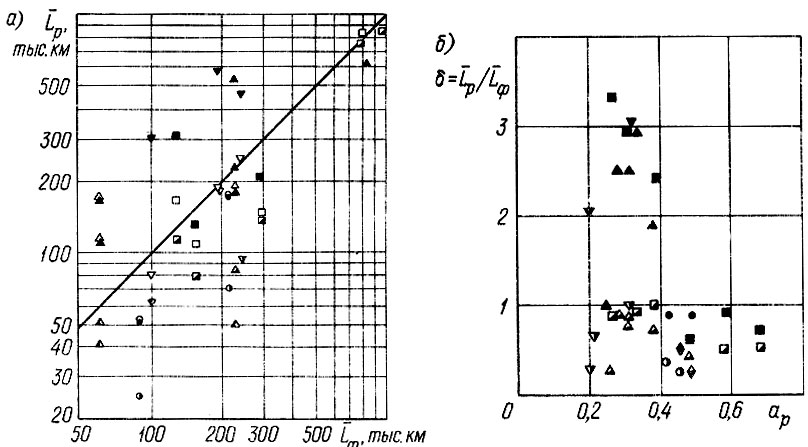
Рис. 2.5. Расчетные (Lp) и фактические (Lф) значения средних ресурсов: а - зависимость между Lp и Lф; б - зависимость между отношением Lр/Lф и корректирующим коэффициентом (закрашенные значки относятся к 1-му варианту гипотезы, светлые - ко 2-му и полузакрашенные - к 3-му варианту); ο - накладки сцепления; □ - шестерни; Δ - подшипники; ∇ - полуоси; ◊ - диски колес
Рассмотренная блок-схема может быть использована при разработке единого алгоритма расчета усталостной долговечности деталей автомобиля на ЭВМ.
Поскольку расчет по гипотезе суммирования повреждений основан на статистических и корреляционных зависимостях, то его результаты позволяют оценить ресурсы в среднем точно для всей совокупности рассчитываемых деталей. Для конкретной детали результаты расчета по первому и третьему вариантам гипотезы дают верхнюю и нижнюю границы фактического ресурса. Окончательная оценка ресурса производится по результатам стендовых, полигонных или эксплуатационных испытаний, но при этом число испытываемых элементов может быть значительно сокращено, а продолжительность испытаний и их стоимость существенно уменьшены.
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'