Глава 2. Методы расчета показателей долговечности и безотказности деталей автомобиля

2.1. Методы расчета на износ

В общем случае изнашивание является нестационарным случайным процессом обычно монотонно возрастающим. Известно, что нестационарность случайного процесса наблюдается по математическому ожиданию М (t), дисперсии D (t) и частоте (рис. 2.1). При описании реализаций износа применяются нестационарные процессы со "слабым" перемешиванием или процессы с последействием [12], у которых корреляционная (автокорреляционная) функция К_s(τ)≈1 (рис, 2.1, а, б). Это означает, что на анализируемом участке реализация износа может быть аппроксимирована апериодической функцией. Если K_s(τ)<<1 или содержит периодические составляющие, то такой процесс можно отнести к процессам с "сильным" перемешиванием (рис, 2.1, в, г).

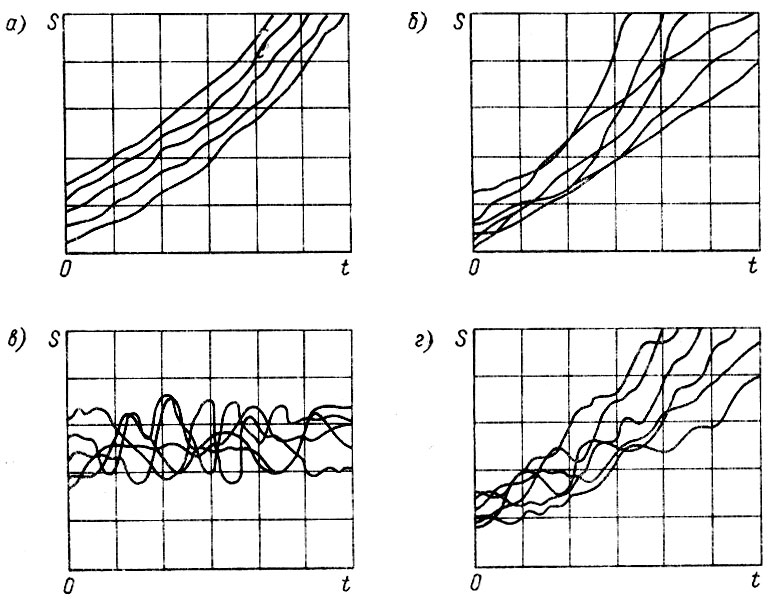
Рис. 2.1. Случайные процессы со 'слабым' (а, б) и 'сильным' (в, г) перемешиванием: а - процесс нестационарный по М (t); б - процесс нестационарный по М (t) и D (t); в - процесс стационарный по М (t) и D (f); г - процесс нестационарный по М (t) и D (t)

Нестационарные случайные процессы со слабым перемешиванием подразделяются на две группы. Первая группа - процессы нестационарные по математическому ожиданию М ((), называемые также "полуслучайными" (элементарными) [17], или фиксированная случайная величина

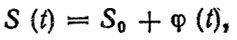(2.1)

где S (t) - реализация процесса; S₀ - случайная величина, описывающая реализации процесса в начальный момент времени; φ(t) - детерминированная монотонная функция времени.

Вторая группа - процессы нестационарные по М (t) и дисперсии D (t)

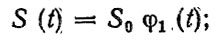(2.2)

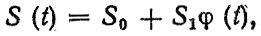(2.3)

где S₀, S₁ - случайные величины, как правило, независимые.

Частным случаем зависимости (2.3) является "веерная" функция вида

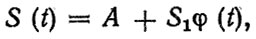(2.4)

где А - фиксированная величина.

Следует подчеркнуть, что к реализации процесса типа (2.4) при А = 0 сводится расчет по линейной гипотезе суммирования повреждения (см. п. 1.2), когда основная расчетная формула записывается в виде

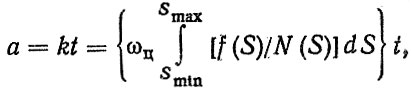(2.5)

где k - случайная величина; a - детерминированная или случайная величина.

При использовании в расчетах зависимостей (2.1)-(2.4) необходимо учитывать следующие особенности:

функции φ(f) и φ₁(t) должны удовлетворять условию φ(t) = 0 и φ₁(t) = 1 при t = 0, например φ(t) = αt^β, φ₁(t) = exp (kt);

если случайная величина S₀ в формуле (2.1) подчиняется таким законам распределения, как Вейбулла, Рэлея, гамма, логарифмически-нормальному, экспоненциальному без параметра сдвига, то функция распределения реализаций процесса F (S, t) для любого t > 0 будет описываться тем же законом, но с параметром сдвига ("порогом чувствительности" [12 ]) t₀ = φ(t). Аналогично для зависимостей (2.2)-(2.4) параметр сдвига может быть введен с помощью детерминированной функции фа (f) или непосредственно в (f):

если функции распределения F (S, f) для различных t подчиняются одному и тому же закону распределения, а параметры закона являются монотонными функциями от t, то для расчёта

плотности распределения ресурса f,(t) следует использовать формулу (1.12), которую можно записать в виде

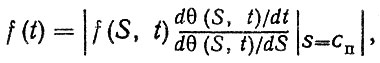(2.6)

где f(S, t) - плотность распределения функции F (S, t); θ(S, t) - последняя общая ступень дифференцирования по S и t, входящая в F (S, t); С_п - предельное значение (односторонняя граница) S (t);

если реализации износа описываются зависимостями (2.1), (2.2), (2.4), то для расчета f(t) вместо (2.6) можно воспользоваться формулой для закона распределения функции одного случайного аргумента

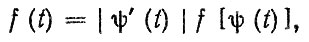(2.7)

где f[ ] - плотность распределения случайной величины S₀ или S₁; ψ(t) - зависимость для i, полученная из формул (2.1), (2.2), (2.4) при S = С_п.

Рассмотрим реализацию (2.1) в виде

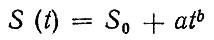(2.8)

при условии, что S₀ подчиняется распределению Вейбулла

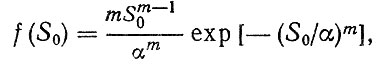
где a, m - параметры распределения.

При подстановке в (2.8) S (t) = С_п, где С_п - предельное значение износа, определим зависимости для ψ(t) и ψ'(t):

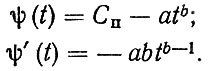
Если воспользоваться зависимостью (2,7), то плотность распределения ресурса

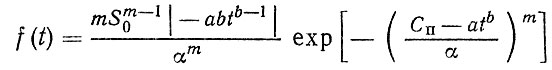(2.10)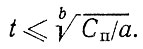

Формула позволяет получить несколько частных случаев для экспоненциального закона, m = 1; распределения Релея, m = 2; для линейных реализаций, b = 1.

Рассмотрим экспоненциальную зависимость

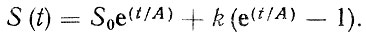(2.11)

Поскольку коэффициенты k и A являются детерминированными величинами, то данную зависимость можно отнести к реализациям вида (2.2), если ввести в нее детерминированную функцию типа φ(t), равную 0 при t = 0.

Процесс, описываемый реализациями (2.11), является нестационарным по математическому ожиданию и дисперсии, так как

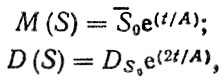
где S₀, D_S0 - математическое ожидание и дисперсия случайной величины S₀.

Для определения плотности распределения ресурса f(t) воспользуемся формулой (2.7), при условии, что S₀ подчиняется нормальному закону распределения

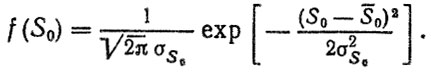(2.12)

Из (2.11) при S (t) = С_п находим

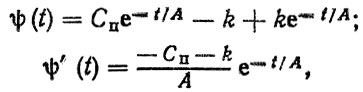
а выражение для плотности распределения ресурса запишется в виде

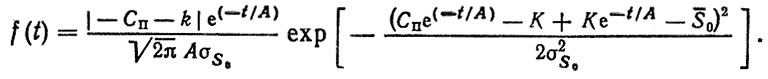(2.13)

При А = 1/b, k = 0 зависимость (2.13) соответствует плотности распределения ресурса для реализации износа S = S₀ exp bt [1].

Рассмотрим случайный процесс износа, каждая реализация которого описывается зависимостью (2.3) и определяется двумя случайными величинами S₀ и S₁. Если эти величины независимы, то при расчете плотности распределения ресурса f (t) можно придерживаться следующей последовательности.

1. Поскольку зависимость (2.3) является композицией законов распределения случайных величин, то для некоторых законов распределения (нормальных, гамма, Эрланга) удается получить f(S, t) аналитическим путем; дальнейший расчет производится по формуле (2.6).
2. Если композиция законов распределения не выражается в аналитическом виде, то вид плотности распределения f (S, f) находится с использованием диаграммы, приведенной на рис" 2.2. Для этого на основании теорем о числовых характеристиках случайных величин рассчитываются моменты для суммы независимых случайных величин S₀ и S_t:

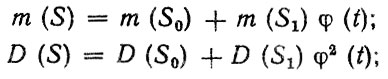
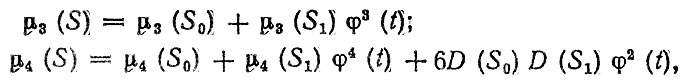(2.14)

где m (S) - начальный момент (математическое ожидание); D (S) - дисперсия (второй центральный момент); μ₃(S), μ₄(S) - соответственно третий и четвертый центральные моменты.

Осуществив переход к параметрам β₁ и β₀ по формулам

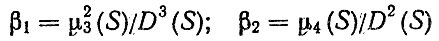(2.15)

по диаграмме определяется вид закона распределения f(S, t).

3. Для нахождения параметров распределения f(S, f) воспользуемся методом моментов [8]. Заметим, что согласно этому методу моменты распределения f(S, t), зависящие от неизвестных параметров, приравниваются эмпирическим моментам, определяемым в нашем случае по формулам (2.14).

Для примера рассмотрим случайный процесс износа, каждая реализация которого аппроксимируется степенной зависимостью

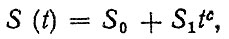<(2.16)br>

где c-неслучайная величина, c > 0.

Допустим, что величины 50 и подчиняются нормальным законам распределения с математическими ожиданиями m₀, m₁ и дисперсиями D₀, D₁. Известно, что для нормального закона третьи центральные моменты μ₃(S₀) = μ₃(S₁) = 0, четвертые центральные моменты μ₄(S₀) = 3D²₀, μ₄(S₁) = 3D²₁.

Найдем моменты распределения f (S|i)

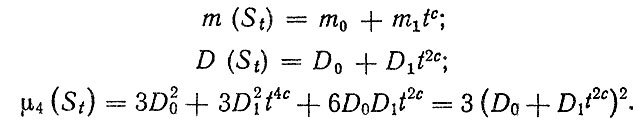
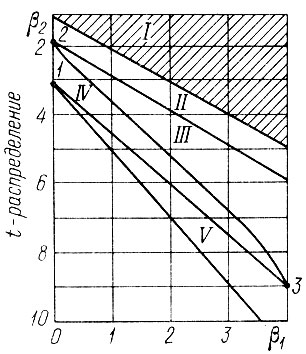
Рис, 2.2. Диаграмма для определения вида закона распределения случайной величины 1 - нормальный закон; 2 - равномерное распределение; 3 - экспоненциальное распределен βмне; I - критическая область; II - область U-образного β - распределения; III - область U-образного β-распределения; область β-распределения, γраспределения; V - область логарифмического нормального распределения

Определим параметры β₁, β₂ по формулам (2.15). Очевидно, что β₁ = 0, так как μ₃(S_t) = 0. При подстановке D(S_t) и μ₄(S_t) получим β₂ = 3. Тогда, из диаграммы (рис, 2.2) следует, что плотность распределения f (S, 0) подчиняется нормальному закону.

Очевидно, общая ступень дифференцирования для плотности нормального закона "распределения f (S, t)

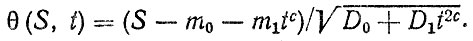
Выполнив преобразования согласно формуле (2.6), находим плотность распределения ресурса

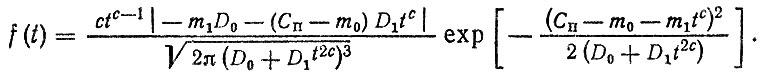(2.17)

Из формулы следуют частные случаи: α - распределение [при с = 1, D₀ = 0 формула (1.10)3; распределение Бернштейна [при с = 1 формула (1.11)]; распределение, приведенное в работе [463 при D₀ = 0, а также распределение, соответствующее реализации вида (2.1) при S₁ = 1, D₁ = 0 ("фиксированная" случайная величина).

В случае, если вместо реализации износа даны зависимости от времени для параметров распределения f(S|t), то расчет производится непосредственно по формуле (2.6). Так, для деталей двигателей [481 при среднем m(t) = a₁t + a₂t² + a₃t³ и среднем квадратическом отклонении σ(t) - b₀ + b₁t с учетом нормальности f (s) из (2.6) находим

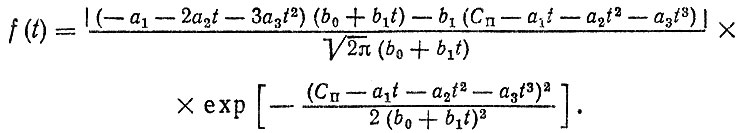
Второй вариант расчета основывается на применении для оценки среднего Т_ср и среднего квадратического значений ресурса σ_T метода линеаризации. Например, для часто используемой зависимости

(2.19)

где S₁ - случайная величина скорости изнашивания, при S = С_п

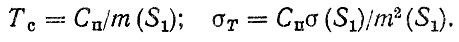(2.20)

В некоторых случаях можно использовать уточненные формулы [39]

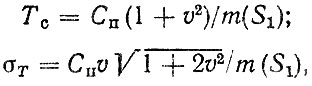(2.21)

где v = σ (S₁)/m (S₁) - коэффициент вариации.

Таким образом, для наиболее часто используемых экспериментальных зависимостей износа от времени удалось получить выражения для плотности распределения ресурса f (t). Однако применение полученных формул ограничено тем, что предельный износ С_п описывается постоянной величиной. Практический интерес представляет случай когда С_п является случайной величиной, подчиняющейся определенному закону распределения f(С_п). Тогда плотность распределения ресурса или его параметры находятся различными способами. Универсальным является способ" основанный на использовании методов статистического моделирования (метод Монте-Карло). При этом моделируются случайные величины начального износа с .плотностью распределения f (S₀), скорости изнашивания f (C_п) и случайные моменты концов реализаций, подчиняющиеся f (C_п).

Для нахождения моментов распределения f (t) можно воспользоваться, во-первых, методом линеаризации, во-вторых, формулами для среднего значения

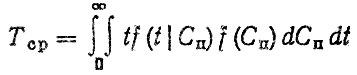(2.22)

i среднего квадратического отклонения

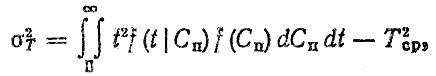(2.23)

где f (t|С_п) - плотность распределения ресурса, рассчитанная по формулам (2.6) или (2.7).

Рассмотрим пример расчета плотности распределения ресурса детали в случае, когда реализации износа подчиняются степенной зависимости (2.16) при с = 1,2, Допустим, что в момент t = 0, f (S, 0) подчиняется нормальному закону с параметрами S₀ = 80 мкм, σ_S0 = 20 мкм; случайные величины интенсивностей изнашивания S₁ - нормальному закону с параметрами S₁ = 1,1 мкм/тыс. км, σ_S1 = 0,3 . мкм/тыс. км;

распределение предельных значений износов - двухпараметрическому экспоненциальному закону

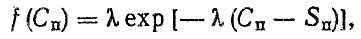(2.24)

где λ - параметр распределения, λ = 20 мкм^-1; S_п - параметр сдвига, S_п = 300 мкм.

При статистическом моделировании случайные величине наработок находятся по формуле

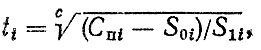
где С_пi, S_0i, S_1i - случайные величины, подчиняющиеся соответствующим законам распределения.

Смоделированные случайные величины наработок t_i подвергаются статистической обработке с целью определения f(t) и ее параметров.

При использовании метода линеаризации расчетные формулы для среднего значения и дисперсии записываются следующим образом:

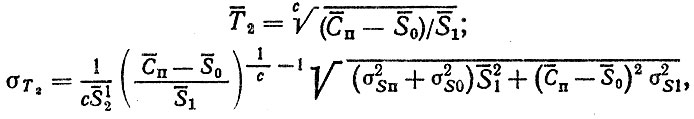
где C_п, σ_Sп - среднее значение и среднее квадратическое отклонение предельного износа.

Наконец, формула (2.22) расчета среднего значения f (t) для рассматриваемого примера записывается в виде

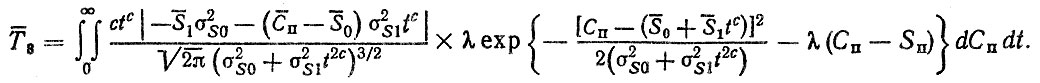
Аналогично σ²_T2 из формулы (2.23) определяется зависимость и для σ²_T3.

Выполненные расчеты показали, что

• при статистическом моделировании f(t) подчиняется трех параметрическому распределению Вейбулла с параметрами m = 1,55, T₀ = 403; порог чувствительности Т_с = 50 тыс. км; соответственно! среднее значение Т_c = 93,4 тыс. км, среднее квадратическое отклонение T₁ = 30,2 тыс. км (рис, 2.3);
• применение метода линеаризации позволило получить среднее значение Т₂ = 94,5 тыс, км? среднее квадратическое отклонение σ_Т2 = 26,2 тыс* км;
• при. расчете по формулам (2.22), (2,23) с использованием численного интегрирования среднее значение Т₃ = 99 тыс, км, среднее квадратическое отклонение σ_T3 = 27,1 тыс. км*

Таким образом, моменты распределения ресурса в данном примере практически совпадают, что говорит о возможности использования любого из трех рассмотренных способов.?