
Глава 5. Информационная база для прогнозирования надежности деталей и агрегатов автомобиля
5.1. Систематизация данных об условиях эксплуатации автомобилей
Для определения показателей надежности деталей по обобщенным нагрузочным режимам и корреляционным уравнениям долговечности необходимо располагать систематизированной информацией об условиях эксплуатации автомобилей. Анализ опубликованных данных [7, 54, 71] и накопленный опыт расчетов показал, что из большого числа показателей, используемых для описания условий эксплуатации, для агрегатов автомобиля целесообразно выделить ряд общих показателей, приведенных в табл. 5.1. Несомненно, при учете специфики расчетов конкретных деталей агрегатов могут потребоваться дополнительные данные, например темп включения сцепления и распределение частоты вращения двигателя для расчета работы буксования сцепления, распределение начальных и конечных скоростей автомобиля при торможении, распределение скоростей автомобиля при поворотах и т. д. Для характеристик дорог (помимо приведенных в табл. 5.1 коэффициентов и параметров микропрофиля) могут быть использованы параметры макропрофиля, число и распределение радиусов поворота, помехонасыщенность и т. д.
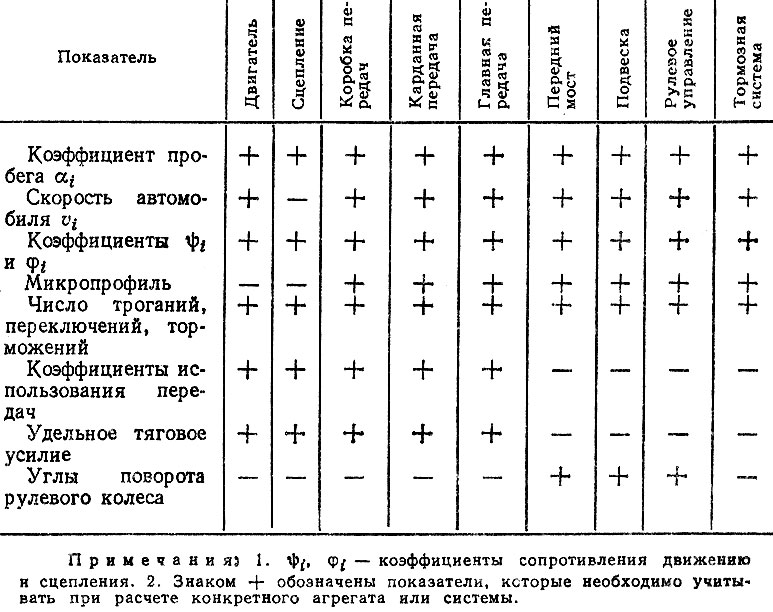
Таблица 5.1. Показатели условий эксплуатации (для расчета обобщенных нагрузочных режимов я КУД)
Рассмотрим некоторые из показателей.
Коэффициенты пробега по типам дорог αi. При построении КУД и расчете обобщенных нагрузочных режимов по данным подконтрольной эксплуатации αi определяются экспериментально. Для прогнозных расчетов показателей надежности на стадии проектирования они должны задаваться для соответствующих типов дорог* При отсутствии в техническом задании на проектируемый автомобиль коэффициенты αi могут быть приняты с учетом данных табл. 5.2 относящихся к 60-м годам и поэтому не отражающих в полной мере изменения дорожной сети в стране.
Для совершенствования расчетных методик оценки показателей надежности деталей автомобиля при проектировании следует разработать специальные нормативные материалы по выбору коэффициентов αi учитывающие тип автомобиля (самосвал, тягач и др.) и специфику перевозок (междугородние, сельскохозяйственные и т п.).
![Таблица 5.2. Распределение пробега автомобиля да дорогам различных категорий, %, [56, 58]](pic/000404.jpg)
Таблица 5.2. Распределение пробега автомобиля да дорогам различных категорий, %, [56, 58]
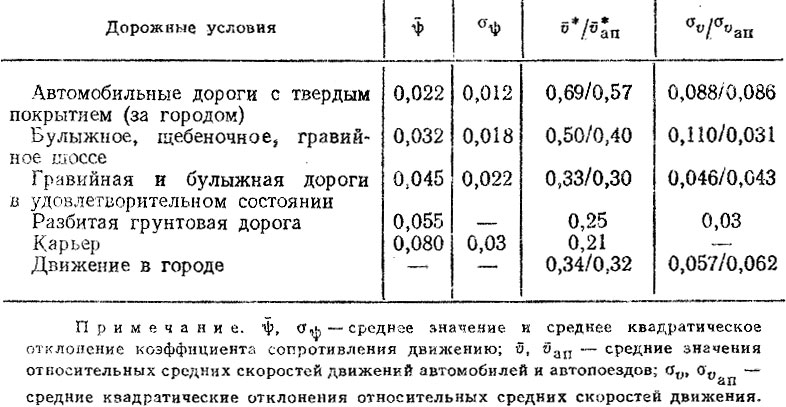
Таблица 5.3. Параметры распределения средних скоростей движения
Коэффициенты сопротивления движению ψi и скорости движения υi. В табл. 5.3 приведены параметры распределений коэффициентов ψi и относительных средних скоростей движения автомобилей в различных дорожных условиях. Параметры для ψi в основном взяты из работы [51]. Под 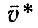 понимается отношение υ* = υ/υmax где υ, υmax - соответственно средняя в данных дорожных условиях и максимальная скорости автомобиля. Величины υ были взяты из работ [7, 19" 621, а также использованы данные режимометрических испытаний автомобилей, проведенных на кафедре "Автомобили и двигатели" ЛИСИ при участии авторов. Для относительных скоростей движения в зависимости от % были подобраны корреляционные уравнения (рис. 5.1) для грузовых автомобилей
понимается отношение υ* = υ/υmax где υ, υmax - соответственно средняя в данных дорожных условиях и максимальная скорости автомобиля. Величины υ были взяты из работ [7, 19" 621, а также использованы данные режимометрических испытаний автомобилей, проведенных на кафедре "Автомобили и двигатели" ЛИСИ при участии авторов. Для относительных скоростей движения в зависимости от % были подобраны корреляционные уравнения (рис. 5.1) для грузовых автомобилей
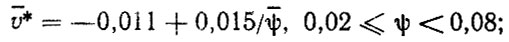 (5.1)
(5.1)для автопоездов (один прицеп или полуприцеп)
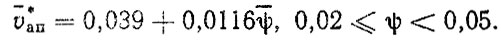 (5.2)
(5.2)
Разброс средних значений υ можно оценить с помощью средних квадратических отклонений συ. Так, при использовании правила "трех сигм" для грузового автомобиля на асфальтобетонных дорогах (за городом) при υmax = 90 км/час получим υ* =(-0,011 + 0,015/0,022) × υmax = 62 км/ч, συ = 0,088×90 = 8 км/ч; υ ± συ = 62 ± 24 км/ч.
Следует подчеркнуть, что мгновенные скорости движения одних и тех же моделей автомобилей в одинаковых дорожных условиях имеют значительный разброс и подчиняются различным законам распределения, в частности, нормальному, усеченному нормальному, логарифмически нормальному с параметром сдвига и др.
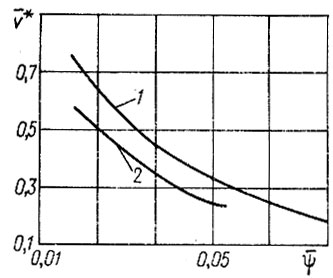
Рис. 5.1. Зависимости относительных средних скоростей движения автомобилей υ* от коэффициента сопротивления движению ψ: 1 - одиночные автомобили; 2 - автопоезда
Микропрофиль дороги. Ровность дороги определяется ее микропрофилем, одной из основных характеристик которого является спектральная плотность, описываемая, в частности, в виде полинома
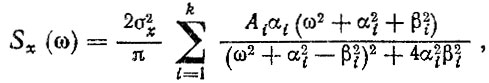 (5.3)
(5.3)где σx - среднее квадратическое отклонение ординат микропрофиля; αi, βi, Ai - коэффициенты,
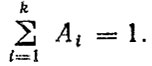
Обычно k ≤ 2, что вполне оправдано, так как с повышением точности описания микропрофиля конкретной дороги теряется общность выражения (5.3).
В табл. 5.4 и 5.5 приведены результаты статистической обработки микропрофиля автомобильных дорог. Из табл. 5.4 следует:
распределения средних квадратических отклонений ординат микропрофиля σx отличаются от нормального закона и подчиняются законам распределения с параметрами сдвига;
диапазоны значений σx соответствующих различным тинам дорог, пересекаются, поэтому, например, для конкретной грунтовой дороги σxi может оказаться меньше, чем для асфальтированной.
Коэффициенты пробега на передачах γik (по пути). Относительные пробеги на передачах yik были систематизированы так же, как и υ*, в зависимости от дорожных условий (табл, 5.6., 5.7). С увеличением коэффициента сопротивления движению наблюдается устойчивая тенденция изменения γik для отдельных передач. Так, при установке пяти ступенчатой коробки передач для низших передач (первая, вторая) с ростом ψ увеличиваются γi, для высшей передачи yt уменьшается, для третьей и четвертой передач зависимость γi от ψ носит параболический характер (рис. 5,2).
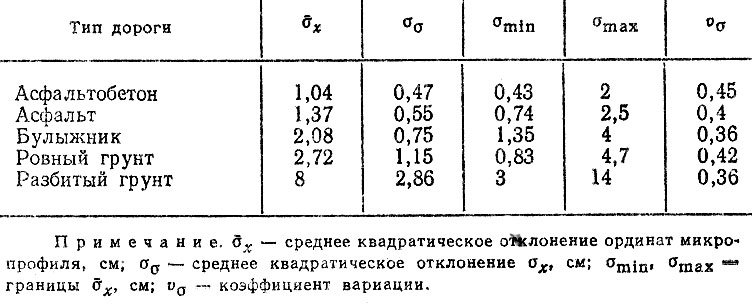
Таблица. 5.4. Осредненные параметры микропрофилей различных типов дорог
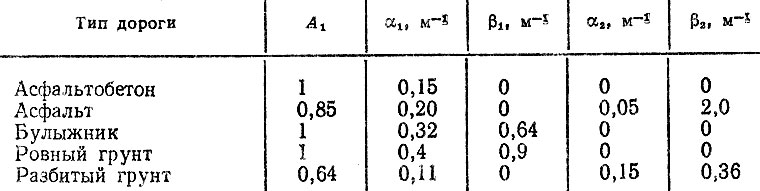
Таблица 5.5. Средние значения параметров нормированной спектральной плотности
Для сравнения в табл. 5.6 приведены данные о коэффициентах γi рекомендуемых для расчетов при проектировании зубчатых колес и подшипников коробок передач. Из нее видно, что коэффициенты γik, приведенные в [21, 74] для третьей - пятой передач, соответствуют движению в городе, а расчетные значения [711 для низших передач - гравийным и булыжным дорогам, для высших - условиям движения на автомобильных дорогах с твердым покрытием за городом.
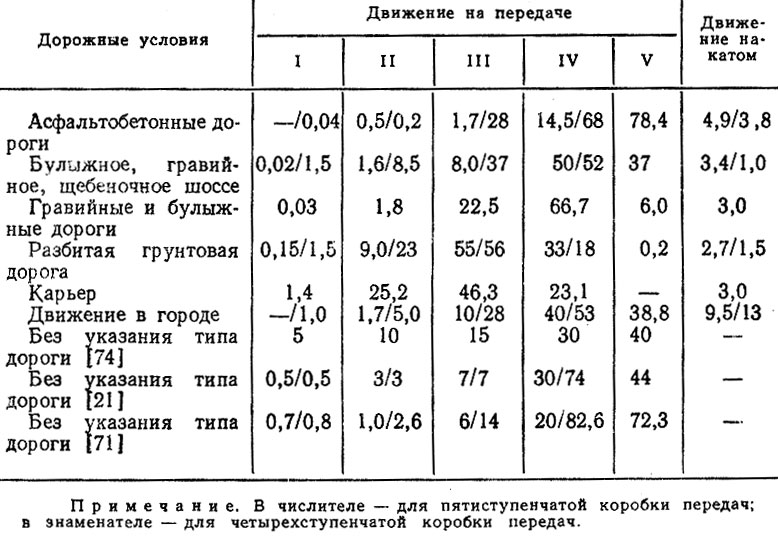
Таблица 5.6. Коэффициенты пробега грузовых автомобилей на передачах (по пути), %

Таблица 5.7. Корреляционные зависимости коэффициентов γik для различных коробок передач, %
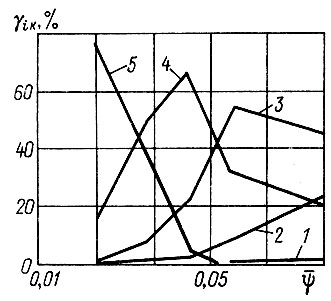
Рис. 5.2. Зависимость коэффициентов γik от коэффициента сопротивления движению φ (пяти ступенчатая коробка передач): 1-6 - номера передач
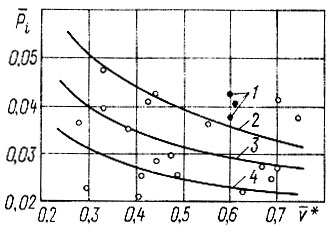
Рис. 5.3. Экспериментальные и расчетные значения средних удельных тяговых усилий: 1, 4 - по литературным данным; 2 - расчет по формуле (5.10); 3 - по осредненным экспериментальным данным, формула (5.6); ο - экспериментальные значения
Средние скорости движения на отдельных передачах зависят от ψ, υ* и распределения относительных пробегов γik. Для расчетов значения υik могут быть взяты из работ [7, 54] или рассчитаны по приближенной формуле
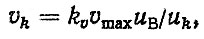 (5.4)
(5.4)
где υmax - максимальная скорость автомобиля; uk, uв- передаточные числа на k-и и высшей передаче; kv - коэффициент, kυ = 0,5 ÷ 0,75 (для расчетов принято kυ = 0,6).
Число троганий (nт) и переключений (nп) передач. В табл. 5,8 представлены данные о числе троганий и переключений передач за 1 км пробега. Эти показатели могут быть использованы для расчета неустановившихся режимов работы, в частности, при моделировании процессов движения с помощью колебательных систем, а также при определении максимальных нагрузок при расчетах на статическую прочность. Для элементов сцепления, синхронизаторов, а также приводов сцепления и коробки передач nт и пи используются для расчета КУД и нагрузочных режимов.
Удельные тяговые усилия. Вопросам исследования и расчета тяговых усилий на ведущих колесах автомобиля посвящено большое количество работ [19, 62, 69). На рис. 5.3 приведены некоторые экспериментальные данные в виде средних удельных тяговых усилий Pi для автомобилей общего назначения (главным образом с колесной формулой 4 X 2) в зависимости от υ* или ψ с учетом формулы (5.1). Величины Pi определялись по формуле
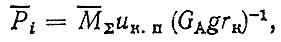 (5.5)
(5.5)где Pi - среднее удельное тяговое усилие на ведущих колесах в i-x дорожных условиях; МΣ - суммарный крутящий момент на полуосях, Н⋅м; uк. п - передаточное число колесной передачи; GA - масса автомобиля или автопоезда, кг; гΚ - радиус колеса, м; g ≈ 10 м⋅с-2.
Большой разброс экспериментальных данных объясняется отсутствием единой методики исследования нагрузочных режимов. Поэтому помимо объективных факторов существенное влияние на разброс данных оказали разные длины зафиксированных реализаций крутящих моментов; используемая аппаратура (от простейших режимометров до магнитной записи); различные способы схематизации, использованные при обработке.
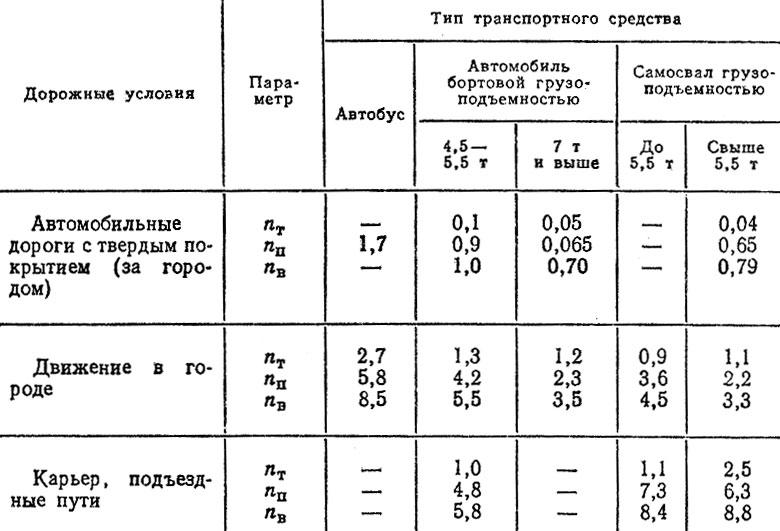
Таблица 5.8. Число троганий nт, переключений и общее число включений сцепления nв (за 1 км пробега)
Зависимость Pi от υ* может быть представлена в виде
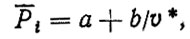 (5.6)
(5.6)где а = 0,016; b = 0,0072.
Аналитический метод расчета средних тяговых усилий, основанный на дифференциальном уравнении движения автомобиля, приведен в работах 129, 711. Расчет Рk производится по формуле
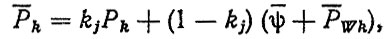 (5.7)
(5.7)
где Pk - среднее тяговое усилие на ведущих колесах на k-й передаче; kj - коэффициент инерционных нагрузок, для грузовых автомобилей kj = 0,3, для легковых и самосвалов - kj = = 0,2; PWk - среднее удельное сопротивление воздуха. Удельное тяговое усилие Рk определяется по формуле
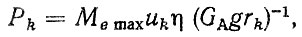 (5.8)
(5.8)где Memax - максимальный крутящий момент двигателя; uk - общее передаточное число трансмиссии при включении k-й передачи; η - КПД трансмиссии.
Величины ψ принимаются для грузовых автомобилей 0,03; для самосвалов - 0,05; PWk рассчитываются по известным формулам теории автомобиля,
В работе [19] приведена эмпирическая зависимость вида
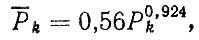 (5.9)
(5.9)
где Pk - определяется по формуле (5.8).
Для деталей трансмиссии, нагруженный на всех передачах, используется формула суперпозиции
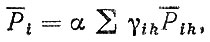 (5.10)
(5.10)
где α - коэффициент, α = 0,85÷0,95; γik - коэффициент пробега на передачах.
Например, по данным работы [71], для автомобиля FA3-53A расчетные значения коэффициентов γk и удельных тяговых усилий Pik на передачах составили: первой - γ1 = 0,008, Р1 = 0,126; второй - γ2 = 0,026, Р2 = 0,071; третьей - γ3 = 0,14, Р3 = 0,050; четвертой - γ4 = 0,826, Р4 = 0,038, Воспользовавшись формулой (5,10), при α = 1 найдем Pi = 0,008⋅0,126 + 0,026⋅0,071 + 0,14⋅0,05 + 0,826⋅0,038 = 0,041.
Расчетная средняя скорость υ = 51 км/ч, относительная средняя скорость υ* = υ/υmax = 0,61. Аналогичные расчеты показали, что для автомобиля ЭИЛ-130 Pi = 0,042 при υ* = 0,6; для автомобиля МАЗ-500А Рi = 0,037 при υ = 0,6. Из рис. 5.3 видно, что расчетные значения Рi находятся в верхней части корреляционного поля.
На рис. 5.3 также приведены результаты расчетов Рi для грузовых автомобилей по формулам (5.7) и (5.10) при α = 0,85 для различных дорог (кривая 2). Очевидно, эта зависимость характеризует верхнюю границу экспериментальных значений Рi. Нижней границей экспериментальных значений является кривая 4, построенная по данным [69] с учетом коэффициента γik (табл. 5.6) по формуле (5.10).
Формула (5.7) относится только к условиям движения автомобилей на дорогах с твердым покрытием за городом. В случае расчетов Pik для других типов дорог формулу (5.7) можно записать в виде
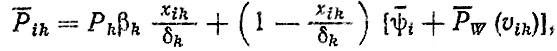 (5.11)
(5.11)где Pik - удельное тяговое усилие на k-й передаче в i-x дорожных условиях; βk - коэффициент использования загрузки двигателя (табл. 5.9); δk - коэффициент учета вращающихся масс; xik - коэффициент инерционных нагрузок (табл. 5.9).
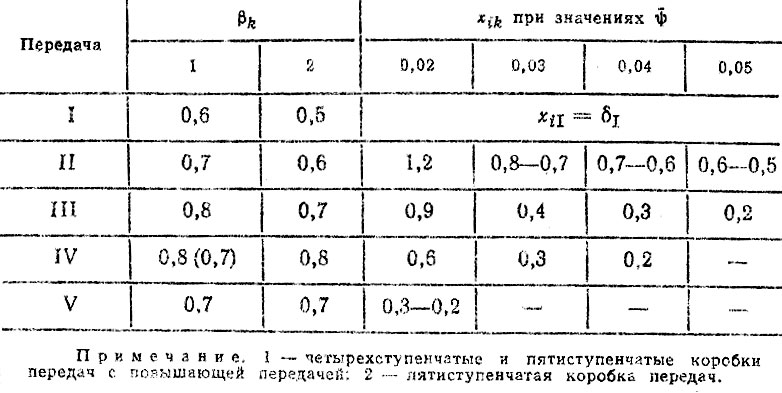
Таблица 5.9. Коэффициенты βk и xik для расчете удельных тяговых усилий
При использовании формулы (5.11) необходимо обратить внимание на следующее:
при средней скорости υ < 30 км/ч (дороги с ψ > 0,045) можно не учитывать составляющую от сопротивления воздуха Pw (υik) на всех передачах; при υ > 30 км/ч Pw (υik) учитывается только для высших передач;
для высших передач при xik/δk < 0,1 можно не учитывать инерционную составляющую во втором слагаемом, т. е. принять
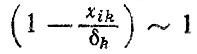
Для расчета средних квадратических отклонений σР проанализируем результаты работ [69, 71]. Согласно методике [29, 71], считается, что распределение удельных тяговых усилий на колесах при различных передачах подчиняется логарифмически-нормальному закону с параметрами: среднее значение а = lg Pk, среднее квадратическое отклонение σΛ = σlgP, где σlgP = 0,15÷0,20 для легковых автомобилей, σlgP = 0,20÷0,25 для грузовых автомобилей, σlgP = 0,20÷0,30 для самосвалов. Для деталей, нагруженных на всех передачах, величину σlgP принимают такой же, как и для отдельных передач.
Установим связь рекомендованных значений σΛ = σlg Р со средним квадратическим отклонением σPk. По формуле моментов
для среднего квадратического отклонения логарифмически нормального закона имеем
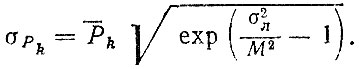
Подставляя значения σΛ = 0,2÷0,25, М = 0,4343, находим
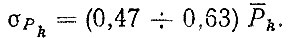 (5.12)
(5.12)Таким образом, с увеличением Pk пропорционально возрастает и σPk, В работе [19] предложена эмпирическая зависимость
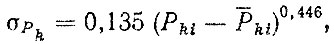 (5.13)
(5.13)где Pki - определяется по формуле (5.9).
Для удобства анализа примем показатель степени в формуле (5.9) равным 1, а в формуле (5.13) - 0,5. Тогда после упрощения
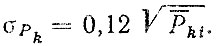 (5.14)
(5.14)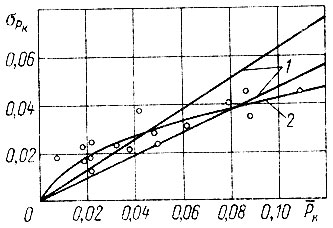
Рис. 5.4. Экспериментальные и расчетные значения средних квадратических отклонений σPk: 1 - по формуле (5.12); 2 - по формуле (5.14); О - экспериментальные значения
Соответственно выполнив переход к σΛ логарифмически нормального закона, можно записать
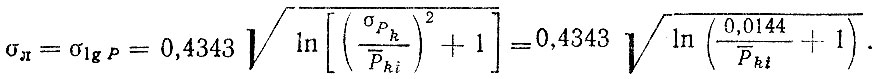 (5.15)
(5.15)
На рис. 5.4 приведены экспериментальные значения σPk и Рk [69] для четырех типов дорожных условий и различных передач; на этом же рисунке даны расчетные кривые для σPk [формулы (5.12) и (5.14)]. Из сравнения результатов видно, что зависимость (5.14) лучше описывает экспериментальные данные во всей области значений Pki и может быть использована для прогнозных расчетов σP (или σΛ).
На основании вышеизложенного можно сформулировать основные этапы определения показателей условий эксплуатации автомобилей на стадии проектирования.
- В зависимости от типа автомобиля выбираются коэффициенты пробега αi для дорог различных категорий (см. табл. 5.2).
- С помощью табл. 5,3 и формул (5.1), (5.2) определяются коэффициента сопротивления качению ψ(σψ) и параметры средних скоростей движения υi, συi (с учетом υmax)
- По табл. 5.4, 5.5 выбираются характеристики микропрофиля: σ2x, σσ и параметры нормированной спектральной плотности, используемые для расчета обобщенных нагрузочных режимов трансмиссии, ходовой части и др.
- В зависимости от типа коробки передач определяются коэффициенты пробега на передачах γik (см. табл. 5.6, 5.7); для коробок передач с делителями коэффициенты γik выбираются по данным, опубликованным в работах [54, 71].
- По данным [71 или по формуле (5.4) рассчитываются υik.
- Для i-го типа дороги и k-и передачи рассчитываются средние удельные тяговые усилия на колесах Pik по формуле (5.11); средние квадратические отклонения удельных тяговых усилий σPk для нормального закона рассчитываются по формуле (5.14), для логарифмически нормального закона σΛ - по формуле (5.15).
Для перехода от удельных тяговых усилий к крутящему моменту необходимо произвести преобразование случайной величины. Например, для полуоси автомобиля с колесной формулой 4×2 (без разнесенной главной передачи) при fik (Р), подчиняющейся логарифмически нормальному закону, имеем
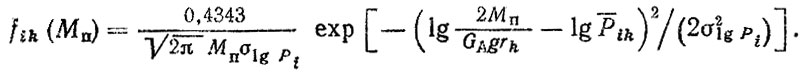
Для деталей, нагруженных на одной передаче, например шестерен коробки передач, формула (5.5) записывается в виде
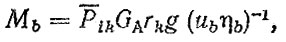
где Pik - удельное тяговое усилие на колесах; ub - передаточное число трансмиссии от рассматриваемой детали до ведущих колес; ηb - КПД соответствующего участка трансмиссии.
Так, для нормального закона (Р) находим
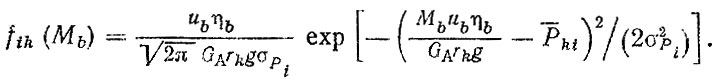
Для расчетов на статическую прочность и усталость помимо распределений удельных тяговых усилий определяются соответствующие характеристики амплитуд крутящего момента.
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'