6.4. Расчеты на долговечность деталей ходовой части

В работах [41, 80] показано, что для определения параметров нагрузочного режима элементов подвески и ходовой части можно воспользоваться методами статистической динамики. В общем случае расчет сводится к вычислению спектральных и взаимных спектральных плотностей процесса на выходе линейной или линеаризованной системы. При наличии одного входа в динамическую систему, эквивалентную подвеске автомобиля, можно записать

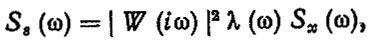(6.52)

где S_s (ω) - спектральная плотность на выходе, например, в виде динамического прогиба рессоры; W (iω) - передаточная функция системы; S_x (ω) - спектральная плотность на входе (ординаты микропрофиля дороги); λ(ω) - функция, характеризующая сглаживающую способность шин.

Для нормальных стационарных процессов с помощью S_s (ω) определяются следующие характеристики нагрузочного режима: среднее квадратическое отклонение плотности распределения

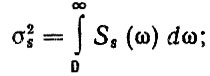
число пересечений среднего уровня на один километр пути

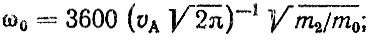(6.54)

число максимумов на один километр пути

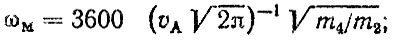(6.55)

критерий узкополосности процесса

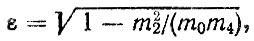(6.56)

где

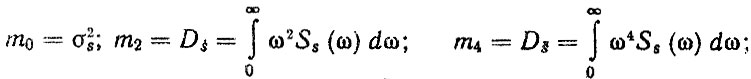
m₀, m₂, m₄ - моменты спектральной плотности" соответствующие самому процессу" его скорости s и ускорению s; υ_A - скорость автомобиля" км/ч.

Плотность распределения ординат процесса подчиняется нормальному закону, максимумов (минимумов) - распределению Райса, амплитуд - распределению Рэлея, двумерные распределения нагрузочного режима даны в п. 2.2

Для автомобилей с колесной формулой 4×2, 4×4 вертикальные колебания передней и задней подвески можно описать с помощью двух массовой колебательной системы; балансирную подвеску трехосных автомобилей - о помощью трех массовой колебательной системы.

Рессоры. Рассмотрим последовательность расчета на долговечность о использованием характеристик случайных процессов на примере листовых рессор. Поскольку преобладающим видом отказов рессор грузовых автомобилей являются усталостные поломки, то оценка ресурса должна производиться в соответствии с блок- схемой расчета на усталостную долговечность.

Входящие в формулу (6.52) передаточные функции для определения спектральной плотности S_h (ω) динамического прогиба рессор приведены в работах [41, 80]. Учитывая, что расчеты S_h (ω) производятся для заданной скорости автомобиля υ_A и загрузки Q, переход к обобщенному нагрузочному режиму осуществляется по формулам, приведенным в п, 5.3.

Для преобразования нагрузочного режима представленного в виде прогибов рессоры h, в напряжения S, возникающие в рессоры можно воспользоваться формулой

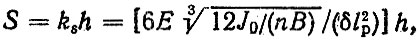(6.57)

где k_s - коэффициент преобразования; Е - модуль упругости, Е = 2,1⋅10⁶ МПа; J₀ - момент инерции центрального сечения рессоры; В, l_p - ширина листов и рабочая длина рессоры; n - число листов; δ - коэффициент деформации, δ = 1,25÷1,45.

Кривые усталости рессор определены в виде степенной зависимости (2.27); значения параметров m и N₀ даны в табл. 6.14.

По результатам испытаний образцов, отдельных листов и рессор в сборе получено выражение для амплитуд предела выносливости рессор

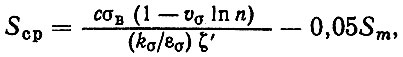(6.58)

где с - коэффициент, с = 0,4; σ_B - предел прочности материала рессоры; υ_σ - коэффициент вариации пределов выносливости отдельных листов, υσ = 0,04÷0,12; β - коэффициент упрочнения; k_σ/ε_σ - коэффициент, отражающий влияние контактных напряжений и коррозии трения [30], k_σ/ε_σ = 2,0; ζ' - поправочный коэффициент на предел прочности, ζ' = 2,0; S_m - среднее напряжение в рессоре (по статическому прогибу).

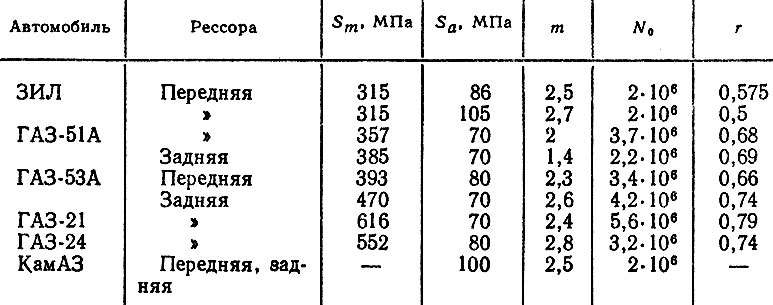
Таблица 6.14. Параметры кривых усталости рессор

Расчеты средних ресурсов трех вариантов ЛГСП были выполнены для 17 передних и 16 задних (основных) рессор для под-контрольных групп автомобилей ГАЗ, ЗИЛ, МАЗ, КрАЗ и др. Плотность распределения нагрузочного режима была представлена различными законами распределения: нормальным, Райса, Рэлея. Сопоставление расчетных с фактическими средними ресурсами рессор до первого отказа показало, что наиболее приемлемым является II вариант гипотезы при аппроксимации нагрузочного режима законами Райса и нормальным.

КУД листовых рессор. В результате поиска критериев долговечности наиболее удовлетворительной оказалась двумерная модель

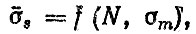
составляющие которой определяются по формулам,

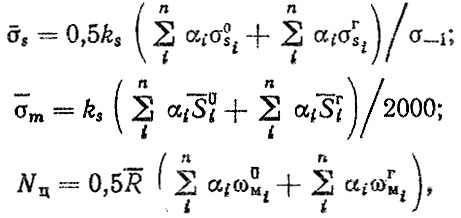
где σ⁰_si, σ^Γ_si - среднее квадратическое отклонение динамического прогиба рессоры при движении по дороге о i-м покрытием? S⁰_i, S^Γ_i - статический прогиб рессоры; ω⁰_Mi, ω^Γ_Mi - число максимумов, формула (8.52); k_s - коэффициент, формула (6.57) (индексом "0" помечены параметры, соответствующие режиму движения без груза, индексом "Γ" - с грузом).

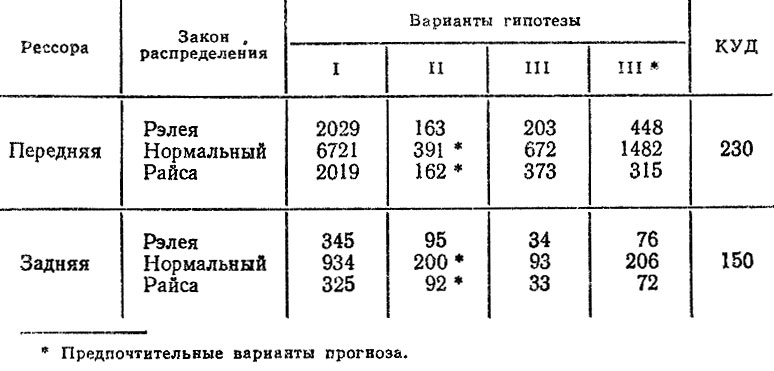
Таблица 6.15. Прогноз оценки средних ресурсов рессор автомобилей КамАЗ-5320, тыс. км

Для прогноза средних ресурсов с учетом временного тренда были получены соответствующие КУД

для передних рессор

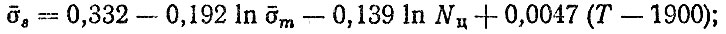
для задних рессор

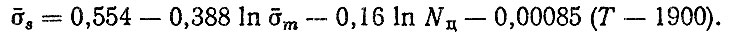
В табл. 6.15 приведены прогнозные оценки средних ресурсов передних и задних рессор (до первого отказа) по ЛГСП и КУД для подконтрольной группы автомобилей КамАЗ-5820. Допустим,

для комбинированного прогноза коэффициенты γ_i = 0,33. Тогда для предпочтительных вариантов по ЛГСП и КУД находим оценки прогнозных ресурсов: для передних рессор R_n = 261 тыс. км; для задних рессор R₃ = 147 тыс. км. Расчетные оценки косвенно подтверждаются результатами наблюдений: на пробегах до 150 тыс. км не отмечено отказов передних рессор; у задних рессор имелось значительное количество отказов, но они носили в основном прочностной характер и были связаны с неудовлетворительной конструкцией стремянок у первых партий автомобилей КамАЗ.

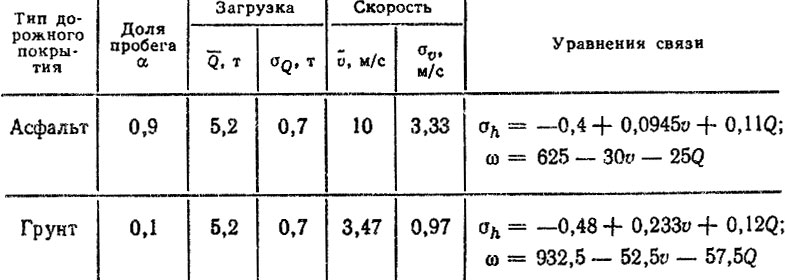
Таблица 6.16. Характеристики нагрузочного режима рессоры

При расчете ресурса рессор по гипотезе суммирования повреждений наиболее сложным является этап вычисления дисперсии или среднего квадратического отклонения σ_L. В работе [41] приведены примеры вычислений σ_L с использованием метода линеаризации по формуле (2.31) для независимых параметров. Рассмотрим пример вычисления σ_L с учетом корреляции между характеристиками обобщенного нагрузочного режима r_ij для частного случая (5.43), когда υ и Q независимы, нормально распределены и статистически связаны с параметрами нагрузочного режима линейными уравнениями (табл. 6.16). Полагая параметры кривой усталости независимыми и считая критерий узкополосности ε = const, получим следующую корреляционную матрицу

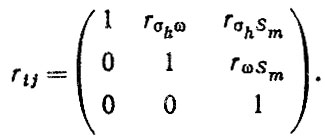(6.59)

Расчет элементов матрицы проиллюстрируем на примере вычисления r_σhω. Найдем функции, обратные (5,43), с учетом аппроксимирующих зависимостей из табл. 6.17. Для асфальтированной дороги имеем

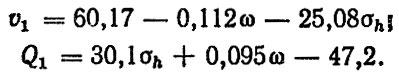
Вычислим якобиан преобразования

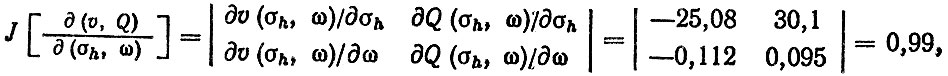
Совместная плотность распределения параметров нагрузочного режима с учетом независимости υ и Q и формул преобразования имеет вид

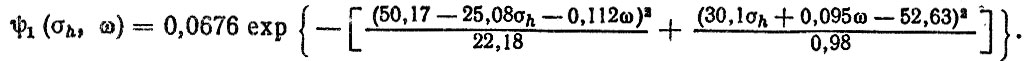
После аналогичных вычислений для грунтовой дороги получим

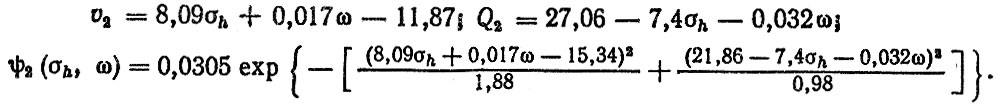
Применив формулу суперпозиции, найдем обобщенное распределение

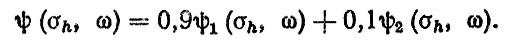(6.60)

Далее, вычисляя первый и второй моменты суперпозиции (6.60), с учетом (5.45) получим:_h = 1,11 см; σ_σh = 0,31 см; ω = 221 цикл/км; σ_ω = 125 цикл/км.

Коэффициент корреляции r_hω с учетом найденных значений параметров вычисляется по формуле

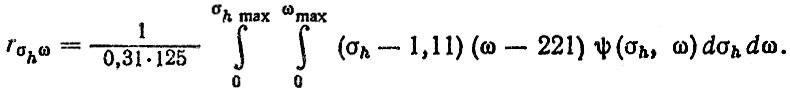(6.61)

Верхние пределы _{h max} и _max могут быть определены по правилу трех сигма или по формуле (5.33). После численного интегрирования выражения (6.61) при σ_{h max} = 2,1 см ω_max = 646 цикл/км получим r_hω = 0,577.

Тормоза. Одними из наименее надежных элементов тормозной системы являются фрикционные накладки. Характерная причина их отказа - износ вследствие истирания. Нагрузочный режим накладок определяется силовыми, скоростными и температурными воздействиями. Наиболее распространенным показателем их нагруженности, применяемым в расчетах, является работа трения.

Для расчета тормозных накладок на долговечность можно применить три метода: по гипотезе суммирования повреждений, на износ по предельному состоянию и по корреляционным уравнениям долговечности по аналогии о накладками сцеплений [41].

Рассмотрим пример расчета на износ по предельному состоянию. Положим, что при общей толщине накладки И предельно допустимая их толщина, исходя из технических условий, составляет h'. Тогда предельно допустимый износ будет h = H - h'. При постоянной интенсивности износа 8 средняя долговечность находится по формуле L = h/δ. Если 6 является величиной случайной, не зависящей от пробега и имеет плотность распределения φ(δ), что соответствует реальным условиям эксплуатации автомобилей, то плотность распределения ресурса накладок f(L) можно найти по формуле (2.7):

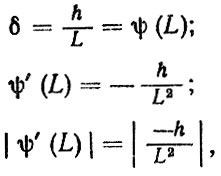
следовательно,

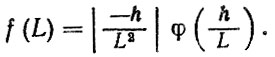(6.62)

Положим, что φ(δ) подчиняется распределению Вейбулла с параметрами а и (5:

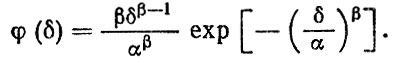
Для условий неинтенсивного магистрального движения по асфальтированным и грунтовым дорогам автомобилей средней грузоподъемности с полной нагрузкой можно принять α = 0,7712 и Р = 1,442. Подставив численные значения параметров в (6.82), получим

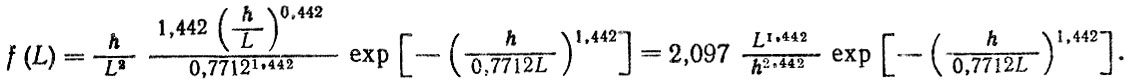
При h = 10 мм средний ресурс накладок L = 34 тыс. км.

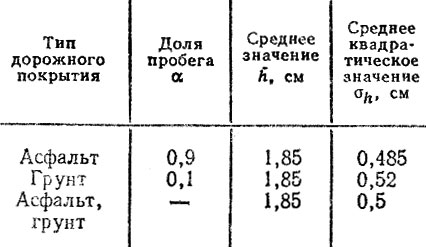
Таблица 6.17. Нагрузочный режим шин переднею колеса

Диски колес. В расчетах дисков колес на долговечность в первом приближении можно ограничиться рассмотрением только длительно действующих изгибающих моментов от вертикальных нагрузок. Правомерность такого упрощения обусловлена относительной кратковременностью действия боковых сил" возникающих при криволинейном движении автомобиля.

Рассмотрим пример расчета на долговечность дисков передних колес автомобиля грузоподъемностью 4,5 т, устанавливаемых с ободьями типа 7-20, для указанных в табл. 6.17 условий эксплуатации. Кривую усталости этих дисков представим в виде

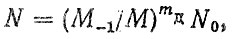(6.63)

где М_-1 = 0,53 кН⋅м, m_д = 4,1, N₀ = 6,8⋅10¹⁰ циклов.

Нагрузочный режим определим расчетным путем, воспользовавшись соотношением (6.52) и системой уравнений, описывающих вертикальные колебания автомобиля. Нормальная сила, действующая на обод колеса, определяется вертикальной реакцией дороги и, следовательно, ее микропрофилем. Результаты расчетов динамического прогиба шины h по формулам (6.52-6.56) представлены в табл. 6.17. Параметры колебательной системы и дорожного микропрофиля, а также последовательность вычислений подробно представлены в работе [41 ]. Обобщенное распределение прогибов шины приближенно можно описать нормальным законом с параметрами h = 1,85 см и σ_h = 0,5 см. Для определения нормальной нагрузки от дороги на одно колесо воспользуемся преобразованием R = С_Шh/2, где С_ш - жесткость шин одного моста (С_ш = 1300 даН/м), Получим нормальное распределение величины R (кН)

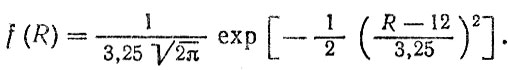(6.64)

Выполнив еще одно преобразовение М = lR, где l = 0,16 м - вылет диска колеса указанного автомобиля, найдем распределение изгибающего момента М (кНм)

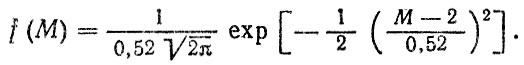
Найдя по формуле (5.33) М_max = 4 кНм и полагая М_min = 0, ω = 325 цикл/км, что соответствует одному циклу приложения пульсирующей нагрузки за один оборот колеса, с учетом (6.63) но формуле для общего случая ЛГСП (1,13) получим: по первому и второму вариантам гипотезы L_I,II = 612 тыс. км; по третьему варианту L_III = 282 тыс. км. Снижение предела выносливости до M_min = 0,6M_-1 в данном случае не повлияло на расчетную долговечность.

Таблица 6.18. Параметры подшипников управляемых колес

Подшипники ступиц. Рассмотрим пример определения долговечности подшипников ступицы управляемых колес автомобиля грузоподъемностью 4,5 т. Для этого воспользуемся результатами расчета нормальной нагрузки R на переднее колесо т. е. зависимостью (6,64) 1 при той же интенсивности нагружения ω = 325 цикл/км. Приведенную нагрузку на подшипники Р определим согласно методике, изложенной в работе [41], Параметры конических роликовых подшипников, установленных в опоры по схеме "0", приведены в табл. 6.18.

Расстояние между точками приложения реакций и торцами наружных колец подшипников найдем по формуле

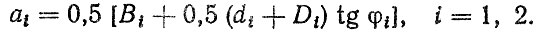
Имеем

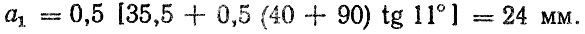
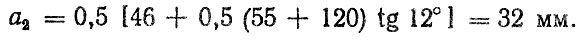
С учетом полученных значений а₁ и а₂ расстояние между точками приложения реакций

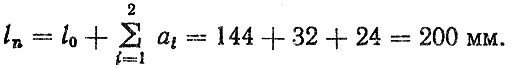
Найдем расстояние от точек приложения реакций до плоскости действия вертикальной нагрузки

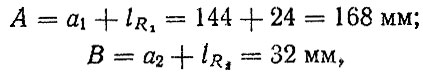
и определим радиальные нагрузки на опоры (кН)

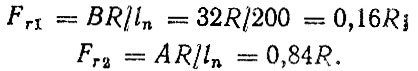
Вычислим осевые составляющие через радиальные. Для роликовых подшипников F_ai = и_ie_iF_ri, где b_i = 0,83 e_i = 1,5tg φ_i. Следовательно,F_a1 = 0,83⋅1,5 tg (11°)⋅0,16⋅R = 0,029R и F_a2 = 0,223R.

Исходя из условий нагружения F_a1 < F_a2 принимаем F_a1 = F_a2 =0,223R. Для подшипников ступиц коэффициент безопасности можно принять равным k_σ = 1,75, а коэффициент вращения k_υ = 1,2, так как вращающимся является наружное кольцо. Коэффициенты k_T и k_M принимаем равными 1. Для определения коэффициентов k_Fr и k_Fa вычислим отношения k_ei = F_ai/(k_υF_ri). Получим k_e1 = 1,16 и k_e2 = 0,221. Поскольку k_e1 > e₁, то имеем для первой опоры k_Fr1 = 0,4 и k_Fa1 = 0,4 ctg φ = 2,06. Для второй опоры k_e1 < е₂ и, следовательно, k_Fr2 = 1, k_Fa1 = 0. Подставив значения коэффициентов в формулу для приведенной нагрузки (6.42), получим:

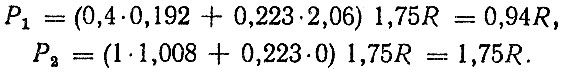
Выполнив преобразование зависимости (6.64) с учетом полученных выражений для приведенной нагрузки Р₁ будем иметь: для первой опоры

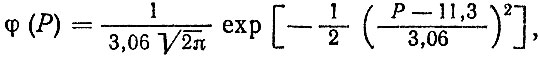
для второй опоры

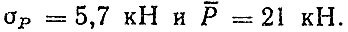
Подшипники относятся к деталям, требующим повышенной надежности, поэтому их долговечность будем определять исходя из условия не разрушения 90% (γ =90%). Кривая усталости в этом случае представляется в виде

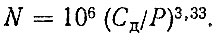
Для подшипника первой опоры с учетом (6.40) получим

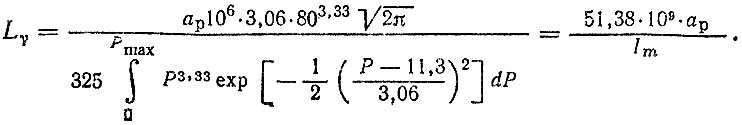
Значение Р_max, найденное по формуле (5.33), равно 23 кН, После численных расчетов получим I_m = 31,7⋅10³, a_p = 0,49, Следовательно, по первому и второму вариантам гипотезы имеем L_I,II = 1620 тыс. км, по третьему варианту - L_III = 794 тыс. км.

Выполнив аналогичные вычисления для подшипника второй опоры, найдем L_I,II = 1600 тыс. км и L_III = 800 тыс. км. Расчетные значения ресурсов получились завышенными по сравнению с фактическими. Это объясняется прежде всего тем, что в расчете не учтены нагрузки от осевой силы и изгибающего момента, возникающих при криволинейном движении автомобиля, а также нагрузки от продольной составляющей, появляющейся при торможении. Кроме того, на долговечность подшипников ступицы существенное влияние оказывает усилие затяжки, которое помимо осевой нагрузки вызывает резкое изменение температурного режима работы узла.

Отметим, что при сопоставлении расчетных и фактических долговечностей необходимо учитывать количество однотипных подшипников в конструкции и, если данные наблюдений обезличены (в выборках объединены отказы подшипников правых и левых колес), то следует применять при расчете распределение минимальных членов.

Шины. Наблюдения за автомобильными шинами в эксплуатационных условиях показывают, что основными причинами выхода их из строя являются: износ протектора (до 50% случаев), усталостное разрушение боковин и корда (10-15%), прочностные разрушения (порезы, проколы и т. д.). Поэтому ресурс шин должен определяться как по частным моделям (износ, усталость, прочность), так и по общей модели, учитывающей все три вида разрушения.

Рассмотрим расчет шин на износ для принятых в табл. 6.18 условий. Эти условия практически совпадают с режимом обычных полигонных испытаний грузовых автомобилей и прицепов. Интенсивность износа протектора шин и автомобилей данного класса, определенная для указанных условий на испытательном пробеге до 25 тыс. км, может быть представлена нормальным распределением с параметрами u = 0,448 и σ_u = 0,134, имеющими размерность мм/тыс. км. Полагая параметры u и σ_u независящими от пробега автомобиля и используя преобразование (2.7) при L = h/u, где h - предельно допустимый износ протектора (h = = 18 мм), получим распределение ресурса шин по износу

Если предположить, что распределение f_u (L) близко к нормальному в реальном эксплуатационном диапазоне пробега L, то среднее и среднее квадратическое значения ресурса можно вычислить по приближенным формулам

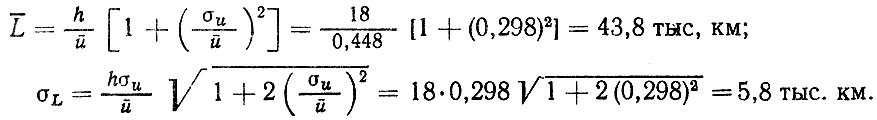
Численное решение по формулам для математического ожидания и среднего квадратического отклонения (при 0 < L < 15 тыс. км) дает L = 45 тыс. км σ_L = 9,2 тыс. км.

Найдем вероятность выхода из строя шин по износу протектора на установленном испытательном пробеге L_y = 25 тыс. км.

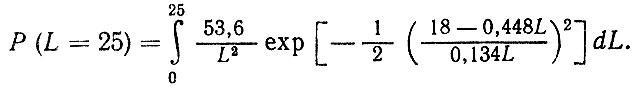
Численное решение интеграла дает Р (L = 25) = 0,012, Иными словами, на установленном пробеге в указанных условиях лишь одна из ста испытываемых шин может иметь полностью изношенный протектор.

Для расчета корда и боковин шин на усталость по гипотезе суммирования повреждений воспользуемся результатами расчета их динамической нагруженности от дороги (табл. 6.18). Кривую усталости можно представить в виде (по данным M. И. Рекитара)

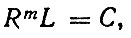
где R, L - нагрузка на шину (кН) и ее наработка до разрушения (в тыс. км) соответственно; m, С - константы. Для шин рассматриваемого типа можно принять: m = 4,6; С = 0,757⋅10⁸. С учетом нормального распределения нагрузки R (6.64) получим

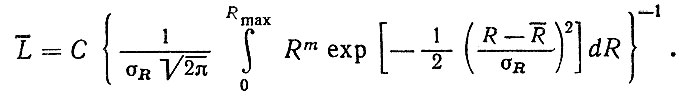
Подставив значения параметров и выполнив численное интегрирование, найдем

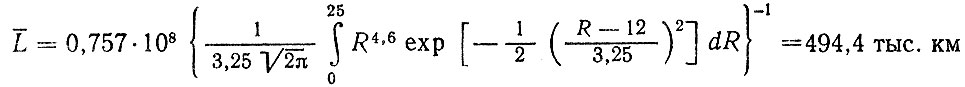
Для вычисления дисперсии рассеяния ресурса по усталости можно воспользоваться формулами линеаризации (2.30) или смоделировать случайные наработки шин методом Монте-Карло, полагая параметры R, σ_R, m, и С случайными. Последний вариант дает возможность получить не только среднее и среднее квадратическое значения ресурса шин по усталости, но и оценить плотность распределения f_y (L).

Расчет на прочность выполняется с использованием модели "нагрузка - несущая способность" по формуле (1.17) при известном распределении прочностных свойств основы шины. Общая расчетная модель, учитывающая все три вида разрушения, соответствует модели "слабейшего звена" (табл. 2.2). Оценки ресурса шин с учетом всех трех видов разрушений, учитывая различный вид распределений f_j (L), j = 1, 2, 3, целесообразно определять на ЭВМ методом статистических испытаний.

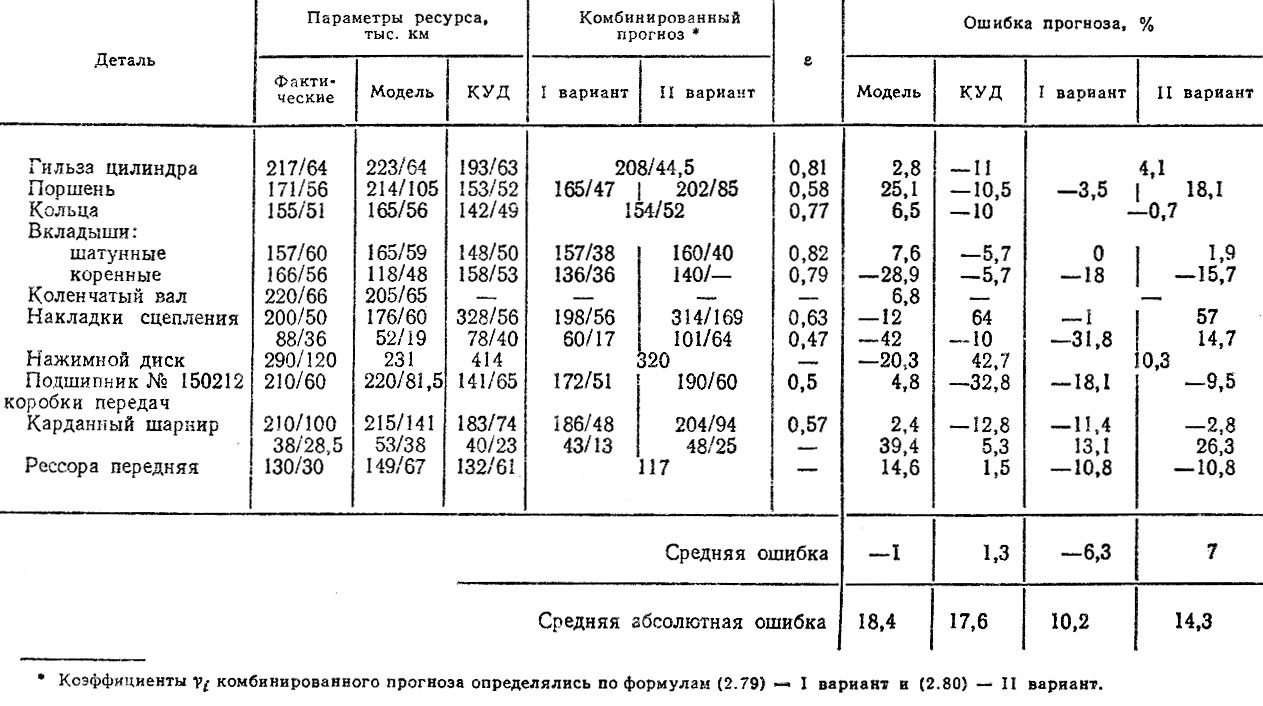
Таблица 6.19. Результаты прогнозирования ресурса деталей автомобиля

В заключение отметим, что повышение достоверности прогнозных оценок ресурсов деталей и агрегатов автомобилей неразрывно связано с экспериментальными исследованиями их надежности в различных условиях эксплуатации, в том числе и реальных. Повышение точности расчетов и дальнейшее развитие методик может быть осуществлено не только путем совершенствования алгоритмов, корректирования моделей отказов, но, главным об разом, в результате сопоставления прогнозных и фактических данных о надежности. Точность прогнозирования ресурсов деталей по изложенным методикам можно оценить по табл. 6.19, в которой приведены расчетные и фактические данные по параметрам ресурсов и ошибки прогнозирования по разным вариантам. Из табл. 6,19 следует, что средние ошибки комбинированного прогноза по рассмотренной группе деталей составляют ±7%, а абсолютные средние ошибки не превышают 15%. Можно заметить, что повышение меры непротиворечивости ведет к уменьшению ошибок прогноза. Комбинированные методы позволяют получить более точные оценки средних ресурсов по сравнению с другими алгоритмами. В интервале ±20% от фактических значений ресурса находится до 90% оценок комбинированного метода, в то время как для КУД эта величина составляет 75%, а для моделей отказов - до 40%.