
6.3. Расчет показателей надежности агрегатов
В большинстве случаев наиболее эффективным путем решения задач определения показателей надежности агрегатов является моделирование на ЭВМ с применением метода статистических испытаний (Монте-Карло). Многократное проигрывание моделей дает случайные последовательности наработок, которые обрабатываются затем обычными статистическими методами.
На рис. 6.4 представлен один из вариантов схемы моделирования ресурса R составляющих агрегат деталей до первого отказа. Отработка алгоритма осуществляется следующим образом. С по-мощью генератора случайных чисел (ГСЧ) моделируется вектор случайных чисел (СЧ) размерностью N, Поскольку модель
долговечности обычно включает независимые и зависимые случайные величины (СВ), то вектор делится на два вектора размерностью тир для моделирования m одномерных и р многомерных СВ. Результатом моделирования является вектор {ζj}N случайных аргументов модели долговечности L I-й детали {Zj}N системы. Помимо вектора {Zj}N модель долговечности включает также вектор неслучайных аргументов {Sl}A. Повторяя расчет Т раз, получим случайную последовательность наработок {Lr}T.
Расчет выполняется для R элементов агрегата, причем для каждой l-й детали задается своя модель долговечности ψl [{Zj}N,{Si}A] и свои распределения случайных аргументов вектора {Zj}N. Результатом расчета и обработки являются функционалы G и F, определяющие плотность распределения ресурса φl(L) и вероятность безотказной работы Рl (L) составляющих агрегат R элементов
При моделировании показателей надежности восстанавливаемых систем последующие отказы находятся по рекуррентной формуле
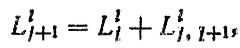 (6.48)
(6.48)где Llj,j+1 - наработка 1-й детали между j и j + 1 отказами. Для моделирования наработок между отказами можно воспользоваться корреляционными зависимостями или ввести функции "старения", которые обычно задаются в виде весовых коэффициентов αll к наработкам до первого отказа
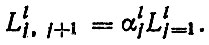
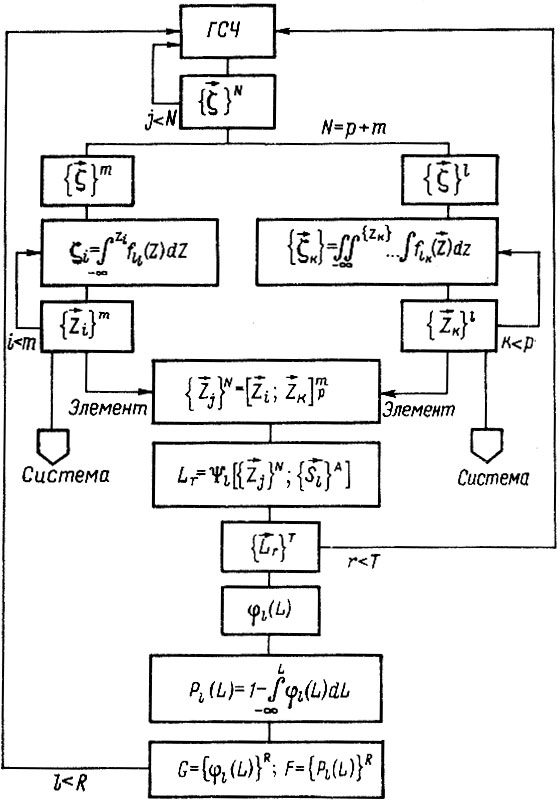
Рис. 6.4. Схема моделирования ресурса R деталей системы до первого отказа
В результате моделирования n реализаций первых и последующих отказов l-й детали рассматриваемой системы (агрегата) получим матрицу наработок
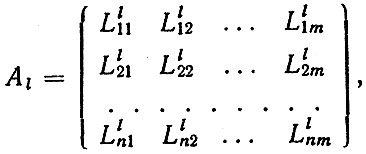 (6.49)
(6.49)где Lijl - i-я реализация наработки l-й детали до j-го отказа; m - число отказов.
Выполнив расчеты наработок для всех деталей и представив их в виде матриц (6.49), найдем множество наработок деталей агрегата.
Выбрав из совокупностей наработок минимальные значения, получим матрицу наработок агрегата на отказ
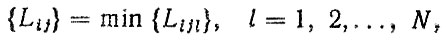 (6.50)
(6.50)
где N - число элементов, входящих в агрегат; Lij - i-я реализация наработки агрегата до j-го отказа. Из матрицы (6.50) после статистической обработки можно получить функции плотности распределения наработок и вероятности безотказной работы агрегата до первого и последующих отказов. Поток отказов агрегата находится суммированием потоков отказов деталей, определяемых из матрицы (6.49)
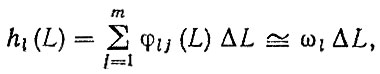 (6.51)
(6.51)
где φlj(L) - функция плотности распределения ресурса i-й детали до j-го отказа; ΔL - интервал пробега.
Рассмотрим моделирование характеристик надежности редуктора ведущего моста автомобиля с колесной формулой 6×4 и найдем его оптимальный по экономическому критерию ресурс, воспользовавшись, общей схемой решения подобных задач (рис. 6.5). Ведущий мост можно отнести к устройствам с последовательным соединением не восстанавливаемых элементов, заменяемых в случае отказа на новые. Характерной чертой взаимодействия элементов автомобильных трансмиссий, в том числе ведущего моста, является замена деталей сопряженных с отказавшими (например, пары шестерен). Надежность не сопряженных деталей молено считать независимой от надежности других элементов, К деталям, лимитирующим надежность ведущего моста относятся: шестерни главной передачи, подшипники, полуоси и сальники. За исключением сальников, все перечисленные элементы подвержены усталостным разрушениям и для расчета их ресурса можно воспользоваться формулой (5.35), Ресурс сальников будем полагать известным априори, установленным в результате испытаний опытной партии агрегатов, аналогичных проектируемым по назначению. Допустим, что их ресурс имеет логарифмически нормальное распределение с параметрами xл = 4,675, σл = = 0,804 [41].
Обобщенный нагрузочный режим редуктора в виде распределений ординат и амплитуд крутящего момента на полуоси и средней интенсивности нагружения [41] представлен на рис. 6.6. Характеристики нагруженности имеют соответственно нормальное (М = 700 Н⋅м, σM = 1100 Н⋅м), экспоненциальное (Мa = 340 Н⋅м) и релеевское с порогом чувствительности (σω = 75 цикл/км, ω0 = 330 цикл/км) распределения.
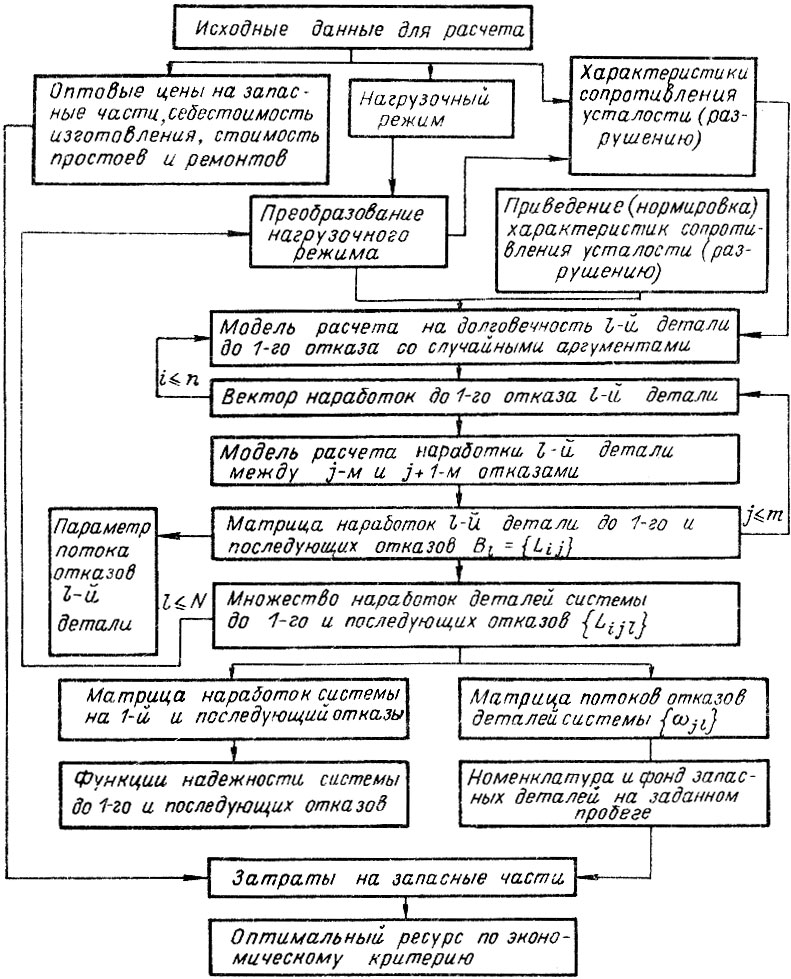
Рис. 6.5. Схема определения показателей надежности агрегата
Для расчета деталей редуктора по формуле (5.35) выполняются преобразования согласно (6.32) момента в напряжения - для полуосей и шестерен (6.24) и в эквивалентную силу-для подшипников (6.43).
Расчет коэффициентов пропорциональности kc и моделирование ресурса деталей осуществлялись на ЭВМ, Исходные данные для моделирования наработок до первого отказа перечисленных деталей представлены в табл. 6.10. Для каждой из деталей генерировалось по 500 случайных наработок, из которых формировались "эмпирические" распределения ресурса в виде гистограмм.
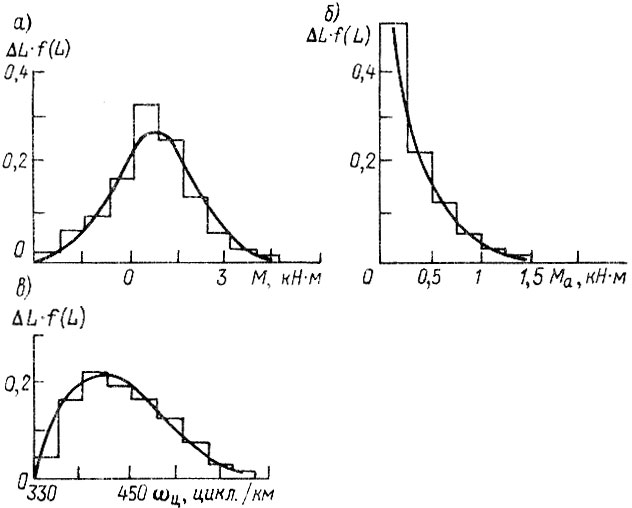
Рис. 6.6. Плотности распределения характеристик обобщенного нагрузочного режима трансмиссии: а - крутящий момент на полуоси; б - амплитуды крутящего момента на полуоси; в интенсивность нагружения в виде числа циклов на километр пути
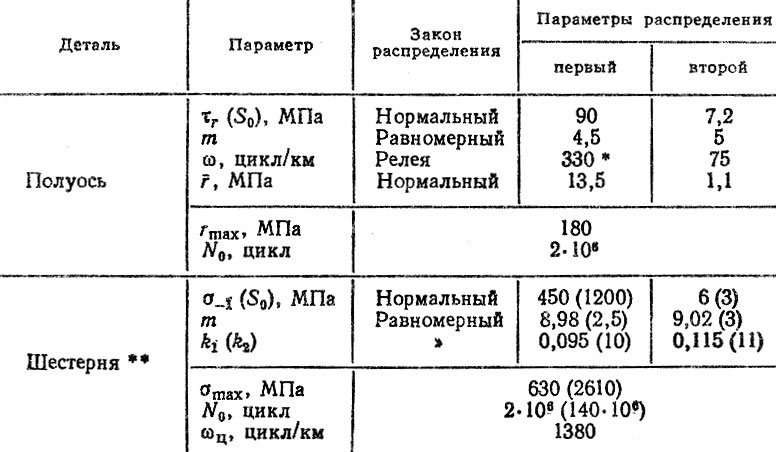
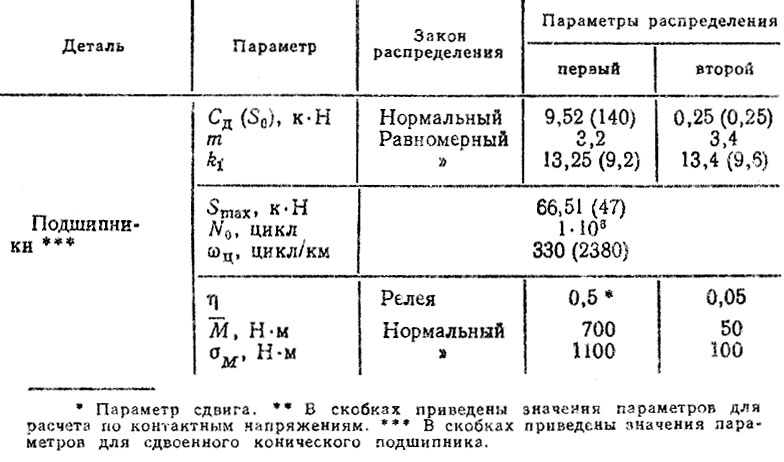
Таблица 6.10. Исходные данные для моделирования ресурса деталей ведущего моста
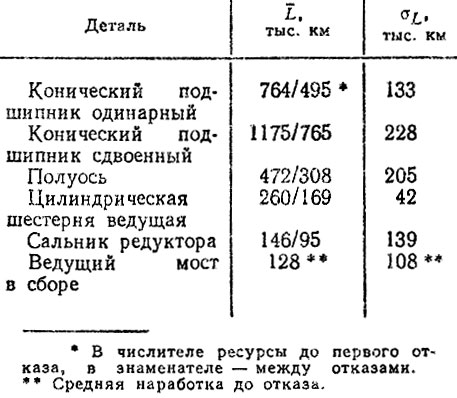
Таблица 6.11. Средние ресурсы ведущего моста и лимитирующие его надежность деталей, полученные моделированием
С учетом в ведущих мостах автомобиля формулы 6×4 нескольких однотипных элементов (четыре полуоси две главные передачи и т. п.) определялось распределение минимальных членов выборок в соответствии с моделью слабейшего звена (2.49) Lj = min {Li}, i = 1,2, ... , M , j = 1 , 2,..., 500, где M - число однотипных элементов в конструкции. Это же правило применялось при расчете шестерен на изгиб и по контактным напряжениям (М = 2). Наработки между отказами моделировались по закону, полученному из закона распределения ресурса до первого отказа с учетом поправки α = 0,65 на среднее значение. Последующие отказы определялись по формуле (8.48). Обработка полученных данных показала, что ресурс шестерен имеет нормальное, а полуоси и подшипников - логарифмически нормальное распределение (рис. 6.7). Смоделированный по правилу (6.50) ресурс всего агрегата имеет также логарифмически нормальный закон с параметрами хл = 4,587, σΛ = 0,73 (табл. 6.11). Вероятность безотказной работы ведущего моста представлена на рис. 6.8, На рис. 6.9 приведены параметры потоков отказов деталей и агрегата в целом, определенные согласно (6.51).
Для определения оптимального ресурса ведущего моста воспользуемся методикой" изложенной в третьей главе. Данные для расчета с учетом табл. 6.12 и оптовых цен на детали и ведущий мост в целом следующие: СА = 122 руб.; С = 7 руб.; σc = 8,3 руб.; L1 = 563 тыс. км; L2 = 366 тыс. км; σ1 = 371 тыс. км; σ12 = 299 тыс. км. По формулам (3.62)-(3.63) находим Ln = 548 тыс. км, Δ = -24,6 и β = 0,0956. Полагая зависимость для накопленных затрат степенной, по формулам (3.66)-(3.67) получим γ = 0,000174 и m = 1,9. Далее, приняв ak = 3 [39], найдем Rэ = 713 тыс. км и σR = 240 тыс. км.
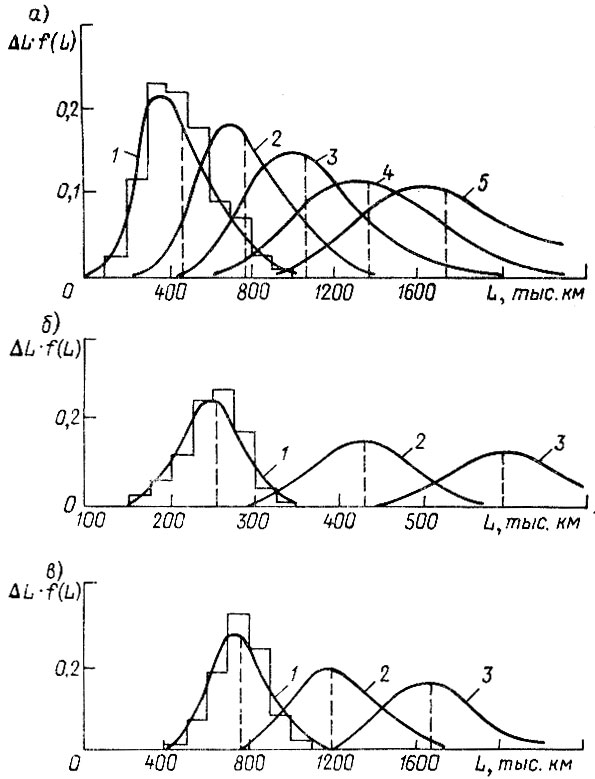
Рис. 6.7. Результаты моделирования ресурса полуоси (а), ведущей цилиндрической шестерни (б) и конического подшипника (в); 1-5 - порядковые номера отказов
По другой методике, заключающейся в вычислении потоков затрат по формулам (3.55)-(3.56) с учетом смоделированных потоков (рис. 6.9) суммарное накопленные затраты удовлетворительно аппроксимируются зависимостью СL = 0,00027L2,14 [40]. По формуле для оптимального ресурса получим R'э = 630 тыс, км.
Рассмотрим пример определения ресурса двигателя грузового автомобиля по техническому критерию, воспользовавшись износовой моделью долговечности сопряжений гильзы цилиндров-поршни" и "шейки коленчатого вала - вкладыши". Поскольку возможно восстановление работоспособности двигателя заменой поршневых колец и вкладышей, то, очевидно, его предельное состояние будет определяться предельно допустимыми износами гильз цилиндров и коренных либо шатунных шеек коленчатого вала.
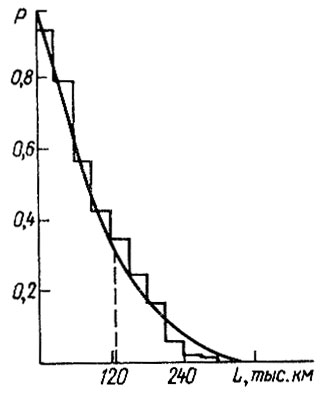
Рис. 6.8. Вероятность без отказной работы ведущего моста
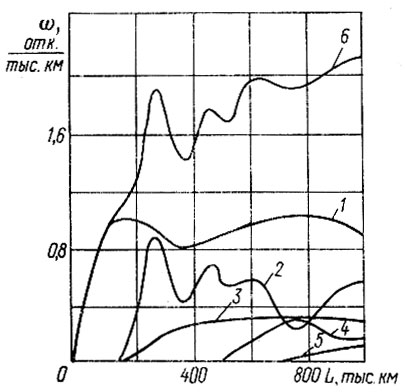
Рис. 6.9. Параметры потоков отказов деталей ведущего моста:
Используя линейную модель изнашивания (6.1) с учетом табл. 6.12 для гильзы цилиндра, получим
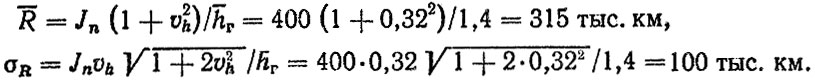
Так как в двигателе восемь гильз, то по формулам для минимальных значений (6.4-6.5) имеем для агрегата в целом
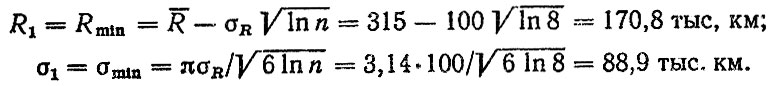
Выполнив аналогичным образом расчет ресурса двигателя по износу коренных и шатунных шеек, получим соответственно R2 = 179 тыс. км, 2 = 87 тыс. км, R3 = 193 тыс. км, σ3 = 112 тыс. км.

Таблица 6.12. Средние интенсивности износа и предельные состояния элементов двигателей грузовых автомобилей
Поскольку коэффициенты вариации ресурсов достаточно высоки, предположим, что для всех трех случаев справедлив закон распределения Вейбулла. Вычислив параметры распределений по найденным значениям Rш и σш и воспользовавшись моделью слабейшего звена (2.49), можно смоделировать на ЭВМ окончательное распределение ресурса двигателя до капитального ремонта по техническому критерию. Для рассматриваемого примера полученное после обработки распределение подчиняется закону Вейбулла с параметрами L0 = 3794 и m = 1,766 (RT = 95 тыс. км, σΤ = 55 тыс. км).
Для оценки ресурса двигателя по экономическому критерию воспользуемся результатами расчета по износу и априорными данными из работы [39] (табл. 6.13). Ресурс коленчатого вала определялся допустимыми износами коренных и шатунных шеек по изложенной выше методике. При расчете средних наработок до первого отказа цилиндро-поршневой группы брались результаты расчета на износ гильз цилиндров. Средние наработки между отказами для всех деталей находились по корреляционным уравнениям, отражающим статистическую связь между характеристиками ресурсов до первого отказа и между отказами (см. табл. 3.3). Наработки установлены с учетом комплектных замен коленчатого вала в сборе с коренными и шатунными вкладышами и цилиндро-поршневой группы вместе о гильзами, поршнями, поршневыми кольцами и пальцами.
Для расчета ресурса по формулам (3.68-3.70) воспользуемся корреляционными уравнениями и о учетом табл. 3.3 найдем:
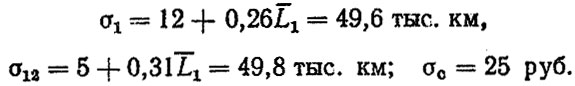
Полагая Сд = 450 руб, α = 0,9 и k = 1,5, по формулам (3.63- 3.67) вычислим m = 1,785 γ = 0,0195 и далее из (3.68-3.70) определим = 170 тыс. км и о, = 61,7 тыс. км.
Как видно из расчетов, ресурсы по экономическому и техническому критериям близки между собой. Применив снова правило "слабейшего звена" (2.49) для двух распределений f(RT) и f (Ra), считая их подчиненными закону Вейбулла, получим результирующее распределение Fэ (R) ресурса двигателя с учетом как технического, так и экономического факторов
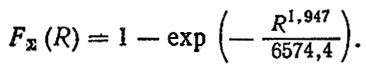
|
ПОИСК:
|
© MOTORZLIB.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'
При использовании материалов сайта активная ссылка обязательна:
http://motorzlib.ru/ 'Автомобилестроение, наземный транспорт и организация движения'