6.2. Расчеты на долговечность деталей трансмиссии

Зубчатые колеса. Зубчатые колеса коробки передач, раздаточных коробок и главных передач ведущих мостов грузовых автомобилей относятся к деталям, лимитирующим надежность. Для определения их долговечности необходимо выполнить следующие расчеты: на статическую прочность; на усталость при изгибе; на контактную усталость, на износ, включающий соответствующие оценки для различных сечений, в частности, зубьев, посадочных поверхностей, конусных поверхностей (при наличии синхронизаторов) и т. п.

Рассмотрим модель отказа зубчатых колес при условии независимости указанных разрушительных процессов. Согласно (2.50) имеем

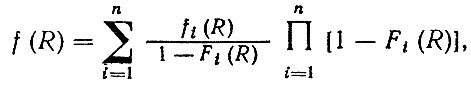(6.22)

где f (R) - плотность распределения ресурса зубчатого колеса; F_i (R), f_i (R) - соответственно функция и плотность распределения ресурса для i-го вида разрушительного процесса; n - число видов расчета, n = 4.

При наличии F_i (R), зависящих от наработки (времени), определение f_i (R) не вызывает затруднений и может быть выполнено численно. Если расчет на статическую прочность производится по моделям 1.2, 2.1, 2.2 (см. табл. 2.4), то вместо функции распределения f_i (R) получаем оценку вероятности безотказной работы р_с, не зависящей от наработки R. Тогда на основании теоремы о полной вероятности событий формулу для функции распределения ресурса зубчатого колеса можно записать в виде

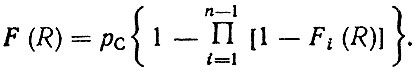(6.23)

Дифференцируя (6.23), получим формулу для плотности распределения f (R) аналогичную (6.22), но содержащую постоянный множитель р_с. Заметим, что для доведенных конструкций р_с ≈ 1 и ее можно не учитывать в формуле (6.23).

Поскольку модели расчета на износ зубчатых колес не отличаются от рассмотренных ранее для других деталей, то остановимся подробнее на расчете на усталость.

Для зубчатых колес трансмиссий автомобиля на основе ГОСТ 21354-75 разработана методика расчета изгибных и контактных напряжений [71].

Преобразования момента на валу в напряжения в зубьях осуществляются по формулам:

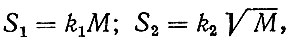(6.24)

где S₁, S₂ - соответственно напряжения изгибные и контактные, МПа; k₁, k₂ - коэффициенты преобразования; М - крутящий момент на валу зубчатого колеса, Н⋅м.

Коэффициенты k₁ и k₂ определяются по формулам:

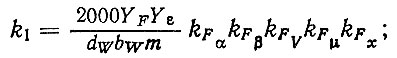(6.25)

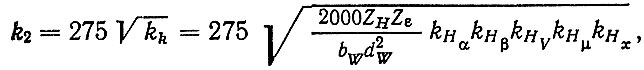(6.26)

где d_w, b_w - начальный диаметр и рабочая ширина венца шестерни; m - модуль зацепления; Y_F, Z_H - коэффициенты напряжений; Y_ε, Z_H - коэффициенты влияния перекрытия; k_Fα, k_Hα - коэффициенты интенсивности нагрузки; k_Fβ, k_Hβ - коэффициенты неравномерности распределения нагрузки; k_FV, k_HV - коэффициенты динамичности; k_Fμ, k_Hμ) - коэффициенты смазки; k_Fx, k_Hx - масштабные коэффициенты.

Подробные рекомендации по вычислению коэффициентов, входящих в формулы (6.25), (6.26), даны в работах [41, 54, 71].

Расчет на изгибную и контактную усталость производится в соответствии с блок-схемой (рис. 2.4), непосредственно по формуле (1.13) для трех вариантов ЛГСП с последующим выбором предпочтительного варианта по величине коэффициента а_р.

В расчете используется кривая усталости, соответствующая вероятности не разрушения Р = 0,5; при расчете на изгиб m_F = 9, N_0F = 4⋅10⁶ циклов, при расчете на контактную усталость - m_H = 6, N_0H = 1,2⋅10⁸; средние значения пределов выносливости: на изгиб

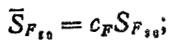(6.27)

на контактную усталость

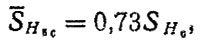(6.28)

где c_F - коэффициент, c_F = 1,09÷1,05; S_F90 - предел выносливости при Р = 0,9 и пульсирующем цикле нагружения; S_H0 - условный предел контактной выносливости зубьев, соответствующий базе испытаний N_0H = 107 циклов.

Плотность распределения ординат крутящего момента на валу зубчатого колеса представляется обобщенным нагрузочным режимом g (М). При этом не накладывается ограничений на вид законов распределения f_ik (М) и g (М).

Для зубчатых колес, нагруженных на всех передачах, расчет g (М) производится по формуле (6.29), а для зубчатых колес, нагруженных на одной передаче, обобщенный режим определяется по формуле (6.30)

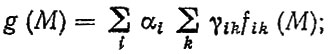(6.29)

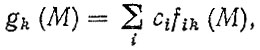(6.30)

где

Коэффициенты c_i позволяют выполнить условие нормировки для плотности распределения

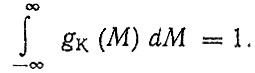
Однако для перехода к фактическим ресурсам, наблюдающимся в эксплуатации и определяемых пробегом автомобиля на всех передачах, в общую расчетную формулу ЛГСП (1.13) необходимо ввести коэффициент использования передачи (аналогично коэффициенту использования пробега η)

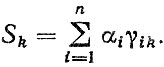(6.31)

Переход от моментов к напряжениям в общем виде выполняется с помощью преобразования случайных величин по формуле

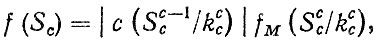(6.32)

где f (Sc) - плотность распределения напряжений (изгибных или касательных) в зубьях; f_M (S^c_c/k^c_c) - плотность распределения крутящего момента; с - коэффициент (с = 1 при расчетах на изгиб, с = 2 при расчетах на контактную усталость).

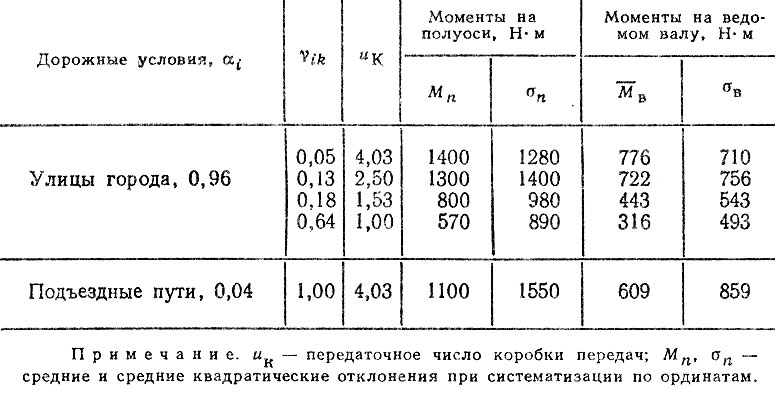
Таблица 6.3. Характеристики нагрузочных режимов автомобилей КамАЭ-5320, эксплуатировавшихся в АТП Главленавтотранса

Плотность распределения ресурса зубчатых колес определяется с помощью статистического моделирования либо параметры ресурса рассчитываются с использованием метода линеаризации, что позволяет учесть случайный характер всех величин, входящих в основную формулу (1.13) ЛГСП,

Рассмотрим пример прогноза ресурса шестерни четвертой передачи ведомого вала автомобиля КамАЗ, данные об экспериментально полученных нагрузочных режимах которых приведены в табл. 6.3.

Расчет на контактную и изгибную усталость выполняется в следующей последовательности.

1. Определяется обобщенный нагрузочный режим g (М). Для рассматриваемой шестерни c₁ = 1, c₂ = 0, т. е. g_k (М) = f_k (М). Допустим, что g_k (М) подчиняется нормальному закону распре-деления.

2. Рассчитываются коэффициенты преобразования k₁, k₂ крутящих моментов на ведомом валу в напряжении: по формулам (6.25), (6,26) находим k₁ = 0,335, k₂ = 44,14.

3. Определяются параметры кривых усталости. С учетом рекомендаций [41] находим: при расчете на изгиб S_F50 = 680 МПа; m_F = 9, N_0F = 4⋅10⁶; при расчете на контактную усталость S_H50 = 1470 МПа, m_H = 6, N_0H = 1,2-103.

4. Находятся максимальные S_max и минимальные S_min значения напряжений, учитываемых в расчетах по ЛГСП. Так, минимальные напряжения S_Fmin = 0,6 S_F50 = 400 МПа; S_Hmin = 0,6⋅S_H50 = 900 МПа. Максимальные значения определим из условия возникновения максимальных динамических моментов. С учетом формулы (5.38) при u_Σ = 1,53⋅7,21 = 11 и М_е = 650 Н⋅м находим М_max = 3274 Н⋅м, тогда S_Fmax = 1163 МПа, S_Hmax = 2524 МПа.

5. Рассчитываются коэффициент использования передачи S_k и число циклов нагружения ω_ц. По формуле (6.31) находим S_k = 0,96⋅0,18=0,17. Для определения ω_ц воспользуемся формулой

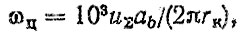
где u_Σ - общее передаточное число от вала зубчатого колеса до ведущих колес; a_b - число вхождений в зацепление одного зуба за один оборот вала.

При u_Σ = 11, a_b = 1, r_k = 0,454 м получим ω_ц = 2525 циклов на 1 км.

Таким образом, формулы для расчета средних ресурсов:

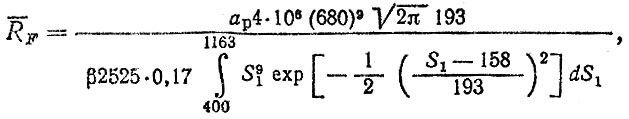(6.33)

на изгибную усталость

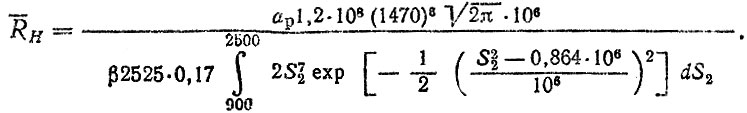(6.34)

Результаты расчета на усталость по трем вариантам гипотезы при β = 0,63 приведены в табл. 6.4. Оценка средних квадратических отклонений производилась с использованием формул линеаризации с учетом вариации четырех параметров: пределов выносливости (σ_SF, σ_SH), среднего и среднего квадратического отклонения нагрузочного режима (σ_M, σ_σ), а также стр.

Поскольку коэффициенты A_P < 0,4, то предпочтение должно быть отдано прогнозным вариантам II, III и III*.

Для расчета на износ по данным табл. 5.11 примем следующие параметры интенсивности изнашивания зубьев: m_u = 0,5 мкм/тыс. км; аи - 0,15 мкм/тыс. км. Тогда при допустимом износе I_д = 220 мкм по формулам (6.2), (6.3) получим прогнозные оценки ресурса шестерни четвертой передачи: R = 480 тыс. км, _R = 143 тыс. км.

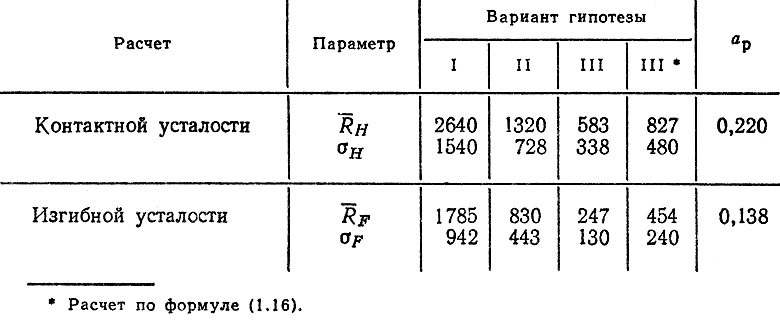
Таблица 6.4. Прогнозные оценки средних и средних квадратических отклонений ресурса шестерни четвертой передачи, тыс. км

Общая оценка ресурса шестерни по модели отказа с учетом контактной усталости и износа производится по формуле (6.23) при р_с = 1. Ввиду трудоемкости аналитического (численного) рас-чета определение параметров R_M и σM выполнено с помощью статистического моделирования путем формирования выборки минимальных значений R_j, определяемых соотношением

где R_i - случайные величины ресурса шестерни по износу, контактной или изгибной усталости.

Для расчетов R_I были взяты параметры ресурсов по изгибной и контактной усталости, соответствующие III*-му варианту (табл. 6.4). При моделировании учитывалось, что плотности распределения ресурса шестерни на изгиб и контактную усталость подчиняются распределению Вейбулла с параметрами: m = 2,0, R_0F - 512 (изгиб), m = 1,8, R_0H = 930 (контактная усталость). Обработка смоделированных значений позволила определить параметры ресурса шестерен: среднее значение R_M = 363 тыс. км, σ_M = 118 тыс. км.

КУД зубчатых колес коробок передач. Для прогноза среднего ресурса R воспользуемся КУД, учитывающим временной тренд, в виде

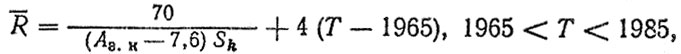(6.36)

где A_з.к - критерий долговечности, Н⋅м/мм; Т - год выпуска или существенной модернизации автомобиля; S_k - см. формулу (6.31).

Критерий A_з.к рассчитывается по формуле

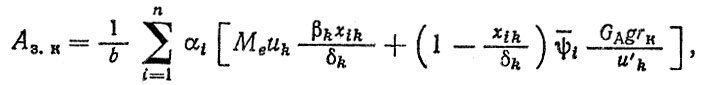(6.37)

где b - рабочая ширина зубчатого колеса, мм; М_е - максимальный крутящий момент двигателя, Н⋅мм; u_k, u'_k - передаточные числа трансмиссии соответственно от двигателя и от ведущих колес до вала шестерни. [Остальные обозначения даны в формулах (5.8), (5.11).]

На рис. 6.2 приведено КУД зубчатых колес при Т = 1965 г., построенное в виде A*_з.к = 7,6 + (70/R*), где R* = S_kR.

Выполним прогноз ресурса рассматриваемой шестерни при следующих значениях исходных данных. М_е = 650 Н⋅м, b = 30 мм, u_k = 1,38 (среднее значение для четвертой передачи с учетом делителя), u'_k = u₀ = 7,22; G_A = 26 500 кг; r_к = 0,454 м; δ_k = 1,06; по данным табл. 5.6, 5.9 для городских условий ψ₁ = 0,022, х₁₄ = 0,452, γ₁₄ = 0,4, для подъездных путей ψ₂ = 0,05, x₂₄ = 0, γ₂₄ = 0,33; β_k = 0,75.

Тогда критерий A_з.к = 8,36 Н⋅м/мм, S_k = 0,96⋅0,4 + 0,04⋅0,33 = 0,4; средний ресурс (при Т = 1976 г.) R = 220 тыс. км. По формуле (см. табл. 3.4) среднее квадратическое отклонение ресурса σ_R = 106 тыс. км.

Комбинированный прогноз. По оценкам ресурса шестерни с помощью модели отказа и КУД определим весовые коэффициенты комбинированного прогноза γ_i = 0,5, т. е. примем σ_M = σ_k = 112 тыс. км. Тогда средний ресурс R*_n = 292 тыс. км, σ*_n = 79 тыс. км, оценка непротиворечивости ε = 0,513. Допустим, что ресурс шестерни подчиняется нормальному закону распределения.

Наблюдение за подконтрольной партией автомобилей КамАЗ-5820 показали, что на пробегах 150-200 тыс, км не наблюдалось отказов шестерен. Это является косвенным подтверждением достоверности прогнозных оценок ресурса т. к. прогнозная вероятность отказа на пробеге 160 тыс, км составляет

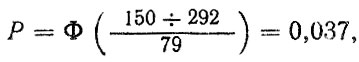(6.38)

где Φ (⋅) - интеграл вероятностей значения которого табулированы [8].

Подшипники качения (модель отказа). Для определения долговечности подшипников качения агрегатов транс-миссии (коробка передач, главной передачи и т. д.) и ходовой части (подшипники ступиц колес) необходимо выполнить несколько видов расчета: на статическую прочность, на контактную усталость, на износ, Также как для зубчатых колес при условии независимости указанных разрушительных процессов модель отказа подшипника качения может быть представлена в виде (6.22) или (6.23).

Наибольшее развитие получил расчет подшипников качения на контактную усталость по ЛГСП, Для примера в табл. 6.5 приведены результаты расчетов 90% ресурсов подшипников качения коробок передач автомобилей ЗИЛ-130, FA3-53 и МАЗ-500, выполненных на стадии проектирования указанных автомобилей по методике, разработанной под руководством И, С. Цитовича. Там же указаны фактические данные о 90%-ных ресурсах подшипников, полученных в результате наблюдений за эксплуатацией подконтрольных групп указанных моделей автомобилей. Разброс значений ресурсов объясняется, в частности, тем, что фактические значения соответствуют различным типам автомобилей (бортовые, самосвалы, тягачи), эксплуатировавшихся в различных условиях. Сопоставление расчетных и фактических данных с помощью коэффициента а = R_Р90/Р_Ф90 показывает, что среднее значение а = 1,3, т. е. близко к 1, но большой разброс величины а = 0,2÷4,0 говорит о том, что методика расчета требует дальнейшего совершенствования.

Рассмотрим методику расчета на усталостную долговечность подшипников качения [41], позволяющую оценить не только 90%-ный ресурс, но и другие показатели. Согласно блок-схеме, расчетная формула для среднего ресурса подшипника записывается в виде

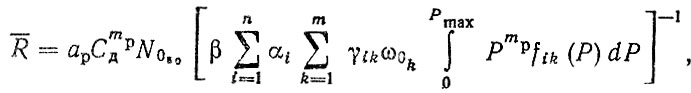(6.39)

где С_д - динамическая грузоподъемность, Н; N₀₅₀ - число циклов кривой усталости, соответствующее 50% вероятности не разрушения подшипника при нагрузке на подшипник, равной С_д; m_p - показатель (для шарикоподшипников m_p = 3, для ролико-подшипников m_p = 3,33); - частота нагружения подшипника при движении на k-й передаче; Р - приведенная нагрузка на подшипник, Н; f_ik (Р) - плотность распределения приведенной нагрузки при движении на k-й передаче в i-х условиях эксплуатации.

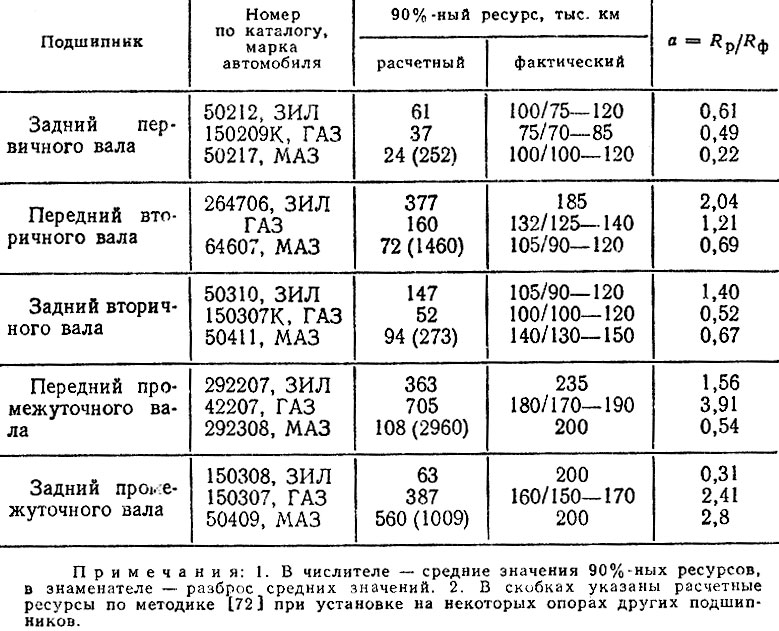
Таблица 6.5. Расчетные и фактические 90%-ные ресурсы подшипников коробок передач грузовых автомобилей (выпуска до 1970 г.)

Отметим основные особенности расчета на долговечность по формуле (6.39).

1. Поскольку для кривой усталости подшипников вместо предела выносливости вводится условная величина - динамическая грузоподъемность С_д, соответствующая вероятности не разрушения 90% при базовом числе N₀ = 10⁶ циклов [29], то для определения среднего ресурса необходимо перейти к кривой усталости, соответствующей вероятности не разгружения 50%. Воспользовавшись литературными данными и учитывая, что плотность распределения f(N₀) при нагрузке на подшипник, равной С_д, подчиняется закону Вейбулла [29], находим среднее значение N₀₅₀ = 4,7⋅10⁶ циклов.

2. Интегрирование в формуле (6.39) производится от нуля, а параметры кривой усталости - m_p, N₀₅₀ и С_д - не корректируются в зависимости от асимметрии нагрузочного режима. Это приводит к тому, что при условии ω_0k = const перестановка операций суммирования и интегрирования в формуле (6.39) не влияет на величину R. Следовательно, расчеты по обобщенному нагрузочному режиму g (Р) = Σα_iγ_ikf_ik(Р) и по отдельным нагрузочным режимам f_ik(Р) тождественны. Помимо этого расчет по второму варианту гипотезы совпадает с первым.

Если величины ω_0k существенно различаются, например для подшипников ведущего и промежуточного валов коробок передач, то расчет среднего ресурса R_ik производится раздельно для каждой передачи

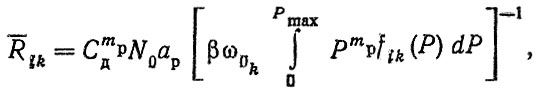(6.40)

а формула (6.39) может быть записана в виде

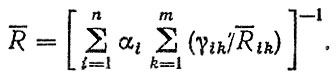(6.41)

3. Приведенная нагрузка на подшипник Р определяется по общепринятой формуле

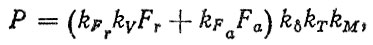(6.42)

где F_r, F_a - соответственно радиальная и осевая нагрузки; k_V - коэффициент вращения; k_δ - коэффициент безопасности; k_T - температурный коэффициент; k_M - коэффициент материала; k_Fr, k_Fa - соответственно коэффициенты радиальной и осевой нагрузок.

Приведенная нагрузка зависит от типа подшипников, способа их установки в опорах, а для коробок передач и главных передач также от количества, расположения и типа шестерен на валу. Так, для коробок передач используются в основном двухопорные конструкции подшипниковых узлов; трехопорные схемы применяются в редукторах ведущих мостов.

Подробные рекомендации по вычислению коэффицентов формулы (6.42), а, также осевых и радиальных нагрузок на подшипники даны в работах [29, 54, 72].

4. В общем виде зависимость между крутящим моментом на валу М и приведенной нагрузкой на подшипник может быть выражена в виде

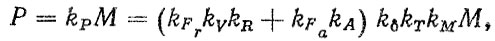(6.43)

где k_P - коэффициент преобразования; k_R, k_A - соответственно коэффициенты преобразования момента в суммарную радиальную и осевую нагрузки на подшипник.

При наличии плотности распределения крутящего момента f(М), схематизированного по способу ординат или пересечений, переход к плотности распределения f(Р) осуществляется по формуле (6.32) при с = 1.

Частота нагружения подшипника ω_0k, соответствует частоте его вращения и рассчитывается по формуле

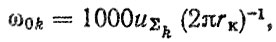(6.44)

где - общее передаточное число трансмиссии от вала до ведущих колес автомобиля при включении k-й передачи.

5. Расчет плотности распределения ресурса подшипника и его параметров производится методом статистического моделирования или с использованием формул линеаризации.

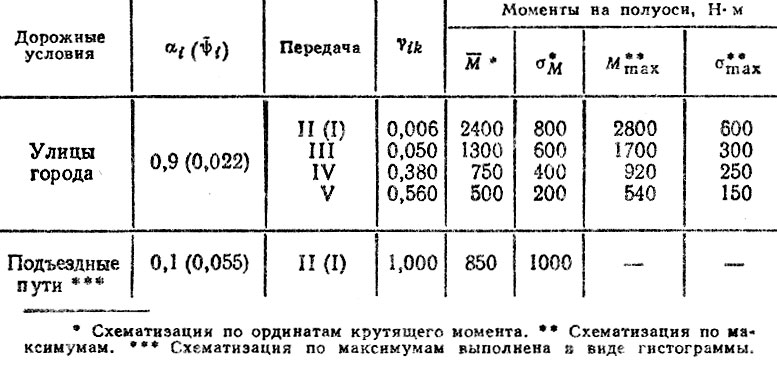
Таблица 6.6. Характеристика нагрузочных режимов авгомобилей-сатосаажв ЗИЛ-ММЗ-555

Изложенная методика была применена для оценки ресурсов радиально-упорных подшипников ведущей конической шестерни главной передачи автомобилей-самосвалов ЗИЛ-ММЗ-555 [41 ] и автомобилей КамАЭ-5320 [40], эксплуатировавшихся на строительных объектах Ленинграда.

Выполним прогнозный расчет ресурса шарикового подшипника № 150212 первичного вала (заднего) коробки передач автомобиля ЗИЛ-ММЗ-555. Данные об условиях эксплуатации и нагрузочных режимах подконтрольной партии автомобилей при-ведены в табл. 6.6.

Параметры кривой усталости подшипника с_д = 41 кH; N₀₅₀ = 4,7⋅10⁶ циклов; m_p = 3.

При расчете коэффициентов kP по формуле (6.43) было принято k_δ = 1,5, k_Τ = k_M = 1. Коэффициенты k_R и k_A рассчитывались по общепринятой методике 164" 721 о учетом параметров зубьев и геометрических размеров коробки передач. Средние значения Р и средние квадратические отклонения Р приведенных нагрузок на подшипник по передачам даны в табл. 6,7.

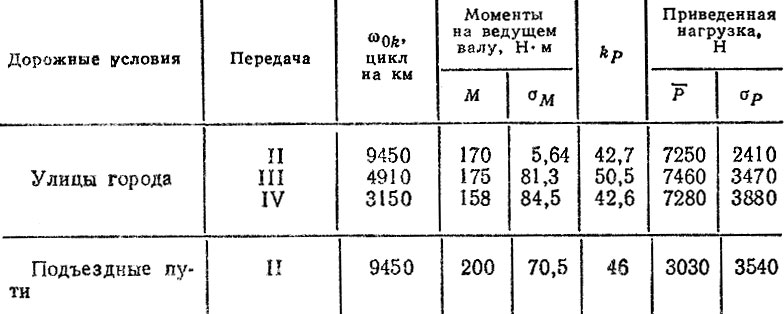
Таблица 6.7. Параметры приведенных нагрузок на подшипник 150212 коробки передач автомобиля ЗИЛ-ММЗ-555

Таблица 6.8. Результаты расчетов средних ресурсов и общего ресурса R подшипника 150212, тыс. км

При подстановке в формулу (6.40) данных табл. 6.7 при β = 0,5 с помощью численного интегрирования находим оценки средних ресурсов R_ik при движении на каждой передаче для различных вариантов гипотезы (табл. 6.8). Оценка общего ресурса подшипника с учетом коэффициентов α_i и γ_ik производится по формуле (6.41). В частности, для варианта III* имеем

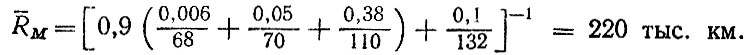
Воспользовавшись методом линеаризации получим σ_M = 81,5 тыс. км.

КУД подшипников коробки передач. Для прогноза среднего ресурса подшипников R₅₀ было получено КУД в виде

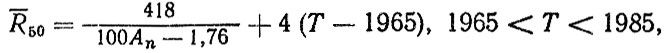(6.45)

где А_n - критерий долговечности; Т - год выпуска или существенной модернизации конструкции.

Критерий А_n рассчитывается по формуле

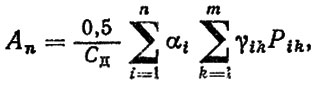(6.46)

где P_ik - приведенная нагрузка на подшипник при движении на k-й передаче в i-x условиях; С_д - динамическая грузоподъемность.

При расчете подшипников передней опоры ведущего вала учитывались только радиальные нагрузки, я вместо С_д подставлялась статическая грузоподъемность С₀.

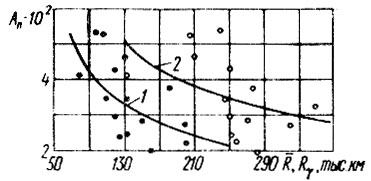
Рис. 6.3. Корреляционные уравнения долговечности подшипников коробок передач: 1 - для 90%-ных ресурсов; 2 - для средних ресурсов

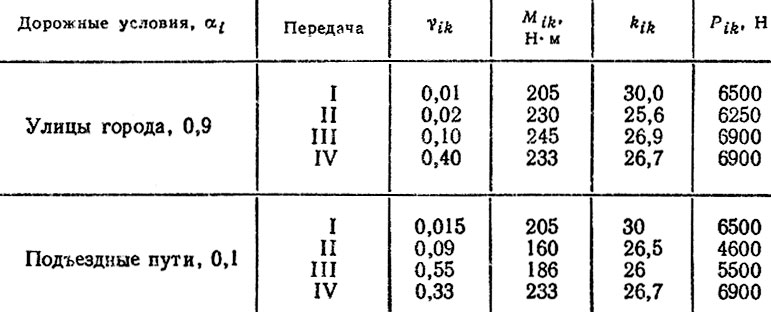
Таблица 6.9. Приведенные нагрузки на подшипник 150212 (для расчета критерия A_n)

Расчет P_ik производится по формуле, аналогичной (6.37),

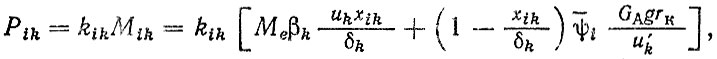(6.47)

где k_ik = k_Frk_Vk_R + k_Fak_A, см. формулу (6.43).

На рис. 6.3 приведены два варианта КУД подшипников коробки передач (при Т = 1965): первый вариант для средних ресурсов в виде A*_n = 100 = 3,76 + (418/R), корреляционное отношение η = 0,45, σ_А = 1,0; второй вариант - для 90% ресурсов в виде А*_n = 1,1 + (296/R_γ), η = 0,62, σ_А = 0,9,

Для рассматриваемого подшипника в результате расчетов нашли А_n = 0,0467 (табл. 6.9). Тогда, по формуле (6.45) при Т = 1965 имеем R = 141 тыс. км. По данным табл. 3.4 среднее квадратическое отклонение σ_R = 65 тыс. км.

Комбинированный прогноз. По оценкам ресурса подшипника о помощью модели (для варианта III* R_M = 220 тыс. км; σ_M = 81,5 тыс. км) и КУД определим весовые коэффициенты γ_i. При расчете по формуле (2.80) γ₁ = 0,61, тогда R = 190 тыс. км, σ_R = 60 тыс. км; при расчете по формуле (2.79) γ₁ = 0,39, R = 172 тыс. км, σ_R = 51 тыс. км; оценка непротиворечивости ε = 0,50. Фактические параметры ресурса указанных подшипников следующие: R_Φ = 210 тыс. км., σ_Φ = 60 тыс. км.