Глава 6. Примеры прогнозирования показателей надежности деталей и агрегатов автомобиля

6.1. Расчеты на долговечность деталей цилиндро-поршневой группы двигателя

К деталям, лимитирующим надежность двигателей, в первую очередь относятся детали цилиндро-поршневой группы и криво-шипно-шатунного механизма, отказы которых в основном связаны с износом. Известно [16, 18, 471, что на износ деталей двигателя влияет совокупность факторов, главнейшими из которых являются свойства трущихся материалов (физико-механические, химические), режимы работы (скоростные, нагрузочные, тепловые), геометрические параметры (форма, размеры, шероховатость поверхности), смазка (количество, очистка, подвод). По- скольку в настоящее время отсутствуют аналитические зависимости, позволяющие учесть многообразие указанных факторов, то за основу прогнозных методов оценки показателей долговечности принимаются экспериментальные материалы по видам износа и характеристикам изнашивания существующих конструкций двигателей, которые подлежат уточнению по мере поступления информации о результатах испытаний новых конструкций.

Рассмотрим методику прогноза показателей долговечности деталей двигателя на примере гильзы цилиндра.

Модель отказа. При построении модели отказа гильз цилиндров учтены следующие факторы: у большинства гильз цилиндров имеются участки максимального износа, соответствующие положению первого поршневого кольца в верхней мертвой точке; для гильз цилиндров одного двигателя наблюдается значительная неравномерность средне-максимальных износов. Так, в работе [161 отмечается 4-кратное расхождение в износах гильз цилиндров.

Поскольку для серийных двигателей данные об износах гильз обобщены в виде интенсивностей изнашивания (табл. 5.10), то модель износа представляется в виде

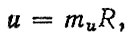(6.1)

где m_u - случайная величина интенсивности изнашивания, мкм/тыс. км; R - наработка (пробег) автомобиля, тыс. км.

Воспользовавшись уточненным методом линеаризации, выпишем формулы для среднего R и среднего квадратического отклонения σ_R ресурса!

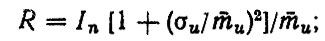(6.2)

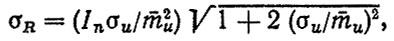(6.3)

где I_n - предельное значение износа, мкм; σ_u - среднее квадратическое отклонение интенсивности изнашивания, мкм/тыс. км.

Допустим, что замена гильз (или расточка цилиндров) производится при достижении предельного износа одной из них. Тогда в соответствии с моделями отказа детали (см. п. 2.4) для расчета ресурса необходимо воспользоваться формулами для распределений минимальных значений. В частности, для нормального закона с параметрами R, σ_R имеем:

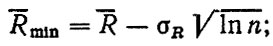(6.4)

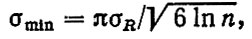(6.5)

где R_min, σ_min - соответственно оценки минимальных среднего и среднего квадратического отклонения, тыс. км; n - число гильз цилиндров двигателя.

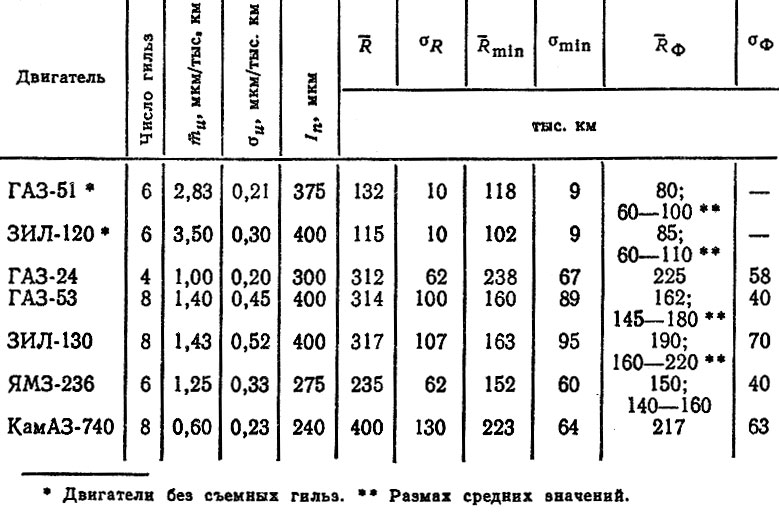
Таблица 6.1. Исходные данные результаты расчетов и фактические ресурсы гильз цилиндров автомобильных двигателей

В табл. 6.1 приведены исходные данные и оценки ресурсов гильз цилиндров, рассчитанные по формулам (6.2)-(6.5); там же даны фактические ресурсы по результатам наблюдений за под-

контрольными партиями автомобилей. Из сопоставления R_ьшт и R_Φ можно сделать вывод об их удовлетворительном согласии.

Выполним прогноз ресурса гильз дизельного двигателя КамАЗ-740 выпуска 1976 г. По данным Кугеля Р. В., для цилиндров дизельных двигателей выпуска 1948 г. m_u = 6,3 мкм/тыс. км, гильз цилиндров двигателей выпуска 1965 г. m_u = 1,25 мкм/тыс. км. Тогда приближенная зависимость m_u от времени выпуска может быть записана в виде

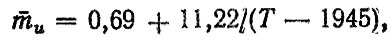(6.6)

где Т - год выпуска новой модели.

При подстановке Т = 1976 г. В формулу (6.6), находим m_u = 1,05 мкм/тыс. км. Тогда при σ_u = 0,315 мкм/тыс. км получим R_min = 142 тыс. КМ, σ_min = 66,3 тыс. км.

Уточним прогнозные оценки. В результате проведенных замеров для подконтрольной партии оказалось m_u = 0,6 мкм/тыс. км, σ_u = 0,23 мкм/тыс. км. Эти данные хорошо согласуются с результатами, приведенными в работе [38] - m_u = 0,6÷0,73 мкм/тыс. км. Сопоставляя результаты прогноза (см. табл. 6.1) для двух указанных случаев, отметим, что предпочтение должно быть отдано оценке R_min = 223 тыс. км, так как при расчете по формуле (6.6) m_u определено лишь по двум точкам.

Оценим среднюю ошибку прогноза среднего ресурса, полученного с помощью модели отказа, по формуле

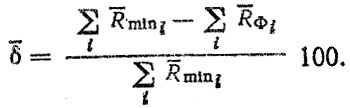(6.7)

По данным табл. 6.1 находим 8-5%.

КУД гильз цилиндров. В соответствии с методикой построения КУД (см. п. 2.5) была собрана и обработана статистическая информация, необходимая для расчета критерия долговечности гильз цилиндров Α_Γ, который в результате проведенного поиска был представлен в виде

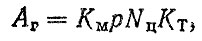(6.8)

где К_M - коэффициент, отражающий физико-механические свойства материалов; р - параметр, характеризующий силовой и скоростной режимы нагружения гильз; N_ц - число циклов нагружения гильзы за 1 км пробега автомобиля; К_т - коэффициент, отражающий тепло-напряженность детали.

Коэффициент К_M рассчитывается по формуле [32]

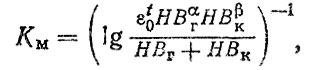(6.9)

где НВ_Г, НВ_К - твердость по Бринелю соответственно гильзы цилиндра и кольца; ε₀ -относительное удлинение материала, %; t - показатель фрикционно-контактной усталости; α, β - коэффициенты.

Исходные данные для расчета К_М приведены в табл. 6.2; для расчетов можно принять К_M = 0,169÷0,174 (карбюраторные двигатели), К_М = 0,152 (дизельные двигатели).

В качестве параметра р выбрано удельное давление кольца на стенку цилиндра [21]

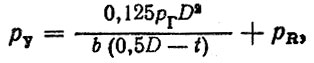(6.10)

где р_Γ - текущее значение давления газов за кольцом, МПа; D - диаметр цилиндра, дм; b - высота сопрягаемой с цилиндром части кольца, дм; t - радиальная толщина кольца, дм.

Таблица 6.2. Исходные данные дли расчета коэффициентов K_M гильз цилиндров, поршневых колец и поршней [32]

.

Удельное давление p_R, создаваемое упругой силой кольца, определяется по формуле

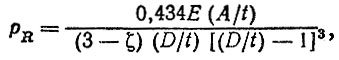(6.11)

где Е - модуль упругости, МПа; А - зазор в замке кольца в свободном состоянии, дм; ζ - постоянная, зависящая от эпюры давления, принято в расчетах ζ = 0,2.

Расчет pΓ производится по формуле

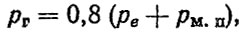(6.12)

где р_e - среднее эффективное давление, МПа; р_{м. п} - давление механических потерь, МПа.

При расчете р_е учитываются условия эксплуатации автомобилей, различные виды дорог α_i, загрузка Q_j, средние скорости движения автомобиля υ_ij, влияние неустановившихся режимов.

Расчетная формула для ре следующая:

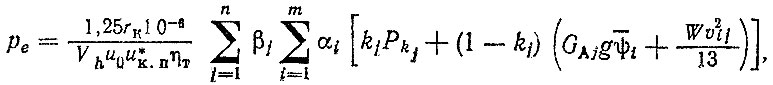(6.13)

где r_k - радиус колеса, м; V_h - рабочий объем цилиндров двигателя, л; u₀ - передаточное число главной передачи; u*_к.п - средневзвешенное значение передаточного числа коробки передач; η_т - КПД трансмиссии; k_j - коэффициент учета неустановившихся режимов движения; β_j - коэффициент использования пробега; Р_kj - тяговая сила на ведущих колесах, Н [формула (5.8)]; G_Aj - масса автомобиля, т; ψ_i - коэффициент сопротивления движению; W - фактор обтекаемости автомобиля? Н×(с/м)².

Учет неустановившихся режимов производился только для условий эксплуатации в городе (коэффициент k_j = 0,2) [71]. При расчете P_kj. использовалось передаточное число передачи u_Κ, на которой производится трогание автомобиля: для груженого с четырех ступенчатой коробкой передач - первая, с пяти-ступенчатой - вторая; для не груженого автомобиля - среднее значение для первой и второй передач.

Величина u*_{k. п} определяется по формуле

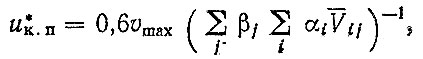(6.14)

где υ_max - максимальная скорость автомобиля; V_ij - средняя скорость автомобиля в i-x дорожных условиях при j-й загрузке.

Ввиду отсутствия точной информации коэффициенты β_j выбраны на основании статистических данных по РСФСР за период 1970-1978 гг.: для грузовых бортовых автомобилей и седельных тягачей β_j = 0,63, для самосвалов β_j = 0,5,

Давление механических потерь p_Μ.Π рассчитывается по формуле

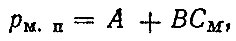(6.15)

где A, В - коэффициенты (для карбюраторных двигателей А = 0,04, В = 0,02; для дизельных А = 0,05, В = 0,027 [2]).

Для определения средней скорости поршня воспользуемся выражением

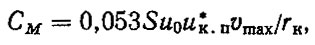(6.16)

где S - ход поршня, м.

Число циклов нагружения гильзы N_ц за 1 км пробега рассчитывается по формуле

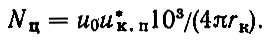(6.17)

Оценка тепло-напряженности деталей цилиндро-поршневой группы производится с помощью коэффициента K_т, представляющего собой отношение коэффициентов тепло-напряженности для заданных условий эксплуатации К_т.э. Для максимальной мощности двигателя K_тmax ,

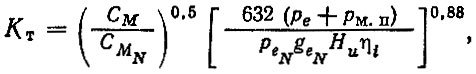(6.18)

где C_MN, g_eN, p_eN - средняя скорость поршня, удельный расход топлива и среднее эффективное давление при максимальной мощности; H_u - теплотворная способность топлива; η_i - индикаторный КПД (для карбюраторных двигателей η_i = 0,31, для дизельных η_i = 0,45).

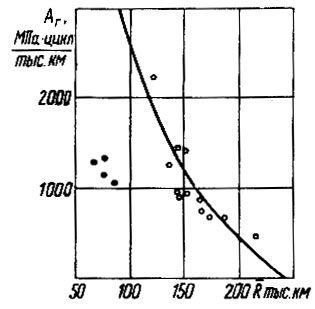
Рис. 6.1. Корреляционное уравнение долговечности гильз цилиндров: o - двигатели первой группы; o - двигатели второй группы

С учетом вышеизложенного размерность критерия A_Γ определяется р и N_ц и выражается в МПа. цикл на 1 км пробега.

Расчеты критериев А_Γ выполнялись для двигателей двух групп автомобилей: в первую группу вошли автомобили ГАЗ-51, ЗИЛ-164А, ЗИЛ-ММЗ-164АН и автобус ЛАЗ-695Б выпуска 50-х годов, во вторую -- 11 автомобилей (ЗИЛ, ГАЗ, МАЗ, КрАЗ) и автобус ЛАЗ-677 выпуска 60-х годов. КУД гильз цилиндров рассчитано для второй группы (рис. 6.1).

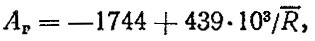(6.19)

где R - средний ресурс гильз, тыс. км.

Среднее квадратическое отклонение σ_Γ = 270 МПа⋅цикл, корреляционное отношение η = 0,85.

Ввиду малого объема первой группы для нее не удалось рассчитать КУД, но данные по критериям А_Γ были использованы для построения прогнозного тренда гильз цилиндров;

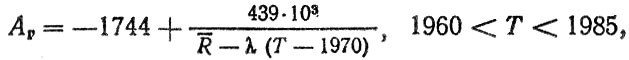(6.20)

где Т - год начала выпуска или существенной модернизации автомобиля; λ - коэффициент (в расчетах λ = 6).

Выполним прогноз среднего ресурса гильз цилиндров автомобилей КамАЭ-5320 выпуска 1976 г. (наблюдение за подконтрольной партией автомобилей производилось в АТП Ленинграда). Параметры, характеризующие условия эксплуатации, приведены в табл. 6.2; G_ag = 255 кН, G_a0 = 121 кН, η = 0,63.

По формуле (6.11) при D = 1,2 дм, t = 0,05 дм, А = 0,188 дм и Е = 1,2×10⁵ МПа находим удельное давление p_R = 0,234 МПа.

При υ_max = 100 км/ч, u_{к. п} = 1,69 [формула(6.14)]. Средняя скорость поршня при S = 0,12 м, u₀ = 5,94 и r_k = 0,454 м С_м = 8,33 м/с; давление механических потерь [формула (6.15) ]

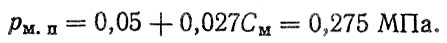
Средне-эффективное давление р_е [формула (6.13)1 при V_h = 10,65 л, η_т = 0,9, W = 4,1 Н(с/м)² и данных табл. 6.2 р_е = 0,392 МПа.

По найденным значениям p_R, р_M и р_е определим параметр р (при b = 0,03 дм)

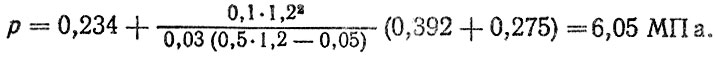
Число циклов нагружения гильз за I км пробега [формула (6.17)] N_ц = 1760. Коэффициент тепло-напряженности (при C_MN = 12,4 м/с, p_eN = 0,66 МПа, g_eN = 0,175 г/л. о. ч. и H_u = 10 500 ккал/кг) k = 0,653.

Таким образом, критерий долговечности Аг - 1056 МПа. цикл.

Средний прогнозный ресурс гильз цилиндров [формула (6.20)] до первого отказа

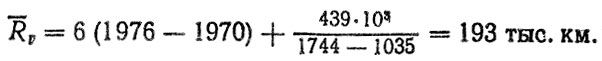
Оценку среднего квадратического отклонения ресурса σ_R выполним с помощью уравнения (см. табл. 3.3)

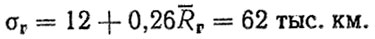
Комбинированный прогноз. Выполним синтез прогнозов ресурса гильз цилиндров, полученных с помощью модели отказа (R_M = 223 тыс. км, σ_M = 64 тыс. км) и КУД (R_Γ = 193 тыс. км, σ_Γ = 62 тыс. км). Допустим, что плотности распределения ресурсов f_M (R) и f_Γ(R) подчиняются нормальным законам распределения и _M = σ_Γ = 63 тыс. км.

Согласно методике (см. п. 2.6), весовые коэффициенты γ₁ = ₂ = 0,5; параметры комбинированного прогноза: среднее значение R* = 208 тыс. км; среднее квадратическое отклонение

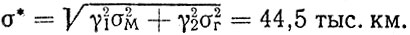
Для оценки непротиворечивости вариантов из решения уравнения f_М (R) = f_Γ(R) необходимо найти точки пересечения R_ci плотностей распределений f_м (R) и f_Γ (R). При σ_M = σ_Γ и нормальных законах f_M (R) и f_Γ (R) получаем частный случай общей зависимости [41], согласно которой R_c = R*. Тогда мера непротиворечивости

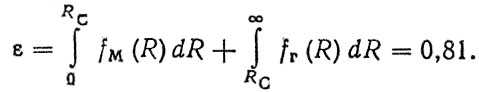(6.21)

Сопоставляя результаты комбинированного прогноза и данные о ресурсах гильз подконтрольной партии автомобилей КамАЗ (см. табл. 6.1), следует отметить их хорошее совпадение. В работе [42] приведены примеры прогноза ресурса деталей цилиндро-поршневой группы и кривошипно-шатунного механизма с использованием КУЦ и моделей отказа.