5.3. Обобщенные нагрузочные режимы деталей автомобиля

Из теории автомобиля и результатов многочисленных экспериментальных исследований следует, что нагрузочные режимы (силовые, скоростные, тепловые и т. п.) существенно изменяются в зависимости от условий эксплуатации. Очевидно, наиболее достоверным является эксплуатационный нагрузочный режим детали, зафиксированный на пробеге до ее отказа. В этом случае спектр нагрузок отражает не только всю совокупность условий эксплуатации, но и изменения технического состояния автомобиля.

Если нагрузочный режим получен на отдельных участках конечной длительности, то предположение о неизменности его параметров (стационарности) при увеличении длительности пробега носит гипотетический характер. Учитывая трудности записи и обработки нагрузочных режимов большой длительности серийных конструкций, при расчете нагрузочных режимов на стадии проектирования приходится идти на определенные допущения и упрощения. Так, в работе [41] было показано, что предположение о независимости нагрузочных режимов в различных условиях эксплуатации не всегда отвечает характеру накопления повреждений. В частности, при расчетах на усталость расчленение нагрузочного режима на отдельные составляющие равносильно подсчету долговечности от каждой ступени блока и последующему их суммированию, что соответствует линейной гипотезе накопления повреждений лишь для нагрузок выше предела выносливости.

Усталостная долговечность деталей автомобиля, эксплуатирующегося в различных дорожных условиях, в случае независимости нагрузочных режимов рассчитывается по формуле

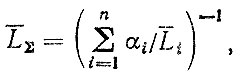(5.20)

где L_Σ - средний ресурс в смешанных условиях эксплуатации; α_i - долевой коэффициент пробега в i-x дорожных условиях; L_i - средний ресурс детали в i-х условиях"рассчитываемый по формуле (1.13).

Вывод формулы (5.20) основывается на том, что вероятность разрушения детали при пробеге в i-x условиях эксплуатации равна

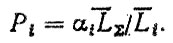
При условии

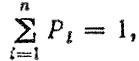
справедливом для независимых событий, приходим к формуле (5.20). При расчете по (5.20) предполагается, что каждым i-м условиям эксплуатации соответствует свой нагрузочный режим, а параметры кривой усталости остаются неизменными либо корректируются с учетом i-го нагрузочного режима.

Однако такой подход противоречит результатам стендовых испытаний с программным и случайным нагружениями [30], Согласно программным испытаниям с блоками, содержащими ступени как выше, так и ниже предела выносливости, доказано, что нагрузки ниже предела выносливости также участвуют в накоплении усталостных повреждений. Аналогичная картина наблюдается и при случайном нагружении. Поэтому более корректным, на наш взгляд, является не разделение нагрузочных режимов для каждого из i-x условий эксплуатации, а представление их в виде обобщенного нагрузочного режима и единой откорректированной кривой усталости.

Под обобщенным нагрузочным режимом будем понимать такой режим, который отражает заданные условия эксплуатации автомобилей в виде удельных показателей: плотности распределения g (S), среднего числа циклов на единицу пути ω и т. д. Обобщенный режим включает элементарные режимы и представляется в виде суперпозиции этих режимов, при этом коэффициенты суперпозиции определяются по результатам длительных эксплуатационных испытаний или моделирования условий движения автомобиля. Под элементарным нагрузочным режимом понимается такой режим, который не может быть разложен на более простые составляющие (либо такое разложение нецелесообразно). Примерами элементарных нагрузочных режимов являются трогание автомобиля на k-й передаче на дороге i-й о типа с j-й загрузкой; движение на k-й передаче с j-й скоростью на дороге i-го типа с j-й загрузкой и т. д.

Плотность распределения крутящего момента g (S) и среднее число циклов нагружения ω для обобщенного режима определяются по формулам (для одного весового состояния автомобиля):

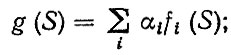(5.21)

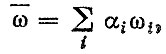(5.22)

где f_i (S), ω_i - соответственно плотность распределения нагрузочного режима и среднее число циклов для i-х условий эксплуатации.

Воспользовавшись формулами для суперпозиции законов распределения, находим параметры обобщенного нагрузочного режима:

среднее значение

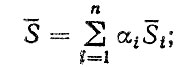(5.23)

среднее квадратическое отклонение

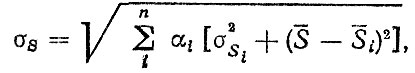(5.24)

где S_i, σ_Si - соответственно среднее значение и среднее квадратическое отклонение нагрузочного режима в i-x условиях.

Корректировка параметров кривой усталости производится по следующим формулам: предел выносливости

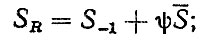(5.25)

параметр кривой

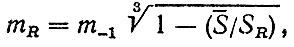(5.26)

где ψ - коэффициент учета асимметрии [30]; S_-1, m_-1 - предел выносливости и параметр кривой соответствующие симметричному циклу.

Верхняя граница повреждающих напряжений S_max определяется при решении уравнения

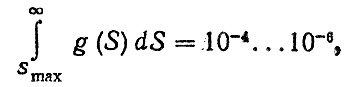(5.27)

но с учетом условия S_max ≤ lS_T, где S_Т - предел прочности (текучести); I - коэффициент, I = 0,8÷0,9.

Минимальное напряжение, учитываемое в расчете,

(5.28)

где k = 0,6.

Корректирующий коэффициент ар рассчитывается по формуле (1.14) при подстановке g (S).

Таким образом, формула для расчета среднего ресурса в смешанных условиях эксплуатации запишется в виде (при степенной зависимости для кривой усталости)

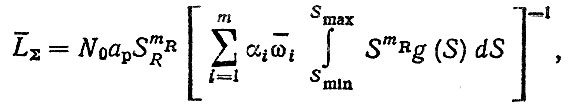(5.29)

где S_R, m_R, S_max, S_min, g (S) - определены по формулам (5.21)-(5.25)-(5.28).

В зависимости от степени учета влияния корректировки на параметры кривой усталости возможны различные модификации формул (5.20) и (5.29).

Для примера в табл. 5.17 приведены результаты расчетов средних ресурсов полуоси и рессоры по независимым и обобщенным нагрузочным режимам, из которых видно их значительное расхождение. Практически в большинстве случаев при расчете по формуле (5.20) средние значения ресурсов выше, чем при расчете по формуле (5,29). Следует отметить, что результаты расчетов совпадают при S_R = S_min = 0, например, для подшипников качения.

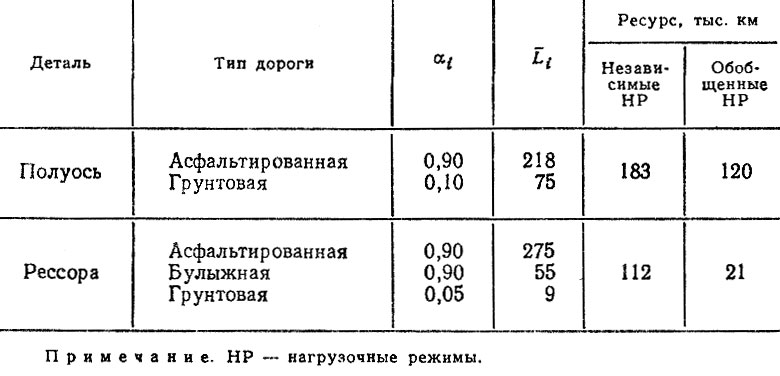
Таблица 5.17. Средние ресурсы деталей автомобиля, эксплуатируемого в различных дорожных условиях

Обобщенные нагрузочные режимы могут быть рассчитаны для любых деталей автомобиля. Рассмотрим подробнее их определение на примере деталей трансмиссии, нагруженных на разных передачах.

Плотность распределения крутящего момента g (S) для обобщенного нагрузочного режима определяется по формуле

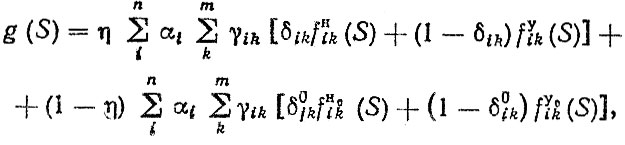(5.30)

где η - коэффициент использования пробега; γ_ik и f_ik (S) - долевой коэффициент пробега и плотности распределения крутящего момента на k-й передаче и i-м типе дорожного покрытия; δ_ik - коэффициенты, отражающие соотношение установившихся (стационарных) и неустановившихся (нестационарных) нагрузочных режимов (индексы "н" и "у" относятся соответственно к не установившемуся и установившемуся нагрузочным режимам, индекс "О" относится к порожнему автомобилю).

Параметры нагрузочного режима - S и σ_s - рассчитываются по формулам (5.23) и (5.24). Аналогично определяются параметры для числа циклов.

Если с помощью g (S) производится оценка статической прочности, то в качестве f_ik(S) используются плотности распределения предельных значений случайных величин (см. п. 2.3). При описании g (S) распределением максимумов III типа

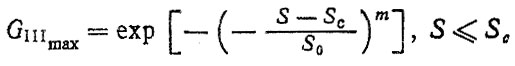(5.31)

величина S_c для деталей трансмиссии автомобиля может быть определена по эмпирической формуле

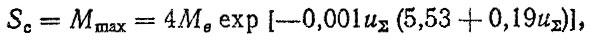(5.32)

где М_max - максимальный крутящий момент, приведенный к первичному валу, Н⋅м; М_е - максимальный момент двигателя (номинальный), Н⋅м; u_Σ = u_ku₀, u_k, u₀ - соответственно передаточные числа коробки передач и главной передачи.

Для однозвенных и многозвенных колебательных систем, эквивалентных трансмиссии автомобиля, расчет М_max производится с применением цифровых и аналоговых вычислительных машин.

При оценках усталостной долговечности, если для расчета М (t) используются нагрузочные режимы, схематизированные по способу ординат или пересечений (например, для шестерен или подшипников), то коэффициенты γ_ik отражают долю движения автомобиля по пути, а оценка числа циклов нагружения производится по известным формулам с учетом радиуса колеса автомобиля r_к и передаточных чисел коробки передач и главной передачи. При схематизации нагрузочного режима по экстремальным точкам процесса (максимумы, полные циклы и т. д.) коэффициенты γ_ik необходимо откорректировать с помощью формулы

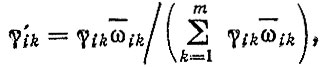(5.33)

где ω_ik - среднее число экстремальных точек за единицу пути.

Преобладающими среди неустановившихся режимов движения грузовых автомобилей общего назначения являются трогания и разгоны с переключением передач (рис. 5.6). В этом случае

расчет реализации крутящего момента может быть выполнен по формуле (для двухмассовой колебательной системы)

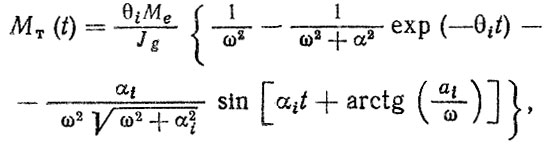
где M_Τ(t) - крутящий момент при трогании, приведенный к первичному валу; θ_i - коэффициенты, отражающие степень использования крутящего момента двигателя М_e; α_i - коэффициенты, зависящие от темпа включения сцепления, c^-1; ω - собственная частота, c^-1; J_д - момент инерции маховика двигателя и приведенных к нему деталей.

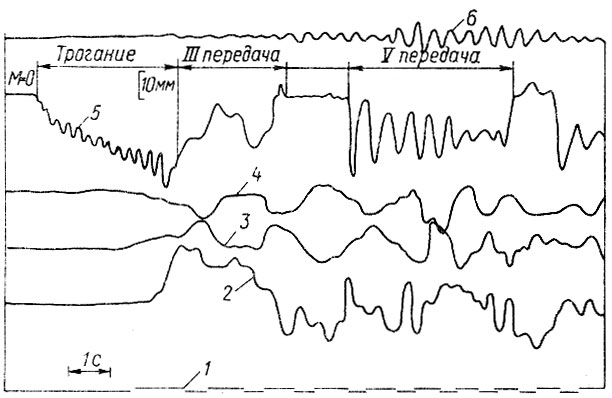
Рис. 5.6. Осциллограмма процесса трогания и разгона с переключением передач автомобиля КамАЭ-53212 с прицепом (Q_Σ = 26,8 т) на грунтовой дороге: 1 обороты переднего колеса; 2-4 - вертикальные перемещения переднего (прогиб рессоры., k = 0,164 см/мм); заднего (k = 0,202 см/мм) и среднего (k = 0,23 см/мм) мостов соответственно; 5 - крутящий момент на полуоси заднего моста (k = 160 Н⋅м/мм); 6 - вертикальное ускорение кузова (k = 0,1 м/с мм)

Схематизация процессов М_Τ(i) позволяет определить f^H_ik(М) и f^0H_ik(M).

При установившихся режимах движения нагрузочный режим трансмиссии определяется, как правило, микропрофилем дороги [41, 77]. Анализ осциллограмм крутящих моментов на валах трансмиссий автомобилей с колесной формулой 4×2 (ЗИЛ-ММЗ-555, ЗИЛ-130, автобусов ЛАЗ), 6×4 и 6×6 (КамАЗ-5320, ЗИЛ-131) показал.

1. Низкочастотные колебательные процессы в трансмиссии могут быть двух видов - линейные и нелинейные (рис. 5.7). Условная граница между ними определяется с помощью среднего квадратического отклонения σ_M и среднего значения M_ψ крутящего момента; при M_ψ > 3σ_M колебательная система может рассматриваться как линейная, при M_ψ < 3σ_M - как нелинейная; определяется по формуле

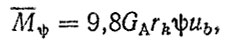(5.34)

где G_A - масса автомобиля, кг; r_k - радиус качения колеса, м; ψ - коэффициент сопротивления движению; u_b - передаточное число трансмиссии от ведущих колес до рассматриваемого вала.

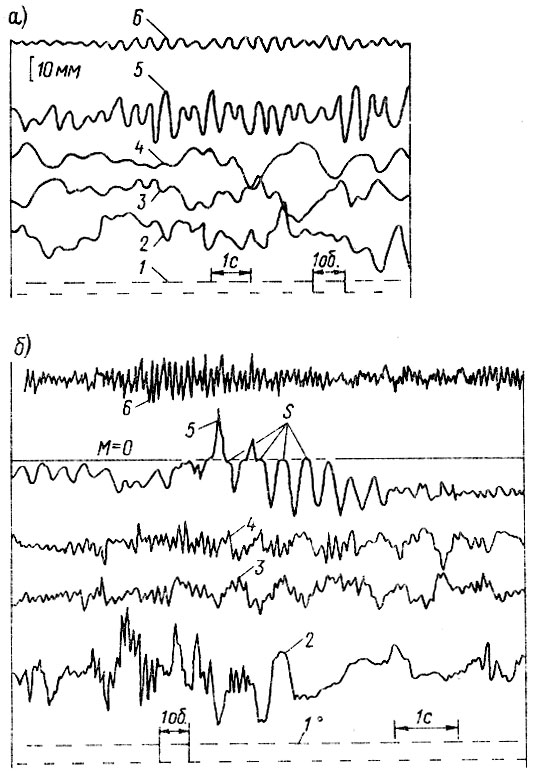
Рис. 5.7. Линейные (а): и нелинейные (б) колебания крутящего момента на полуоси среднего моста 5 (k = 06,5 Н⋅м/мм) груженого (10 т) автомобиля КамАЗ-53212: а - булыжная дорога; 7-я передача, υ_a = 27 км/ч; б - грунтовая дорога, 5-я передача. υ_a = 15 км/ч; S - зазоры в трансмиссии; 1-6 - те же, что м на рис, 5.6

2. Для линейных колебаний расчет σ_M производится с использованием положений статистической динамики линейных систем [77, 80]. Например, на рис, 5.8 приведены четырех- и двухмассовая колебательные системы, эквивалентные трансмиссии и задней подвеске автомобиля. Обозначения элементов на рис. 5,8 следующие: моменты инерции вращающихся частей двигателя I_Д, ведущего моста I_М, колес I_К и поступательно движущейся массы автомобиля I_а; подрессоренная М и не подрессоренная m массы; жесткости валов трансмиссии С_Τ, шин тангенциальная С^Τ_Ш и радиальная С_ш, рессор тангенциальная С^υ_р и изгибная С_р; неупругие сопротивления трансмиссии k_т, рессор k_p и шин k_ш. С учетом двух "входов" - динамического прогиба шины и угловых колебаний картера ведущего моста - спектральная плотность крутящего момента S_M (ω), приведенного к первичному валу коробки передач, определяется по формуле (при I_м = I_k = 0)

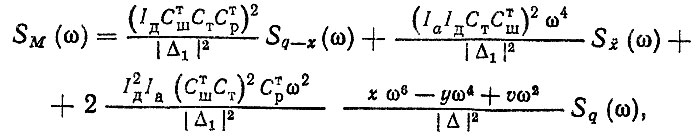(5.35)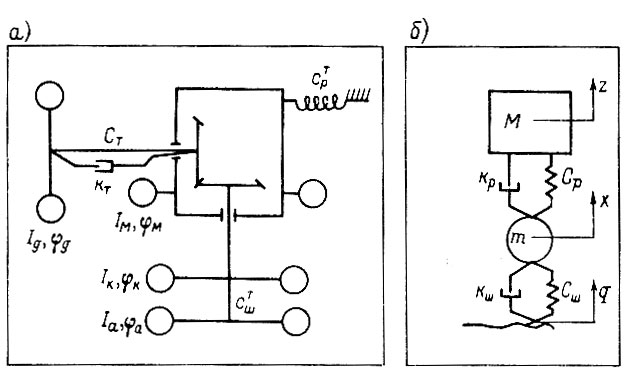

Рис. 5.8. Колебательные системы, эквивалентные трансмиссии (а) и подвеске (б) автомобиля с колесной формулой 4×2

где S_q (ω), S_q-x(ω), S_ẍ(ω) - соответственно спектральные плотности микропрофиля дороги, динамического прогиба шины и вертикальных ускорений ведущего моста;

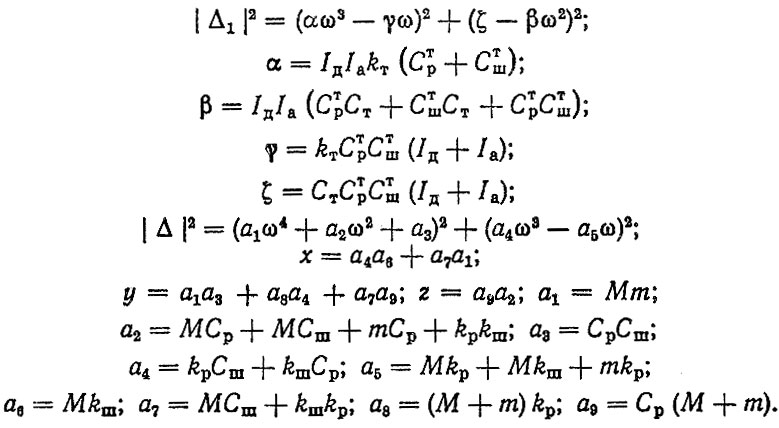
3. Для нелинейных колебаний, основным источником которых являются зазоры в трансмиссии, расчет может быть выполнен двумя способами. Первый способ (численный) включает моделирование процесса движения автомобиля по дороге, ординаты микропрофилей которой воспроизводятся в виде дискретной стационарной последовательности по корреляционной функции; колебательные системы трансмиссии и подвески описываются с помощью системы дифференциальных уравнений, при этом колебательная система трансмиссии включает существенно нелинейный элемент - зазор; решение производится численными методами на ЭВМ; расчетная реализация крутящего момента в трансмиссии подвергается схематизации с помощью известных методов.

Второй способ (аналитический) основывается на методе статистической линеаризации, при этом "вход" в колебательную систему "трансмиссия - подвеска" задается спектральной плотностью микропрофиля дороги, а оценка крутящего момента производится в виде спектральной плотности S_ω(М), по которой определяются σ_M, f^У_iM(М) и т. п. Следует заметить, что Немцову В. В. при использовании первого способа удалось получить хорошее совпадение расчетных и экспериментальных значений динамических нагрузок в трансмиссии полно-приводного автомобиля 4×4"

При использований методов статистической динамики или моделирования процессов движения автомобиля на k-й передаче и на i-м типе дороги оценки нагрузочного режима соответствуют постоянной скорости движения автомобиля υ и загрузке в кузове Q, т. е. элементарному нагрузочному режиму f_ikυQ (М). Для перехода к f_ik (М) с учетом случайных величин скоростей движения υ и загрузки Q вычисления выполняются непосредственно с использованием формулы

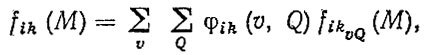(5.36)

где _ik (υ, Q) - двумерная плотность распределения (корреляционная таблица) скоростей движения и загрузки автомобиля.

Аналитический путь расчета предусматривает два варианта. Первый вариант соответствует случаю, когда параметры нагрузочного режима γ_l находятся при υ_i, Q_j = const. После определения коэффициентов a_ijl множественного корреляционного уравнения

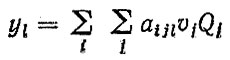(5.37)

рассчитывается плотность распределения f_ik (y_l) параметра y_l

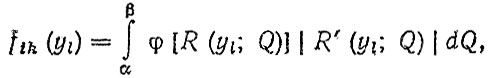(5.38)

где φ ( ) - двумерная плотность распределения случайных величин υ и Q; R (y_l; Q) - функция, обратная (5.37).

Среднее значение y_i и дисперсия σ²_yl параметра y_l находятся по f_ik (y_l). Для расчета ресурса с использованием метода линеаризации рассчитывается также матрица коэффициентов корреляции r_ij параметров y_i и y_j.

Отметим, что в случае, когда (5.43) записывается в виде

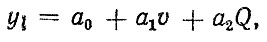
а независимые плотности распределения f(u) и f(Q) подчиняются

нормальным законам распределения, интеграл (5.38) сводится к интегралу Эйлера - Пуассона, т. е.

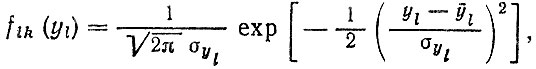(5.39)

где

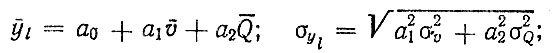
υ, Q - средние значения скорости и загрузки; σ_υ, σ_Q - средние квадратические отклонения.

Второй вариант основан на том, что для некоторых элементов автомобиля среднее значение нагрузочного режима S и коэффициент узко-полостности ε остаются практически постоянными при изменении загрузки Q и скорости υ, тогда как дисперсия σ²_s зависит от υ. Следовательно, плотность распределения нагрузочного режима - стационарного нормального случайного процесса - может быть представлена как условная плотность распределения f_i (S/σ²_s). В этом случае формулы (5.37), (5.38) упрощаются, так как σ²_s зависит только от υ, и расчет плотности распределения f_i (S) на i-м дорожном покрытии производится по формуле

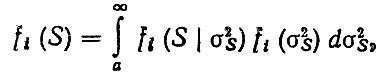(5.40)

где f_i (σ²_s) - плотность распределения σ²_s, определенная с учетом зависимости σ²_s = ψ(υ) и плотности распределения f_i(υ).

В зависимости от в расчет по формуле (5.40) производится для следующих частных случаев. При использовании расчетной величины ε f_i(S|σ²_s) подчиняется распределению Райса (нижний предел а = -∞); при ε = 0 f_i (S|σ²_s) подчиняется распределению Рэлея (а = 0); при ε = 1 f_i<(S|σ>²_s) подчиняется нормальному закону (а = -∞).

Основной способ расчета по формуле (5.46) - численное интегрирование. Однако при описании f_i (σ²_s) двух параметрическим распределением χ² с параметрами k, р и при использовании для f_i (S|σ²_s) распределения Рэлея, f_i (S) определяется по формуле [67].

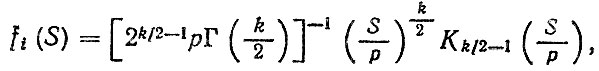(5.41)

где Γ ( ) - гамма-функция; Κ_k/2-1 (S/p) - модифицированная функция Бесселя (функция Макдональда), значения которой табулированы.

Таким образом, обобщенные нагрузочные режимы позволяют объединить результаты экспериментальных (тензометрических) исследований или расчетов, основанных на колебательных системах, эквивалентных агрегатам автомобиля, с данными режимометрических испытаний и рассчитывать долговечность деталей для нормированных (на стадии проектирования) либо заданных условий, в которых эксплуатируются (испытываются) подконтрольные группы автомобилей. Необходимо подчеркнуть, что при расчете обобщенных нагрузочных режимов предполагается равномерное распределение (перемешивание) различных типов дорог, загрузки и т. д. за весь срок службы (пробег) автомобиля. Если в эксплуатации имеется несколько этапов, например, на пробеге 0, ..., L₁ автомобиль используется на междугородних перевозках, на пробеге L₁ ..., L₂ - в условиях города и т. п., то последовательное применение обобщенных нагрузочных режимов для отдельных этапов необходимо дополнить оценками накопленного повреждения, с помощью которых должны формироваться начальные условия для последующего этапа.

Отметим, что понятия обобщенных нагрузочных режимов могут быть использованы и при расчетах на износ. При определении кривой износа по результатам замеров на пробеге до отказа (или капитального ремонта) параметры кривой будут являться обобщенными для данных условий эксплуатации. Для линейных зависимостей износа от пробега, например, в i-x дорожных условиях, суммарная кривая износа запишется в виде

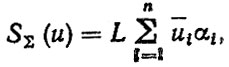(5.42)

где u_i - интенсивность износа в i-х дорожных условиях.

Очевидно, интенсивность износа u_i является тем удельным показателем, с помощью которого формируется обобщенная кривая износа.

Для нелинейных зависимостей, в частности степенной (1.4), уравнение обобщенной кривой износа следующее:

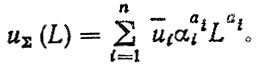(5.43)

Допустим, что u₁ = 0,05, u₂ = 0,01, a₁ = 2, a₂ = 3, α₁ = 0,8, α₂ = 0,2, C_n = 300 мкм. Тогда находим L = 47 тыс. км.