Информация

Современный человек живет в бушующем океане информации. На него обрушивается поток газет, журналов, книг. Электромагнитные волны сотен радио- и телевизионных станций торопятся доставить ему со скоростью света разнообразные сведения. Два миллиона научных работников сидят у приборов, чтобы добыть новые знания об устройстве мира и сообщить их людям. Если в 1800 году во всем мире выпускалось около 100 научных журналов, то теперь их выходит около 100 000. Значит, не зря сидят ученые у приборов и ведут исследования, им есть чем поделиться с современниками.

Чтобы справиться с таким обилием информации, в 40-х годах была создана специальная наука - теория информации. Она изучает закономерности, связанные с передачей, приемом и обработкой информации. Ее основоположником считается выдающийся американский математик и инженер Клод Шеннон.

Всякая теория начинается с уточнения используемых ею слов или терминов. С уточнения смысла слова "информация" началась и новая наука. Смысл этого термина лучше всего можно пояснить, если связать его с другим знакомым словом "неопределенность".

О неопределенности говорят, когда рассматриваемая ситуация может иметь несколько исходов. С ней мы встречаемся перед диагностированием механизма, поскольку для него возможно несколько состояний, а в каком из них механизм находится, мы не знаем. Снять эту неопределенность, указать из множества возможных состояний одно, в котором в действительности находится механизм,- это и составляет задачу диагностики.

Неопределенность - это то же самое, что недостаток информации. Чем больше неопределенность ситуации, тем больше информации о ней недостает. И наоборот, с получением информации неопределенность уменьшается.

Мы указали на связь неопределенности с информацией, но как их оценить числом? Язык инженера - это язык формул. До тех пор, пока научному понятию не найдена количественная оценка, его нельзя использовать для построения теории.

Рассмотрим в качестве примера неопределенности результат падения подброшенной монеты. Возможны два исхода: монета может упасть вверх гербом или решкой. Если начнем угадывать заранее результат ее падения и после многих подбрасываний подведем итоги, то окажется, что примерно в половине случаев мы предсказали результат правильно и в половине случаев - ошиблись.

Будем подбрасывать одновременно четыре монеты. При каждом броске теперь возможны 16 исходов: первая монета упадет вверх гербом, а три остальные - решкой, вторая - вверх гербом, а остальные - решкой и т. д. Если обозначить выпадение герба 0, а решки - 1, то все 16 исходов одного бросания четырех монет можно изобразить так:

Предсказание результата такого бросания оправдается только в одном из 16 случаев.

Очевидно, что неопределенность результата при бросании четырех монет больше, чем при бросании одной монеты. За меру неопределенности ситуации можно было бы взять число n ее возможных исходов. В первом случае n = 2, во втором n = 16. Но по ряду причин, в которые мы здесь вдаваться не будем, неопределенность H оказалось удобнее оценивать логарифмом по основанию 2 от числа возможных исходов:

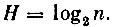
При бросании одной монеты неопределенность равна 1:

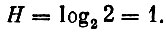
Такая величина неопределенности служит единицей измерения и называется битом^*.

^* (Bit (binary digit) - двоичный разряд.)

Неопределенность результата бросания четырех монет равна 4:

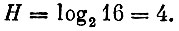
Неопределенность состояния машины перед постановкой ей диагноза зависит от количества отсутствующей информации, необходимой для решения стоящей задачи. Пусть нам нужно знать о состоянии машины только одно, исправна ли она. Здесь два возможных исхода диагноза, поэтому неопределенность равна одному биту, как и при бросании одной монеты. А теперь пусть нам нужно знать, исправен или нет каждый из четырех агрегатов машины - двигатель, трансмиссия, ходовая часть и рулевое управление. При такой постановке задачи диагноза возможны 16 исходов, значит, неопределенность состояния машины равна 4. Если машина состоит из m деталей и о каждой из них нужно знать, исправна она или нет, то возможных состояний машины будет:

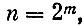
а неопределенность состояния:

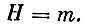
Неопределенность снимается поступлением информации. Поэтому за меру информации, необходимой для устранения неопределенности, можно взять величину неопределенности с обратным знаком. Чем она больше, тем большую информацию должны содержать симптомы, используемые для постановки диагноза машине.

Как же оценить информационную ценность симптома? Пусть у машины различаются n состояний, т. е. неопределенность ее состояния перед диагностированием 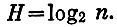При обнаружении у машины некоторого симптома число ее возможных состояний уменьшится, так как некоторые из них несовместны с данным симптомом. Обозначим n₁ - число возможных состояний машины после обнаружения симптома, H₁ - ее неопределенность. Тогда количество информации I, доставляемой этим симптомом, будет равно разности

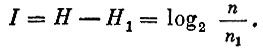
Если после обнаружения симптома состояние машины будет полностью определено, т. е. n₁ = 1, то ее неопределенность станет равной 0, так как log₂ 1 = 0, а количество информации, доставляемой таким симптомом, равно первоначальной неопределенности. Для того чтобы поставить диагноз машине, информация, содержащаяся в используемых симптомах, должна быть не меньше неопределенности состояния машины перед диагностированием.

Говоря о неопределенности, мы несколько упростили вопрос. Дело в том, что неопределенность ситуации зависит не только от числа ее возможных исходов, но и от вероятности их наступления. Неопределенность - это мера случайности исхода рассматриваемой ситуации. Так, если известно, что вероятность застать машину в некотором состоянии равна 0,99, то и без ее диагностирования можно утверждать, что она находится в этом состоянии. При этом мы ошибемся только в одном случае из ста. Значит, здесь неопределенность очень мала. Поэтому для оценки неопределенности существует более сложная формула, чем та, которую приводили выше. Она учитывает упомянутую здесь вероятность состояний:

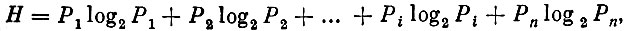
где P_i - вероятность застать машину в состоянии i.

Входящие в формулу вероятности определяются наблюдением за изменением состояния машин подопытной группы. Известно, что одни неисправности появляются чаще, другие реже. В зависимости от частоты появления различных состояний им приписываются соответствующие вероятности. Для примера в таблице указаны вероятности отказа различных элементов трактора, если известно, что он неисправен.

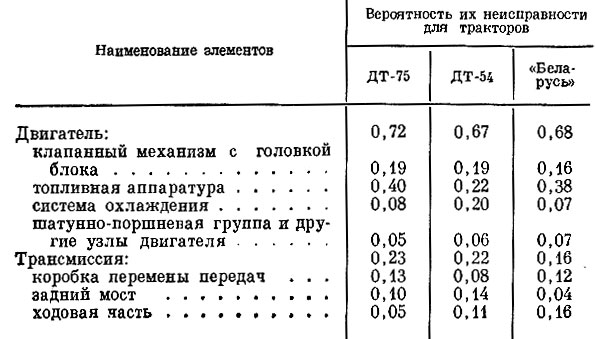
Мы видим, что большинство неисправностей приходится на двигатель, а из элементов двигателя - на топливную систему.

Определим неопределенность состояния трактора ДТ-75:

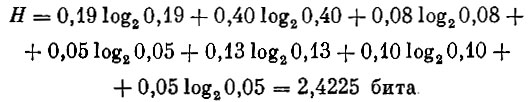
Для облегчения расчетов в книгах по теории информации^* обычно приводятся таблицы величин Plog₂P.

^* (А. М. Яглом и И. М. Яглом. "Вероятность и информация". Гос. изд-во физико-математической литературы. М., 1960.)

Подсчитаем также неопределенность состояния тракторов ДТ-54 и "Беларусь". Они оказываются равными H = 2,6826 бита и H = 2,4665 бита соответственно, т. е. неопределенность состояния трактора ДТ-54 несколько больше, чем других машин, а значит, и его диагноз сложнее. Это объясняется тем, что вероятности отказов распределены по узлам трактора ДТ-54 более равномерно. Поэтому, если обнаружено, что трактор неисправен, то угадать заранее, какой узел виноват в этом, для трактора ДТ-54 труднее, чем для других машин. Например, у трактора ДТ-75 40% поломок приходится на топливную аппаратуру, поэтому, не ставя ему диагноза, можно наугад заявить, что неисправна топливная аппаратура, и в сорока случаях из ста это подтвердится. Такая неравномерность отказов вообще характерна для новой неотработанной конструкции.

Создание теории не является самоцелью. Их разрабатывают для решения практических задач. "Нет ничего более практичного, чем хорошая теория",- сказал в свое время знаменитый немецкий физик Макс Планк. Поэтому, если бы теория информации только и могла делать, что подсчитывать неопределенность, то пользы от нее было бы мало.

Основная практическая задача, для решения которой служит теория информации,- это передача сообщений без искажения.