Сигнал

Доставку информации потребителю обеспечивают сигналы. Сигналом может служить процесс любой физической природы, способный перемещаться на расстояние. В радиосвязи в качестве сигналов используются электромагнитные волны. Они переносят информацию на огромные расстояния с большой скоростью, равной скорости распространения света (300 000 ^км/_сек).

В диагностике сигналами могут служить упругие волны, возбуждаемые в механизме соударениями деталей. Они свободно распространяются по металлу и без труда доставляют информацию из недр машины. В механизмах путь сигнала от посылающей его детали до приемника, расположенного на корпусе, короткий, поэтому не удивительно, что к приемнику приходят "голоса" всех деталей.

Сигнал может переносить информацию благодаря тому, что некоторые его параметры способны изменяться в зависимости от содержания информации. Процесс наполнения сигнала информацией называют кодированием. О кодировании более подробно мы расскажем в следующем параграфе. А сейчас рассмотрим два вида сигналов, с которыми приходится иметь дело в диагностике.

Различают сигналы импульсные и непрерывные. Сигнал, величина которого отлична от нуля только в течение конечного интервала времени, называется импульсным. Между собой такие сигналы отличаются амплитудой А, длительностью m, положением на оси времени относительно начала отсчета t_o и формой. Все эти параметры импульса могут изменяться, а поэтому и переносить информацию.

Для передачи сообщений редко используются одиночные импульсы. Обычно импульсный сигнал представляет собой последовательность импульсов, возникающих один за другим. Таким сигналом, например, будут соударения деталей в работающей кинематической паре. При движении механизма удары деталей в кинематической паре повторяются через определенные интервалы времени.

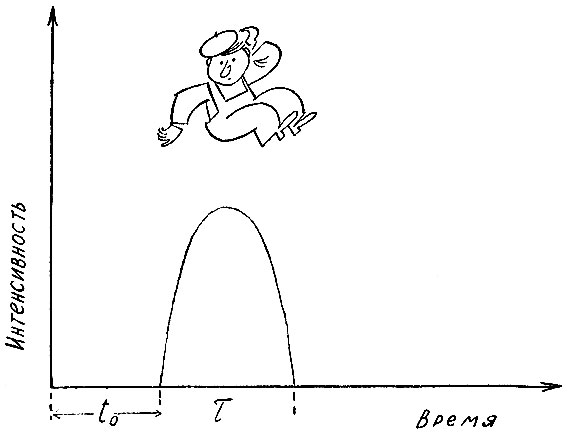
Рис. 4 Импульс

Вместе с импульсным почти всегда передается опорный сигнал. Им задается шкала отсчета времени, поэтому иногда его называют тактирующим сигналом. Опорный сигнал представляет собой периодическую последовательность импульсов произвольной формы и амплитуды. Интервал времени T (период) между импульсами опорного сигнала постоянен. В результате смещения импульсов основного сигнала относительно опорных происходит передача информации.

В диагностике для выработки опорного сигнала выбирают какую-либо характерную фазу движения механизма и устанавливают на механизм специальный датчик для ее регистрации. Так, в двигателях внутреннего сгорания за начало отсчета времени принимают момент, в который поршень одного из цилиндров проходит верхнюю мертвую точку (в. м. т.). Для регистрации этого момента в соответствующем месте маховика просверливают отверстие или наносят риску. Датчик, установленный на картере маховика, регистрирует момент прохождения мимо него отверстия или риски и вырабатывает в этот момент импульс, который служит опорным сигналом и синхронизует работу всех блоков диагностической аппаратуры. По величине смещения импульсов, возбуждаемых ударами клапанов, иглой форсунки и другими элементами двигателя относительно опорного импульса, можно оценить степень их разрегулировки.

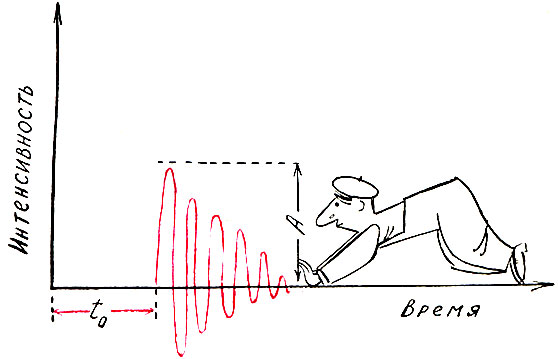
Рис. 5. Импульс с высокочастотным заполнением

Непрерывный сигнал равен нулю только в некоторые моменты времени, а все остальное время отличен от нуля. В нем различают высокочастотное заполнение и его огибающую. В радиотехнике высокочастотное заполнение называют также несущей. Она представляет собой очень быстрое колебание - миллионы циклов в секунду. Сигналы, передаваемые различными радиостанциями, отличаются частотой колебаний несущей, это и позволяет радиоприемнику принимать сигнал только нужной станции. Огибающая радиосигнала имеет сравнительно низкую частоту - от нескольких десятков до нескольких тысяч колебаний в секунду. Ее изменение происходит в такт передаваемого сообщения, т. е. ее форма соответствует колебаниям мембраны микрофона при восприятии речи диктора или музыки. Собственно говоря, информация, переносимая радиосигналом, содержится только в его огибающей. Поэтому, чтобы ее воспроизвести, в радиоприемнике имеется специальное устройство - детектор, который выделяет огибающую радиосигнала и направляет ее в громкоговоритель. Эффективность передачи сообщения существенно зависит от глубины модуляции. Грубо говоря, глубина модуляции колебаний - это разность между горбом и впадиной огибающей, отнесенная к величине горба.

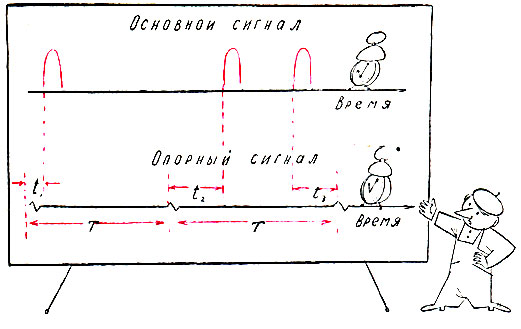
Рис. 6. Последовательность импульсов и опорный сигнал

Мы подробно остановились на радиосигнале потому, что он имеет много общего с сигналом, используемым в диагностике. Здесь также имеется высокочастотное заполнение (несущая) и огибающая. Заполнение, как и в радиотехнике, используется для выделения нужной "станции", которой здесь являются кинематические пары, посылающие сигналы. Но в отличие от радиосигналов, несущая которых представляет простое синусоидальное колебание, в диагностике несущая образуется как смесь очень многих синусоидальных колебаний разных частот. Основная информация диагностического сигнала также содержится в его огибающей, поэтому диагностические приборы почти всегда имеют детектор, который позволяет отделить огибающую от несущей. Эффективность диагностики очень существенно зависит от глубины модуляции сигнала, поэтому позже мы уделим этому вопросу определенное внимание.

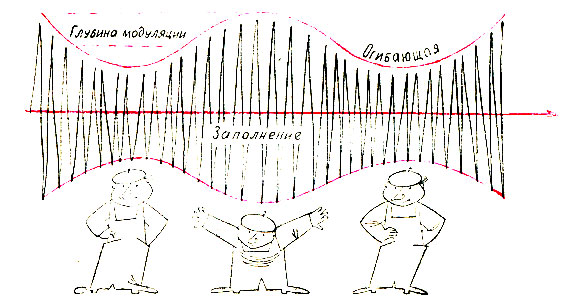
Рис. 7. Непрерывный сигнал

Многообразие сигналов, используемых для передачи сообщений, не поддается перечислению. Мы рассмотрим только два, которые считаются элементарными, так как из них можно построить сигнал любой формы. Один из этих сигналов будет импульсным, другой - непрерывным.

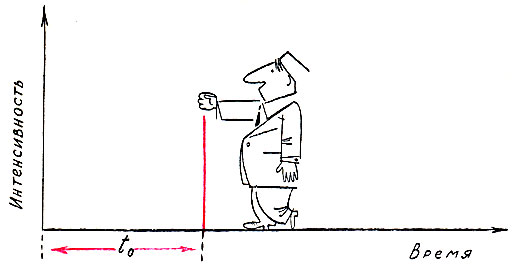
Рис. 8. Дельта-импульс

Представьте очень короткий импульс, длительностью которого можно пренебречь, но площадь которого имеет конечную величину q₀. Чтобы удовлетворить такие требования, мы должны принять, что амплитуда нашего импульса бесконечно велика. Очевидно, что в природе такие импульсы не встречаются. Даже самые быстротечные процессы имеют конечную длительность. Так, соударение деталей продолжается всего пятьдесят - сто миллионных долей секунды, но все же это время больше нуля.

Не встречаются в природе и бесконечно большие интенсивности. В момент удара деталей в зоне их контакта возникает огромное давление, измеряемое тысячами атмосфер, но оно имеет конечную величину. И тем не менее мы рассмотрим такой идеализированный импульс. Идеализация вообще является основным методическим приемом науки. Наука рассматривает, как правило, искусственные схематизированные объекты с очень прозрачной структурой. Именно на них удобнее всего решать принципиальные вопросы. Познание - сложный и многогранный процесс отражения действительности. Он развивается согласно ленинской формулировке "от живого созерцания к абстрактному мышлению и от него к практике".

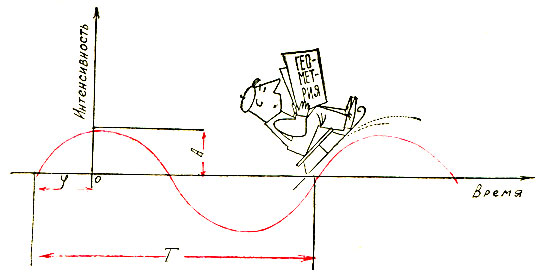
Рис. 9. Синусоида

Если площадь, ограниченная рассматриваемым импульсом равна q₀ = 1, то такой импульс называют дельта-импульсом Дирака, по имени знаменитого английского физика. У дельта-импульса имеется только один параметр, который способен изменяться, а значит, и переносить информацию. Это момент времени t, в который возникает импульс. В дельта-импульс можно ввести еще один переменный параметр q₀, соответствующий его интенсивности.

Другим элементарным и тоже идеализированным сигналом будет синусоидальный процесс:

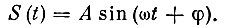
Форму этого сигнала можно получить, если закрепить на конце маятника перо, заставить его колебаться и перпендикулярно плоскости колебаний с постоянной скоростью протащить бумажную ленту. Перо нарисует на бумаге синусоиду.

Величина А в формуле характеризует размах колебаний, она называется амплитудой, ω - частота колебаний, измеряемая числом радиан в секунду. Эта частота называется круговой и используется только для упрощения формул. Обычно частоту колебаний измеряют в натуральных единицах, числом полных колебаний в секунду. Одно колебание в секунду называют герцем. Герц служит обычно единицей измерения частоты. Частоту колебаний, выраженную в герцах, мы будем обозначать v. Для перехода от круговой частоты к натуральным единицам можно использовать следующую формулу:

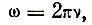
где π = 3,14...

Величина φ называется начальной фазой. Она определяется положением начала отсчета времени.

В естественных науках существуют два основных методических подхода к изучению различных явлений: временной и спектральный. В первом случае интересуются развитием процесса во времени. Примером временной картины является осциллограмма колебаний механизма, зарегистрированная датчиком. На ней мы видим моменты времени, в которые амплитуда колебаний имеет максимальную и минимальную величины, видим изменение огибающей, т. е. весь ход процесса.

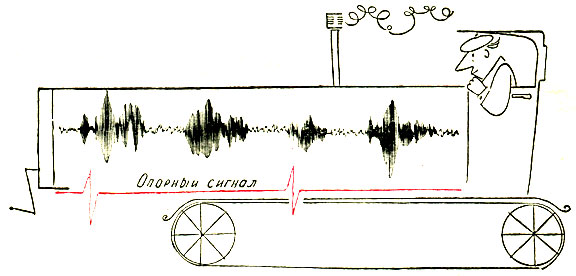
Рис. 10. Осцилограмма колебаний двигателя

При спектральном подходе процесс рассматривается как набор синусоидальных колебаний. Этот набор называют спектром процесса. Его можно изобразить графически. Каждая синусоидальная составляющая изображается вертикальной линией. Положение этой спектральной линии указывает частоту колебаний синусоиды, а высота - амплитуду. На спектре процесса можно видеть, какие синусоиды входят в его состав и какова их интенсивность. При спектральном рассмотрении один процесс отличается от другого частотой образующих его синусоид и их интенсивностью. Многие процессы, в частности импульсы, а также акустический сигнал механизмов, имеют спектр, линии которого сливаются. Такой спектр называется сплошным. Он показывает, что процесс образован бесконечно большим числом синусоид, частоты которых непрерывно заполняют определенный частотный диапазон.

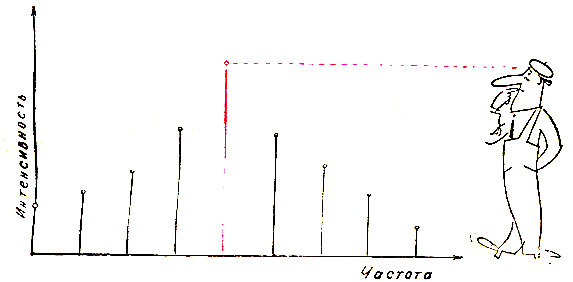
Рис. 11. Положение спектральных линий указывает частоту синусоид, входящих в состав сигнала, их высота - интенсивность составляющих

Кроме указанных спектров, которые называются амплитудными, каждый процесс имеет также спектр фаз. Но с ним нам в дальнейшем встретиться не придется, поэтому мы его рассматривать не будем.

Разложение процесса на синусоидальные составляющие называется спектральным анализом. Для его осуществления имеются специальные приборы - спектральные анализаторы. Они устроены так, что если на их вход подать какой-либо процесс, например колебание механизма, то на выход они пропускают из всего процесса только одну представляющую определенный интерес синусоиду или несколько синусоид с близкими частотами, так что можно измерить их интенсивность.

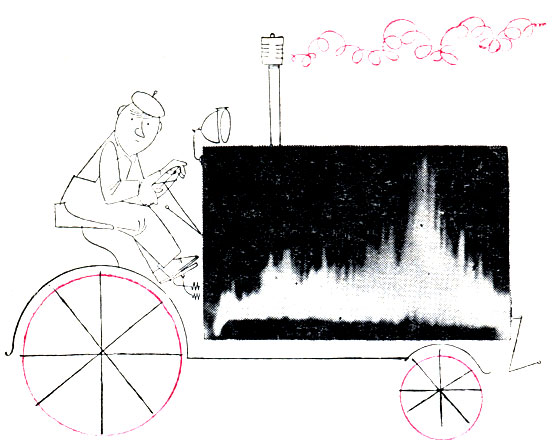
Рис. 12. Спектр колебаний двигателя непрерывный, то есть указывает на то, что в состав сигнала входят синусоиды всех частот. Такой спектр имеют одиночные импульсы и случайные сигналы (шумы)

Оба подхода к изучению явлений, временной и спектральный, равноправны. Существуют методы, которые называются преобразованиями Фурье, позволяющие по развитию процесса во времени определить его спектр и, наоборот, по спектру восстановить картину протекания процесса. Но каждый из этих подходов обладает спецификой и наиболее удобен для отражения определенных свойств изучаемого явления.

При решении проблем передачи, приема и преобразования информации преобладает спектральный подход. Чаще рассматривают не изменение сигнала во времени, а его спектр. Поскольку проблема диагностики - это проблема получения информации, то очень многие вопросы приходится обсуждать, пользуясь спектральным языком.

С чем связана необходимость использования спектров вместо рассмотрения изменений сигналов во времени? Методические преимущества спектрального подхода состоят в основном в том, что, разложив сигнал на элементарные части (синусоиды), мы можем проследить за всеми его преобразованиями, изучая преобразования каждой синусоиды в отдельности. При передаче сигнала по каналу связи каждая его синусоидальная составляющая проходит независимо от других. Правда, это наблюдается только в так называемых линейных каналах, но многие реальные каналы можно считать линейными. Преимущество спектрального подхода состоит еще и в том, что синусоида обладает замечательным свойством - форма ее не меняется при прохождении по большинству каналов. Ниже мы часто будем пользоваться спектрами и по ходу изложения давать дополнительные пояснения.