Модуляция акустического сигнала

Распространение волн в среде связано с колебанием ее частиц, поэтому напомним некоторые свойства колебательного движения. Это удобно сделать на примере простейшей колебательной системы - грузика с прикрепленными к нему двумя пружинами.

В положении равновесия на грузик с противоположных сторон действуют одинаковые силы, направленные в разные стороны. Если грузик сместить из этого положения, то давление на него одной пружины увеличится, а другой ослабнет. В результате силы будут стремиться вернуть грузик в положение равновесия. Но если его отпустить, то он не остановится в положении равновесия, а по инерции проскочит эту точку и отклонится в другую сторону. Тогда равновесие нарушится в другом положении грузика и возникнут колебания.

Колебания, которые начнет совершать грузик, выведенный из положения равновесия, называются синусоидальными или гармоническими, а система, способная совершать такие колебания,- гармоническим осциллятором. Рассмотрение свойств осциллятора играет большую роль в учении о колебаниях. Это связано с тем, что движение любой сложной системы можно представить, как колебание определенного набора гармонических осцилляторов. В акустической диагностике моделью механизма служит набор осцилляторов, а акустический сигнал рассматривается, как сумма их колебаний.

Мы начнем изучение колебаний механизма, считая его простым гармоническим осциллятором. Рассмотрим его движение после возбуждения ударом деталей. Колебание осциллятора после удара будет происходить по закону синусоиды:

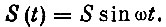
Здесь S обозначает амплитуду (размах) колебаний, ω - их частоту.

Теория колебаний доказывает, что частота колебаний осциллятора при возбуждении его ударом не зависит от характера удара, а целиком определяется свойствами осциллятора, массой грузика и жесткостью пружин. Поэтому она называется собственной частотой осциллятора. Амплитуда колебаний, очевидно, зависит от интенсивности Удара: чем он сильнее, тем больше размах колебаний.

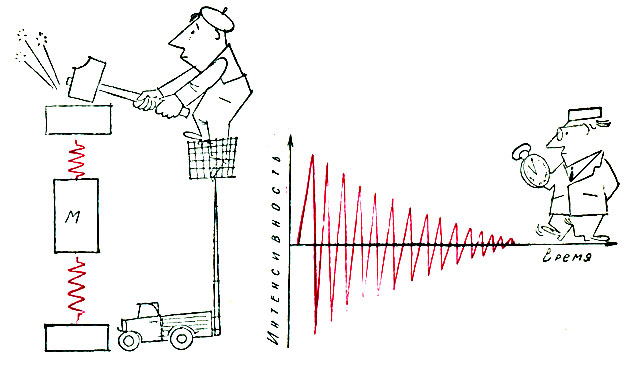
Рис. 26. Первоначальная амплитуда колебаний осциллятора после удара зависит от интенсивности удара, а скорость ее уменьшения - от величины коэффициента затухания

Интенсивность удара в механике оценивают величиной импульса силы mv₀. В нашем случае m равно приведенной массе сталкивающихся деталей, а v₀ - скорости их соударения.

Амплитуда колебаний осциллятора определяется следующей формулой:

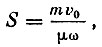
где μ - масса грузика осциллятора.

Мы показали раньше, что скорость соударения деталей зависит от состояния кинематической пары, например от зазора в ней. Поэтому амплитуда осциллятора будет зависеть от состояния пары, возбудившей его колебания. Измеряя амплитуду сигнала, можно оценить состояние пары.

При рассмотрении движения осциллятора мы допустили неточность, пренебрегая трением. Поэтому приведенная выше формула колебаний представляет дело так, как будто после удара осциллятор продолжает совершать синусоидальные колебания вечно. В действительности же всякое колебание со временем затухает. Чтобы отразить этот факт, в формулу синусоиды нужно ввести дополнительный множитель 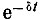и записать ее в следующем виде:

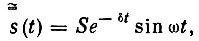
где δ - коэффициент затухания. Чем больше его величина, тем быстрее уменьшается амплитуда колебаний от одного размаха к другому.

Необходимо ввести еще одно уточнение. Дело в том, что удары в кинематических парах во время работы механизма повторяются. Поэтому посмотрим, как движется осциллятор при воздействии на него не одним, а серией повторяющихся ударов. Будем считать, что соударения в кинематической паре происходят редко, т. е. между двумя ударами осциллятор успевает совершить большое число колебаний. Именно этот Случай наблюдается в механизмах, где частота колебаний осцилляторов равна нескольким тысячам герц, а удары деталей происходят с частотой в несколько десятков герц.

Колебания осциллятора при периодическом воздействии ударов будут иметь характерный вид, изображенный на рисунке. Непосредственно после удара их амплитуда имеет наибольшую величину, но затем она постепенно уменьшается и принимает наименьшее значение в момент, предшествующий очередному удару. Колебание с изменяющейся амплитудой называют модулированным, а изменение амплитуды - огибающей. Информация об ударах, а значит, и о состоянии кинематической пары содержится только в огибающей сигнала. Здесь положение точно такое же, как в радиотехнике. Высокочастотное синусоидальное колебание (несущая) там служит только признаком действия радиостанции, который позволяет настроиться на ее волну. Вся же информация (речь диктора, музыка) заключена в огибающей радиосигнала. Поэтому, прежде чем по-дать радиосигнал в репродуктор, его детектируют. Эта операция состоит в том, что огибающую сигнала отделяют от несущей. В диагностике сигнал, полученный датчиком, также пропускают через детектор и диагноз кинематической паре ставят на основании измерения параметров огибающей.

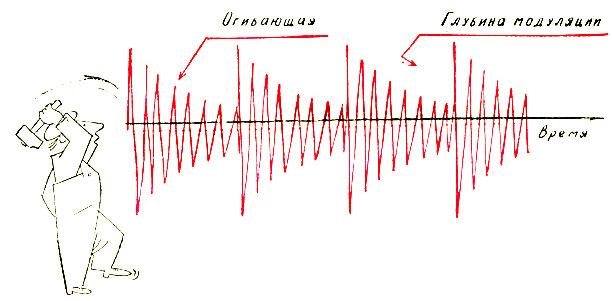
Рис. 27. Колебания осциллятора при возбуждении его серией ударов

При прочих равных условиях точность любого измерения тем выше, чем сильнее сигнал. Интенсивность огибающей зависит от разности максимальной и минимальной амплитуд колебаний Для характеристики огибающей вводится специальный показатель - коэффициент глубины модуляции R.

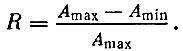
Чем больше глубина модуляции колебаний, тем легче поставить диагноз кинематической паре, которая их возбудила. Глубина модуляции зависит от частоты следования ударов. Чем реже они происходят, тем на большую величину успевают затухнуть колебания до очередного удара. В свою очередь, частота ударов зависит от скоростного режима механизма. Чем меньше его скорость, тем реже происходят удары в кинематических парах. Отсюда следует практическая рекомендация производить диагностику механизма на минимально возможном скоростном режиме. Тогда глубина модуляции акустического сигнала будет наибольшей.

Глубина модуляции акустического сигнала зависит также от коэффициента затухания δ. Затухание колебаний в механизмах происходит потому, что их энергия расходуется на некоторые другие процессы: на нагрев материала механизма и на излучение колебаний в окружающую среду. Опыт показывает, что затухание колебаний тем больше, чем выше их частота. Поэтому для увеличения глубины модуляции следует выбирать в качестве сигнала колебание того осциллятора, у которого частота наибольшая.