Акустический сигнал

Задача науки - получение новых знаний. Но наука - это не просто знания каких-то фактов, а прежде всего система знаний, которая оформляется в виде теорий. В теории находят отражение количественные соотношения между различными факторами, характеризующими рассматриваемое явление. Но теория - не зеркальное отражение действительности. Она освещает только те ее стороны, которые с точки зрения решаемой задачи считаются существенными. Упрощая ситуацию, теория позволяет обнажить основные рычаги, движущие развитием событий, сделать прозрачной структуру явления.

Любая теория строится из трех конструктивных элементов: системы понятий, исходных утверждений и следствий. Система понятий - это язык, на котором теория описывает явление. В отличие от обыденных слов, значения которых часто многозначны, научным понятиям придается точный смысл.

Наша задача - дать теорию спектра акустического сигнала механизма. Основным понятием будет понятие об акустическом канале механизма. О канале связи, как о системе, по которой передаются сигналы, мы уже говорили, поэтому ограничимся только уточнением этого понятия применительно к рассматриваемому кругу вопросов.

Акустическим каналом в механизме будем называть систему, состоящую из кинематической пары, датчика колебаний, установленного на корпусе механизма, и среды, по которой сигнал от кинематической пары передается к датчику. Сигнал, вырабатываемый кинематической парой и представляющий собой последовательность соударений де-талей, будем называть входным сигналом, а сигнал, регистрируемый датчиком,- выходным. Наша задача состоит в том, чтобы объяснить форму спектра выходного сигнала. Очевидно, что в механизме насчитывается столько акустических каналов, сколько в нем кинематических пар. Это и позволяет нам считать механизм многоканальной системой связи.

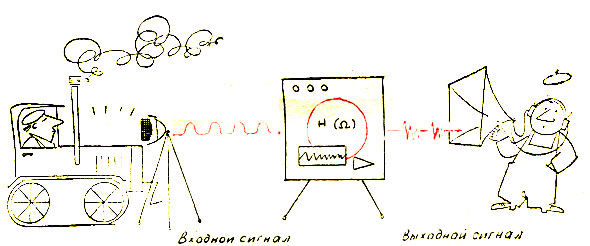
Рис. 28. Акустический канал. На вход поступает последовательность импульсов соударения деталей. На выходе датчик регистрирует колебания, возбуждаемые этими импульсами

Второй элемент, без которого не обходится ни одна теория,- это исходные утверждения. Они бывают двух видов: допущения и утверждения других теорий. Допущения являются своеобразным и необходимым элементом любой теории. Их своеобразие состоит в том, что они всегда противоречат действительности, но оспаривать их правомочность не имеет смысла до тех пор, пока не будут проверены результаты самой теории, основу которой они составляют. "Будем считать солнце и планеты точками, не имеющими размеров",- говорит астроном и, пользуясь этим допущением, предсказывает положение планет и солнечные затмения на много лет вперед с точностью до малых долей секунды. "Полезная ложь лучше бесполезной правды",- утверждает народная мудрость, и само существование науки подтверждает это, потому что наука и шага не может ступить, не пользуясь допущениями. Конечно, мы знаем, что и солнце и планеты - не точки, а огромные тела, но если бы мы стали догматически держаться за эту "правду", то никогда не узнали бы законов движения небесных светил.

Основным допущением в теории спектров акустических сигналов служит утверждение о линейности акустического канала. Другими словами, предполагается, что при распространении в механизме упругих волн, возбужденных соударением деталей, материал механизма подчиняется закону Гука: его напряжения пропорциональны возникающим деформациям.

Линейный канал обладает многими замечательными свойствами: сигналы, посылаемые различными парами механизма, проходят по нему независимо один от другого; при прохождении сигнала по каналу в нем никогда не появляются новые частотные составляющие, которых не было у отправленного сигнала; линейный канал не изменяет формы синусоидального сигнала, возможно только увеличение или уменьшение его амплитуды и сдвиг начальной фазы.

Воспользуемся последним свойством линейного канала для вывода основной формулы, которой устанавливается зависимость спектра сигнала, регистрируемого датчиком, от спектра импульса соударения деталей в кинематической паре.

Пусть к детали рассматриваемой кинематической пары приложена переменная сила q(t), меняющаяся по закону синусоиды:

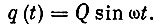
Мы знаем, что взаимодействие деталей в кинематических парах носит импульсный характер, но любой импульс может быть разложен на гармонические составляющие, образующие его спектр, поэтому рассматриваем сейчас одну гармоническую составляющую спектра импульса.

Датчик, находящийся на корпусе механизма, воспримет синусоидальный сигнал, поскольку в линейном канале синусоида не меняет формы:

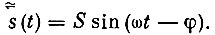
Отношение амплитуды принятого сигнала к амплитуде отправленного

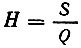
называют коэффициентом усиления канала, так как оно показывает, во сколько раз увеличивается (уменьшается) амплитуда сигнала при передаче его по каналу. Параметр φ характеризует задержку сигнала, т. е. изменение его начальной фазы.

Величины H и φ зависят в общем случае от частоты со передаваемого сигнала. Синусоиды разной частоты могут усиливаться (ослабляться) в канале по-разному. Функция частоты H (ω) называется амплитудной частотной характеристикой канала, а функция φ(ω) - его фазовой характеристикой. Эти характеристики полностью определяют свойства линейного канала. В дальнейшем фазовая характеристика канала нам - не потребуется, поэтому мы будем называть частотной характеристикой канала функцию H(ω), опуская слово амплитудная.

Амплитуда сигнала S, регистрируемого датчиком, равна произведению амплитуды сигнала, отправляемого кинематической парой Q, на коэффициент усиления канала H:

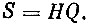
Спектр импульса соударения деталей 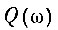- это функция, определяющая величину амплитуды составляющей в зависимости от ее частоты. Он показывает, как меняется амплитуда синусоид, входящих в состав импульса, в зависимости от их частоты. На рисунке мы видим, что амплитуды синусоид уменьшаются с ростом частоты и после значения частоты v_в их интенсивность очень мала. Эту частоту можно принять за верхнюю границу спектра импульса, так как импульс не может возбудить существенные колебания в механизме с частотой выше v_B. То же самое можно сказать и о спектре сигнала 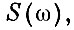регистрируемого датчиком,- это функция амплитуд составляющих выходного сигнала в зависимости от их частоты. Поэтому приведенную выше формулу можно записать так:

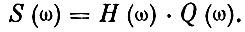
Это замечательный результат, позволяющий определить спектр акустического сигнала, если известен спектр соударения деталей и частотная характеристика канала.

Рис. 29. Спектр импульса соударения деталей

Любое явление природы имеет многочисленные связи с другими явлениями, поэтому в его теории всегда используются результаты других теорий. Фундамент теории спектров акустических сигналов составляют теория Герца о соударении упругих тел и теория излучения точечного источника. О теории Герца мы уже упоминали. Она позволяет определить форму и длительность импульса соударения деталей. Согласно этой теории, импульс имеет форму полуволны косинусоиды:

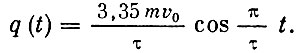
Пользуясь формулами преобразования Фурье, можно найти спектр такого импульса:

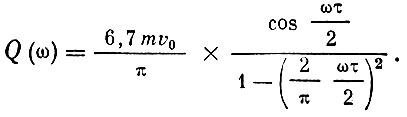
Теорию излучения точечного источника мы здесь изложить не сможем, поскольку понадобилось бы использовать математический аппарат, знакомство с которым не предполагается у читателя данной книги. Но основной вывод приведем и постараемся пояснить его.

В разделе, посвященном рассмотрению колебаний гармонического осциллятора, было показано, что его амплитуда пропорциональна возмущающему импульсу mv₀ и обратно пропорциональна частоте ω. Акустический канал мы будем представлять как набор осцилляторов с всевозможными частотами. Поэтому, если на вход канала подать сигнал, амплитуда составляющих которого одинакова, то амплитуда колебаний осцилляторов будет обратно пропорциональной их собственной частоте.

В акустической диагностике используются датчики, которые регистрируют не смещение массы осцилляторов, а их ускорение. Амплитуда смещения массы осциллятора S и ее ускорение связаны соотношением:

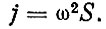
Покажем это. Если смещение массы осциллятора описывается формулой

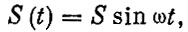
то скорость массы равна производной:

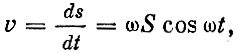
а ускорение равно производной от скорости осциллятора:

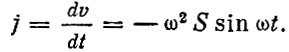
Поэтому если амплитуда смещения массы осцилляторов уменьшается обратно пропорционально их частоте, то ускорение, наоборот, увеличивается пропорционально частоте. Эти рассуждения позволяют нам определить форму частотной характеристики канала, которая показывает, что по мере возрастания частоты составляющих входного сигнала их амплитуда на выходе канала линейно возрастает.

Частотная характеристика акустического канала имеет гребенчатый вид, причем ее зубья (спектральные выбросы) возрастают по мере увеличения частоты. Частотную характеристику реального механизма можно определить, если по одной из деталей кинематической пары нанести очень короткий удар (дельта-импульс) и снять спектр возбужденных при этом колебаний. Этот спектр и будет частотной характеристикой канала.

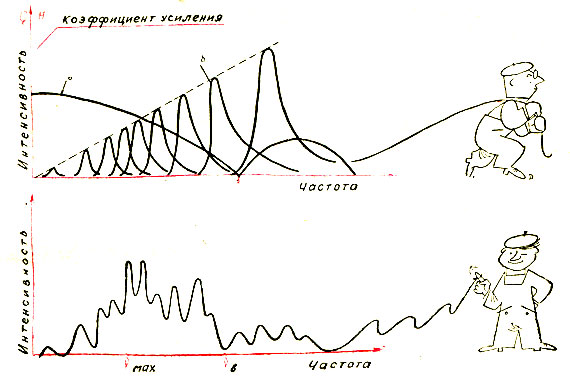
Рис. 30. Перемножение спектра входного сигнала Q (ω) на частотную характеристику канала H(ω)

Зная спектр входного сигнала Q(ω) и частотную характеристику канала H(ω) и перемножив их, легко найти спектр сигнала S(ω), регистрируемого датчиком. Знание спектра нам понадобилось для решения двух практических вопросов: для определения верхней границы спектра v_B и для определения частоты v_max, на которую приходится составляющая с максимальной интенсивностью. Зная верхнюю границу спектров акустических сигналов, мы можем более правильно подойти к выбору рабочего частотного диапазона диагностической аппаратуры. Знание частоты, на которую приходится максимальная интенсивность сигнала, генерируемого данной кинематической парой, позволяет использовать частотную фильтрацию для выделения ее сигнала. Перемножение Q(ω) и H(ω) дает следующие формулы для v_B и v_max:

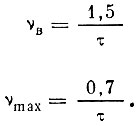
Таким образом, оба параметра спектра зависят от длительности соударения деталей. А поскольку длительность для различных кинематических пар неодинакова, то будут различными и указанные параметры спектров сигналов, генерируемых различными кинематическими парами.

Чтобы закончить рассказ о спектрах, остается указать на одну неточность, которую мы допустили при рассмотрении частотной характеристики механизмов. В упругом теле неограниченных размеров могут возникать колебания любой частоты. Это мы и предполагали, представив акустический канал как набор осцилляторов всевозможных частот. В действительности механизм - упругое тело ограниченных размеров. В таких телах, согласно теории колебаний, могут возбуждаться волны только вполне определенных частот. Поэтому частотные характеристики акустических каналов имеют форму не наклонной прямой линии, а волнообразной кривой, высота гребней которой возрастает с частотой. Ее гребни называют спектральными выбросами или резонансами. Такой вид реальных частотных характеристик несколько усложняет форму спектров сигналов, но не изменяет полученный вывод о зависимости их основных параметров v_B и v_max от длительности удара деталей в кинематической паре.