Усреднение

Любое измерение содержит погрешность. Для повышения точности измерения повторяют несколько раз и результат усредняют. Если одиночное измерение содержит погрешность Δx, то погрешность результата, полученного после п измерений, уменьшается в √n раз. Так утверждает теория измерений.

Все сказанное целиком относится к диагностике. Здесь также не ограничиваются одиночным измерением амплитуды и положения импульса, отправленного кинематической парой. Поскольку кинематическая пара вырабатывает импульсы периодически, то измерительное устройство определяет параметры у серии импульсов и результат усредняет.

Для повышения точности следует увеличивать продолжительность диагноза и, наоборот, если необходимо сократить его время, то придется удовлетвориться меньшей точностью. Здесь существует такая простая зависимость. Обозначим Δx - погрешность измерения амплитуды (или фазы) одиночного импульса, а ε - допустимую погрешность диагноза. Поскольку обе погрешности связаны зависимостью

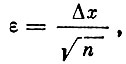
где n - число измерений сигнала, обеспечивающее заданную точность ε, то для получения заданной точности нужно измерить амплитуду (фазу) у n импульсов, где

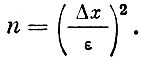
Импульсы вырабатываются кинематической парой с периодом T. Отсюда длительность диагноза 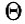следующим образом связана с его точностью:

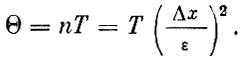
Для повышения точности и особенно надежности диагноза прибегают и к другому способу усреднения. Он состоит в том, что диагноз механизму ставят на разных скоростях и нагрузочных режимах, а затем результаты всех диагнозов согласуют между собой.