7.5. Эксперимент с изменением нескольких параметров

В разделе 5.5 показана ошибочность предположения о том, что изменения выходных данных модели, вызванные одновременными изменениями значений нескольких параметров входа, сводятся к простой сумме изменений, являющихся следствием изменений значения каждого из этих параметров по отдельности. Данные, приведенные в разделе 7.2, свидетельствуют о практически аддитивной связи между результатами экспериментов М и О по отношению к результатам эксперимента N. Для того чтобы строже исследовать зависимости между несколькими входными параметрами, проведен эксперимент, в котором одновременно изменялись значения нескольких параметров, и сравнивались результаты этого эксперимента с вероятными в условиях раздельного варьирования тех же параметров при соблюдении предположения аддитивности. Результаты этого эксперимента показаны на рис. 33, 34, 35, 36 сплошными линиями. Пунктирными линиями представлены ожидаемые результаты при условии независимости и аддитивности параметров.

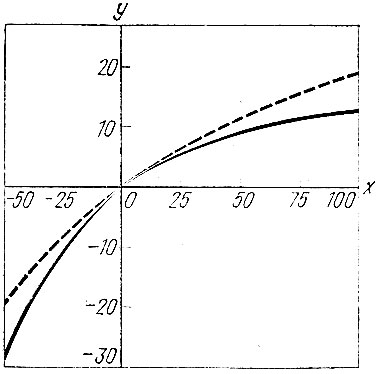
Рис. 33. Многопараметрический эксперимент (изменения в общем числе поездок на индивидуальном транспорте): х - относительное изменение (в %) входных параметров по сравнению с их значением в НВБ; у - изменения (в %) в результате одновременного варьирования входными параметрами (сплошная линия), ожидаемое изменение в предположении его аддитивности по входным параметрам (пунктир)

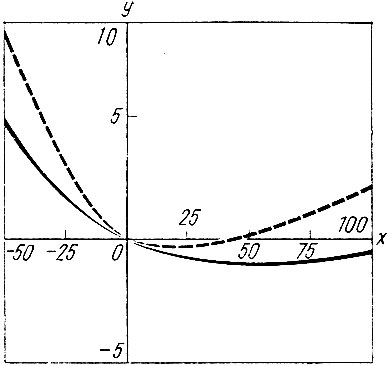
Рис. 34. Многопараметрический эксперимент (изменение в средней стоимости поездки в единицах времени): х - относительное изменение (в %) входных параметров по сравнению с их значением в НВБ; у - изменения (в %) в результате одновременного варьирования входными параметрами (сплошная линия), ожидаемое изменение в предположении его аддитивности по входным параметрам (пунктир)

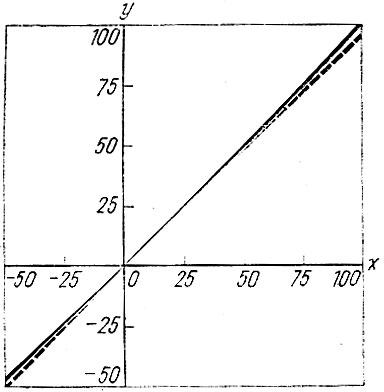
Рис. 35. Многопараметрический эксперимент - изменение в средней стоимости поездки (в денежных единицах): х - относительное изменение (в %) входных параметров по сравнению с их значением в НВБ; у - изменение в результате одновременного варьирования входными параметрами (сплошная линия), ожидаемое изменение в предположении его аддитивности по входным параметрам (пунктир)

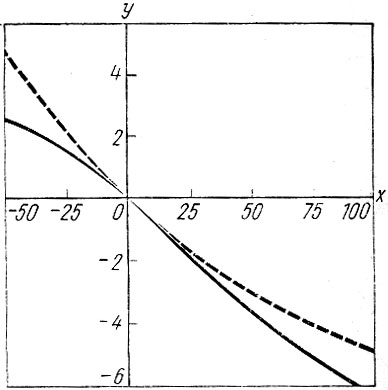
Рис. 36. Многопараметрический эксперимент: изменение в общем числе поездок из пригородов в центр г. Лидса: х - относительное изменение (в %) входных параметров по сравнению с их значением в НВБ; у - изменение (в %) в результате одновременного варьирования входными параметрами (сплошная линия), ожидаемое изменение в предположении его аддитивности по входным параметрам (пунктир)

В ходе эксперимента одновременно варьировались значения платы за проезд на общественном транспорте, время ожидания средств общественного транспорта, а также ценность времени (соответственно, эксперименты Н, I и М).

Рассматривая рис. 33, где приведены данные о числе поездок на индивидуальном транспорте, сразу видим, что последствия изменений параметров не аддитивны. Так, при раздельном удвоении платы за проезд на общественном транспорте, времени ожидания и ценности времени, число поездок на индивидуальном транспорте увеличивается соответственно на 9, 7 и 3,4% (суммарно 19,4%). В то же время одновременное варьирование этих параметров дает увеличение на 13%.

На рис. 34 и 35 отражены средние стоимости поездки соответственно во временных и денежных единицах. Разность их значений отражает учет в нашем эксперименте изменений в оценке ценности времени. Около начала координат кривые ведут себя почти идентично на всех четырех рисунках. Это соответствует нашему предположению о том, что выходные данные модели ведут себя как непрерывные функции и имеют непрерывные производные (приложение 2), а также показывает, что для малых изменений входных параметров результат изменения ряда выходных показателей можно с достаточной точностью определить как сумму отдельных изменений каждого из этих показателей. В то же время, при больших изменениях такая оценка ненадежна. В трех из четырех представленных на рисунках случаев кривые расходятся при больших значениях изменений в обе стороны от значений НВБ, причем величина расхождения приблизительно прямо пропорциональна квадрату величины изменения. Такое поведение можно было бы предвидеть исходя из общего соображения о том, что при рассмотрении какого-то выходного показателя модели в условиях изменения нескольких параметров ошибка в результате, полученном простым сложением результатов раздельного изменения каждого параметра, будет, как правило, оцениваться величиной смешанных производных. Иначе говоря, причиной расхождений будет прежде всего член, имеющий следующий вид:

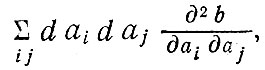
значение которого прямо пропорционально квадрату величины одновременного изменения параметров. При этом коэффициент пропорциональности равен

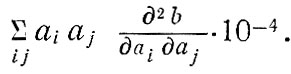
При более значительных изменениях все же возможно, что будет сказываться влияние производных более высоких порядков и две кривые могут сходиться или пересекаться. Действительно, представляется вполне вероятным, что это произойдет слева (в полуплоскости отрицательных значений) от области, изображенной на рис. 33, поскольку с приближением значения ценности времени к нулю владельцы легковых автомобилей захотят полностью перейти к пользованию самым дешевым (в денежном выражении) видом транспорта, т. е. общественным транспортом (для НВБ), и, следовательно, нужно ожидать сокращения на 100% числа поездок на индивидуальном транспорте, а также учесть дополнительное сокращение числа таких поездок вследствие снижения платы за проезд и величины времени ожидания до нуля, так что пунктирная линия на рис. 33 опустится ниже уровня - 100%, тогда как сплошная линия (поскольку она должна соответствовать некоторому положительному числу поездок на индивидуальном транспорте) не должна опускаться ниже уровня - 100%.

В рассмотренном нами частном случае (одновременное изменение платы за проезд, времени ожидания и ценности времени) главной причиной расхождения сплошной и пунктирной кривых является мультипликативная связь между платой за проезд и ценностью времени в оценке обобщенной стоимости. Так, показанное на рис. 34 влияние увеличения платы за проезд на среднюю стоимость поездки в единицах условного времени меньше, если одновременно увеличивается ценность времени, поскольку плата за проезд делится на величину ценности времени в выражении для определения обобщенной стоимости (см. раздел 2.3) и благодаря этому эффект снижения платы за проезд больше при низкой оценке времени. Таким образом, на рис. 34 сплошная линия расположена ниже пунктирной как для больших, так и для малых значений аргумента. Использование легковых автомобилей меняется с изменением разности между стоимостью поездки на общественном и индивидуальном транспорте, и на рисунке это изменение отражено сходным образом. Изменения (показанные как пунктирной, так и сплошной линиями) в средней стоимости поездки в денежном выражении, приведенные на рис. 35, определяются в основном влиянием изменения оценки времени, так что кажущееся хорошее совпадение может ввести в заблуждение. В этом случае причиной расхождения является совместное влияние ценности времени и времени ожидания. Точнее говоря, увеличение времени ожидания при оценке в денежных единицах имеет больший эффект при условии высокой ценности времени. Аналогично сокращение времени ожидания оказывает меньшее влияние при условии низкой оценки времени.

Мы не можем дать детального объяснения количественных изменений в числе поездок из пригородов в центр г. Лидса (см. рис. 36), поскольку на эту величину влияет как стоимость поездки на транспорте обоих видов, так и последствия конкуренции в начальных и конечных пунктах поездок, являющиеся результатом изменения стоимости поездок на других видах транспорта. Заметим, однако, что около начала координат можно наблюдать отклонение, размер которого прямо пропорционален квадрату величины изменения входных параметров.

В то же время для очень больших изменений может быть обнаружено влияние производных высших порядков.

Мы вправе сделать предварительный вывод о том, что для изменения значений входных параметров, не превышающих 25%, последствия изменений почти аддитивны в рассматриваемом случае и, вероятно, в большинстве прочих случаев, но аддитивная оценка становится все более ненадежной для более крупных изменений.

Очевидно, приемлемая степень ошибки должна зависеть от цели оценки.

По нашему мнению, для обеспечения следующего шага в итеративном процессе полученная нами оценка вполне удовлетворительна.