Приложения

Приложение 1. Обоснование конфигурации базовой модели

Было решено, что еще до проведения экспериментов по анализу чувствительности модели нужно оптимизировать тот ее состав, который будет использоваться в этих экспериментах. Учитывая ограниченность времени вычислений, главное внимание было уделено oсходимости в циклах наложения и распределения потоков. В принципе, модель, унаследованная от предшествующей работы, была аналогична изображенной на рис. 1 и отличалась лишь тем, что в ней наложение потоков осуществлялось четырьмя равными приращениями, а обращение к модели распределения потоков выполнялось лишь дважды.

Хотелось узнать, можно ли добиться сколько-нибудь существенного улучшения сходимости, приняв иные процедуры наложения и распределения пассажиропотока. В нашем распоряжении имелись программы, позволяющие получить потоки по многим маршрутам по Дайелу или Беррелу. Несмотря на то, что, как можно было ожидать, многомаршрутность ускорит сходимость процедур наложения пассажиропотоков, мы решили не пользоваться этими программами, потому что хотели по возможности сохранить ту форму модели, которой пользовались раньше для того, чтобы облегчить оценку и сравнение результатов наших экспериментов по анализу чувствительности с результатами предыдущей работы. В то же время использование процедур Дайела и Беррела было включено в число экспериментов по варьированию формы модели, и очевидно, что при заданном уровне затрат на вычислительные работы наши версии этих процедур дали менее удовлетворительную сходимость, чем процедура пошагового приращения пассажиропотоков.

Заметим, что в данное приложение не включены какие-либо результаты анализа итеративных процедур наложения пассажиропотоков.

Это отражает недостаточность наших ресурсов и тот факт, что у нас были основания полагать, что пошаговое приращение значений пассажиропотока обеспечивает лучшую сходимость, чем итеративные процедуры.

В наших первых экспериментах исследовалась связь между числом равновеликих приращений величины назначаемого пассажиропотока и сходимостью по первому критерию равновесия, предложенному Уолдропом [39]. Параметр сходимости А определяется формулой

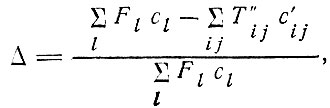
где F_l - поток по звену (l берется только для г. Лидса) в сети индивидуального транспорта; c_l - обобщенная стоимость проезда по звену l; Т_ij - число поездок из зоны i в зону j на индивидуальном транспорте; с_ij - минимальная обобщенная стоимость передвижения на индивидуальном транспорте из зоны i в зону j.

Сумма в знаменателе берется только по той части сети, для которой действует ограничение пропускной способности.

Рис. 37 показывает, в частности, отношение Δ к числу приращений пассажиропотока. Заметим, что скорость сходимости замедляется приблизительно после пяти приращений, так что, судя по наклону кривой, маловероятно, что данный метод назначения пассажиропотока может обеспечить подлинное равновесие без чрезвычайно большого и практически нереального числа приращений.

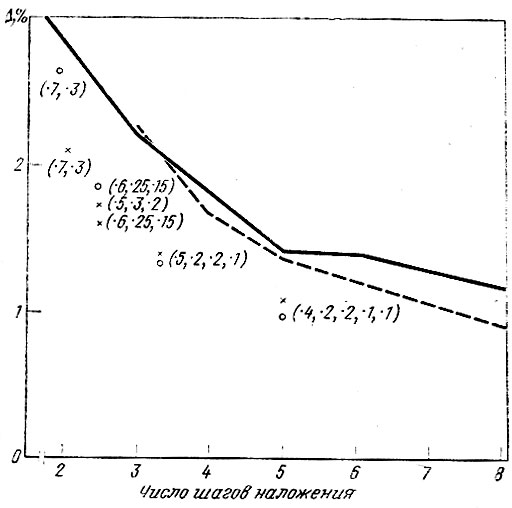
Рис. 37. Сходимость различных методов наложения потоков: Δ - величина расхождения (невязка) равна (∑_L f_L c_L - ∑_ij T_ij×c_ij)/×_L f_L c_L, где суммирование ведется по звеньям в районе г. Лидса. Сплошная - изменение невязки в незагруженной сети, пунктир - в перегруженной (величины шагов помечены кружком), крест - величины шагов приращения потока (в oскобках)

Интересно отметить, что была достигнута лучшая сходимость, когда начальная нагрузка накладывалась на загруженную сеть (данный тип назначения пассажиропотока обозначается CN в отличие от типа EN, в котором начальная нагрузка налагается на незагруженную сеть), кроме случаев, когда число приращений было мало.

Это, вероятно, определяется структурой сети, и в данном случае может, по-видимому, объясняться тем, что при немногочисленных приращениях первое из них и довольно большое ошибочно назначается на второстепенные пути (поскольку главные пути представляются уже перегруженными).

Не следует забывать, что значения Δ выведены из экспериментов и что на сделанные выводы сильно влияние принятой структуры сети (графство Западный Йоркшир по состоянию на 1974 г.), а также кривых изменения скорости и количества поездок, приходящихся на сеть индивидуального транспорта. Последнее соображение порождено тем, что большая плата за стоянку в г. Лидсе вызывала значительное перераспределение пассажиропотоков по видам транспорта в ущерб индивидуальным автомобилям, а также соответствующее крупное сокращение объема движения. В результате были получены значения Δ приблизительно в 0,8% для четырех равных по величине приращений.

При анализе чувствительности мы намеривались изменять значения числа итераций M и N на рис. 1) для того, чтобы добиться одинаковой сходимости для всех экспериментов. Однако:

хотя изменение в цикле М достигается очень просто, соответствующее изменение в цикле N в ходе вычислений требует сложной процедуры и может потребовать значительного машинного времени;

поскольку значения М и N дискретны, нельзя рассчитывать на получение одинаковой сходимости в разных экспериментах;

по техническим причинам предпочтительно иметь постоянные значения М и N.

Это приводит к заключению, что хотя и желательно изменять значения М и N, ограничения по времени и объему вычислительной работы вынуждают принять постоянные значения этих параметров. Выбирая какое-то значение для N, мы обратили внимание па результаты, приведенные на рис. 37 и 38, и приняли N=4 при неравных размерах приращений. Было значительно труднее определить соответствующее число необходимых циклов распределения потоков (значение М), но из рис. 39 следует, что, проведя три-четыре цикла, достигаем некоторой точки, после которой дальнейшие циклы мало влияют на объем поездок и величины затрат. Однако, если нас интересуют потоки, следует увеличить число циклов распределения до пяти-шести. Поскольку было намерение выполнять по нескольку расчетов на модели, мы обязаны были серьезно рассмотреть затраты машинного времени для каждого цикла, поэтому выбрали сочетание, состоящее из трех полных циклов (М=3), т. е. всего четыре распределения, каждое из которых состоит из четырех наложений потоков, взятых неравными долями из матрицы поездок в отношениях 5:2:2:1.

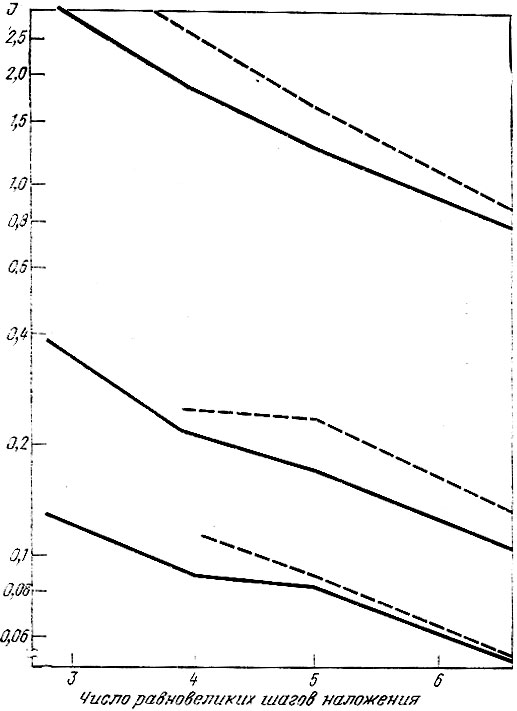
Рис. 38. Сходимость при равно великих шагах наложения потоков: I - параметр сходимости в логарифмическом масштабе, определяемый по формуле

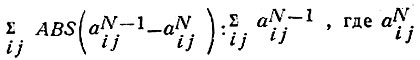
- элемент матрицы (потоков, поездок или стоимостей) после выполнения N шагов наложения. Верхняя пара кривых относится к потокам индивидуального транспорта, средняя - к поездкам на индивидуальном транспорте и нижняя - к стоимости поездок на индивидуальном транспорте. Пунктиром изображены кривые, относящиеся к наложению потоков в загруженной

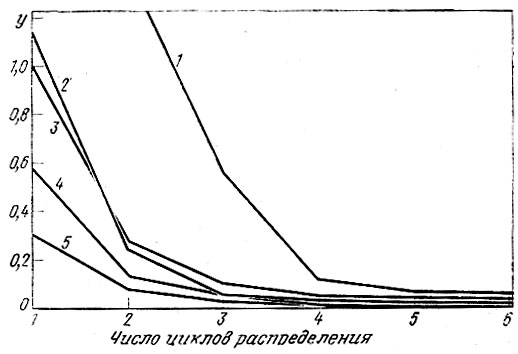
Рис. 39. Сходимость процедуры распределения; y - параметр сходимости, ∑_ij ABS×(a⁷_ij - a^M_ij)100/∑a⁷_ij, где a^M_ij является элементом матрицы потоков после М-то цикла. Ломаные на графике относятся к: 1 - потоку; 2 - поездкам Т²¹; 3 - поездкам T¹¹; 4 -стоимости поездок; 5 - поездкам T²²

В следующей серии проводившихся нами экспериментов предполагалось рассмотреть преимущества, получаемые при использовании неодинаковых по величине приращений. Результаты этих экспериментов также приведены на рис. 37. На базе этих данных делается вывод о том, что рациональное соотношение величин приращений позволяет весьма значительно улучшить показатель сходимости, приведенный в (1). Говоря конкретно, используя всего четыре приращения неодинаковой величины (в отношении 5:2:2:1), получаем сходимость, которая по приведенному показателю (п. 1.1.) равноценна сходимости с использованием семи равновеликих приращений.

В ходе экспериментов с различным числом пошаговых приращений был зарегистрирован индекс изменений, в матрицах поездок, стоимостей и пассажиропотоков, вызываемых последовательными приращениями. Для последнего N-го приращения числа поездок этот индекс равен

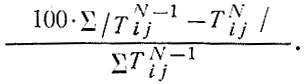
Выражения для изменений величин стоимости и размеров пассажиропотока аналогичны. На рис. 38 графически изображены результаты вычислений, выполненных для матриц индивидуального транспорта.

При сравнении результатов (N-1)-го приращения с результатами от N-го приращения видим, что объемы пассажиропотоков изменяются более заметно, чем число поездок, которое, в свою очередь, изменяется больше, чем значения стоимости. Мы занимаемся наложением потоков, и поэтому не удивляет, что они изменяются быстрее всего.

Тот факт, что число поездок изменяется быстрее значений стоимости, от которой оно зависит, определяется ограничивающими параметрами β. Следует ожидать, что величина относительного изменения Числа поездок будет в 100·β раз больше абсолютной величины изменения стоимости, что вполне согласуется с нашими предпосылками.

Сравнивая кривые, построенные для случая наложения потоков на загруженную сеть (ситуация CN), с кривыми, построенными для случаев наложения по пустой сети (ситуация BN), видим, что показатели для случая CN всегда изменяются больше, чем для EN. Сопоставив данный факт с получением меньших значений показателя сходимости в случаях перегрузки сети, приходим к выводу, что результаты вычислений в случае CN имеют больший разброс, чем в случае EN.

Возможной причиной этого является то, что при нашей матрице поездок и сети размер первого приращения в случае CN мог оказаться критическим и дестабилизирующим, поскольку пути, на которые ложится поток, могут оказаться второстепенными и к тому же с малой пропускной способностью.

На этом этапе мы сочли необходимым провести в одном расчете несколько циклов распределения потоков (цикл М на рис. 1), используя в каждом из них большое значение N для того, чтобы получить какой-то приближенный эталон для сравнения результатов других расчетов. Решили ограничиться семью полными циклами распределения пассажиропотока (М=7) с равными по величине приращениями величины потока (N=7). Лишь позже мы поняли, что могли добиться такой же точности при четырех неравных по величине приращениях, причем первое приращение каждого цикла накладывалось на загруженную сеть. Были проведены сравнения, аналогичные с показанными в формуле (2), а также (как один из вариантов использования этого выражения) сравнение каждой промежуточной матрицы поездок, стоимостей и потоков с полученными окончательными матрицами поездок, стоимостей и потоков. Результаты сравнения приведены на рис. 39 и позволяют сделать вывод о том, что после четырех полных циклов распределения заметного улучшения сходимости не происходит. Для каждого цикла наложения (согласно изложенному выше первому принципу Уолдропа) значения показателя сходимости показаны в табл. 1 (М означает число полных циклов распределения).

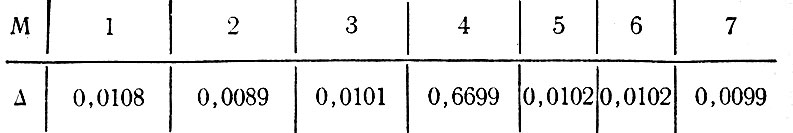
Таблица 1

Малый разброс приведенных значений Δ свидетельствует о том, что наш подход к исследованию сходимости цикла распределения не отражается сколько-нибудь заметно на сходимости процедуры наложения потока. Этого и следовало ожидать, поскольку любая связь между значением Δ и сходимостью цикла распределения достаточно слаба и существенна лишь при случайно изменяющихся структурах поездок.

Хотелось сравнить последствия изменения числа циклов распределения (М) с последствиями изменения числа циклов наложения потока (N). Это было важно потому, что для максимизации эффективности в смысле затрат машинного времени, нужна была соизмеримая точность наложения потока и его распределения по видам транспорта. В этом сравнении рассматривались значения формулы (9.2) для матриц поездок на индивидуальном транспорте. Обнаружилось, что изменение величины N с 5 на 6 (при M=2) дает значение 0,13, тогда как изменение величины М с 2 до 7 (при N=6) дает значение 0,35. Отсюда следует вывод о том, что при таких значениях М шести равных по величине приращений, по-видимому, более чем достаточно.

На этом этапе экспериментальной проверке были подвергнуты два новых метода ускорения сходимости. В принципе они заключались в том, что распределение вводилось в последовательность наложений потока таким образом, что полученное распределение непрерывно обновляется после каждого наложения потока и построения дерева кратчайших путей. В каждый момент пассажиропотоки складываются из некоторой доли предыдущих пассажиропотоков и какой-то части вновь назначенного числа поездок при постоянстве суммы пассажиропотоков для обоих видов транспорта. Эти два метода различались способом определения названных компонентов. Согласно первому из них, потоки сначала делились пополам, затем на четыре равные части, после чего производился "перебор", т. е. первая четверть пассажиропотоков заменялась новой четвертью и т. д. вплоть до получения какой-то сходимости. Согласно второму методу все прежние потоки постоянно сохранялись, но в постепенно уменьшающихся соотношениях на каждом этапе.

Полученные этими методами предварительные результаты оказались обнадеживающими в отношении значений Δ и выявления тенденции сходимости матриц поездок и стоимостей. Однако мы не располагали средствами для продолжения необходимых экспериментов. Интересующемуся данным вопросом читателю рекомендуется обратиться к работе С. Ивенса [22], где довольно глубоко и взаимосвязанно рассматриваются проблемы достижения сходимости для моделей наложения пассажиропотока и его распределения по видам транспорта, а также предлагается математическая программа рокфеллерского типа для получения одновременного решения.

После описанных в данном приложении экспериментов предстояло выбрать форму модели для анализа чувствительности. Несмотря на обнадеживающие результаты экспериментов с "перебором долей" и с "уменьшением долей", было решено отказаться от этих методов достижения сходимости, потому что они базируются на субъективных допущениях об адаптации к изменениям, отличающихся от тех, которые использовались на более ранних этапах нашей работы. Поскольку было желательно сравнить полученные результаты с данными этой более ранней работы, пришлось отказаться от этого направления исследования и остановиться на форме модели, сходной с уже использовавшейся ранее. Поэтому было решено сохранить форму, изображенную на рис. 1.