§ 2.3. Достоверность информации об аварийности

Эффективность использования информации об аварийности во многом зависит от того, насколько статистические данные точно отображают реальные процессы в структуре и динамике аварийности. В более узком смысле речь идет о достоверности тех показателей аварийности, которые получаются на основе данных, внесенных в карточку учета ДТП.

Опыт показывает, что в соответствии с методом определения и измерения достоверности большинство сведений, используемых при анализе аварийности, можно подразделить на три основные группы:

• количественные показатели, значения которых могут принимать непрерывный ряд значений;
• качественные характеристики с конечным числом различных значений (состояний);
• сводные статистические показатели о состоянии аварийности, полученные обобщением сведений о единичных ДТП.

Рассмотрим подробнее каждую из этих трех групп показателей, обратив особое внимание на определение достоверности, количественную меру для ее измерения и способы повышения достоверности сведений.

1. Достоверность количественных показателей, значения которых могут принимать непрерывный ряд значений. Прежде всего отметим, что требование о непрерывности возможных значений не означает их неограниченности. Как правило, такие показатели могут принимать различные значения, но в вполне ограниченном диапазоне. В качестве примеров показателей, относящихся к этой группе, можно привести длину тормозного пути, скорость транспортного средства, коэффициент сцепления с проезжей частью, глубину рисунка протектора и др. Очевидно, что значения этих показателей могут изменяться в весьма широком диапазоне, но этот диапазон в каждом конкретном случае имеет совершенно естественные ограничения.

Определение достоверности для показателей, принимающих непрерывный ряд значений, не представляет собой принципиальных трудностей - в подавляющем большинстве случаев она задается в виде ошибки измеряемого параметра. Ошибка может задаваться либо в тех же единицах, что и измеряемый параметр (скорость транспортного средства в момент происшествия равнялась 50 ± 2 ^км/_ч, длина тормозного пути 9,5 ± 0,3 м и т. д.), либо в процентах относительно среднего значения.

Способ вычисления ошибки в значительной мере зависит от источника этой ошибки. Применительно к задачам анализа сведений о ДТП можно выделить два основных источника ошибки в значениях измеряемого параметра.

Прежде всего это так называемая инструментальная погрешность, связанная с точностью измерительного инструмента. Например, если глубина рисунка протектора измеряется с помощью щупа, имеющего миллиметровое деление, то ошибка измеренного параметра не может быть меньше 1 мм. В данном случае очевидны не только способ вычисления ошибки, но и пути повышения достоверности данных - для получения более точных значений необходим более точный инструмент.

Второй источник ошибки в значениях измеряемого параметра состоит в том, что различные измерения одного и того же параметра дают различные значения, даже если они производятся одним и тем же инструментом. Например, измерив глубину рисунка протектора на разных участках шины колеса, мы можем получить десятки различных значений измеряемого параметра, имеющих весьма значительный разброс. Еще больший разброс значений можно получить, если необходимо обобщить сведения не по одному происшествию, а по группе различных происшествий.

Наиболее часто применяемый подход к оценке ошибки по результатам многих измерений заключается в расчете доверительного интервала (ошибки) при заданной доверительной вероятности {9, 26].

Пусть по данным измерений х₁, х₂,...,х_n рассчитана средняя величина: 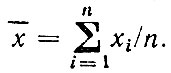Очевидно, что 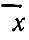не обязательно совпадает с истинным значением оцениваемого параметра х и в общем случае существует отличная от нуля разность величин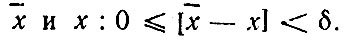

Положительное значение δ задает ошибку и характеризует в соответствии с нашим определением достоверность измеряемого параметра. Ясно, что чем меньше значение δ, тем больше достоверность результатов измерений. Однако статистические методы не позволяют категорически утверждать, что неравенство 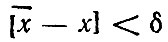будет выполняться во всех случаях, каким бы большим не было значение δ. Как правило, справедливость этого неравенства утверждается только с некоторой вероятностью у, которая называется "доверительной вероятностью". Обычно доверительную вероятность задают равной 0,95; 0,99 или 0,999 и при известном ее значении вычисляют ошибку δ. Интервал 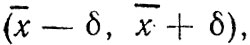который покрывает неизвестное значение параметра х с вероятностью γ, называется "доверительным

интервалом".

Между доверительной вероятностью и доверительным интервалом существует однозначная связь: чем большую доверительную вероятность мы задаем (т. е. с чем большей надежностью мы хотим определить результат), тем больше будет допустимый интервал ошибок и, наоборот, мы можем уменьшить ошибку, но при этом возрастут шансы того, что в каждом конкретном случае фактическое значение параметра будет выходить за пределы интервала ошибки.

Для нормального распределения х₁, х₂,...,х_n ошибка параметра δ вычисляется по формуле [12]

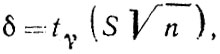
(2.1)

где n - число измерений значения х; 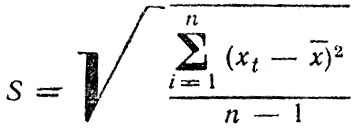- выборочная дисперсия; t - коэффициенты Стьюдента.

Значение коэффициентов Стьюдента t_γ вычисляется достаточно сложными специальными методами. Для практического использования их обычно находят по таблицам, которые приводятся в большинстве учебных и справочных изданий по математической статистике. В табл. 2.2 приведены значения t_γ для некоторых значений γ и n.

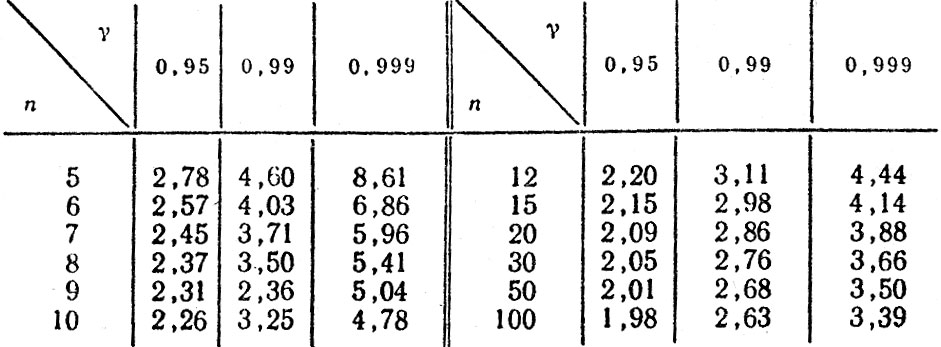
Таблица 2.2. Значения коэффициентов Стьюдента

Рассмотрим конкретный пример оценки достоверности измеряемого параметра.

При испытаниях тормозной системы автомобиля проводилось 7 торможений, начиная со скорости 60 ^км/_ч до полной остановки. В результате получены следующие значения длины тормозного пути: 10,6 м; 11,2; 11,8; 10,9; 12,0; 10,2; 11,4 м. Среднее значение тормозного пути 11,2 м. Необходимо оценить достоверность (ошибку) данного параметра.

По табл. 2.2 для n = 7 и γ = 0,95 находим t_γ = 2,45. Вычисляем выборочную дисперсию

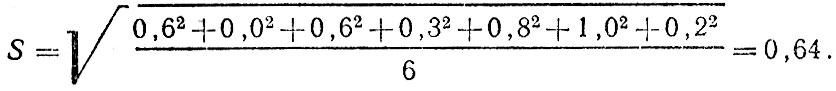
Подставляя эти значения в формулу для расчета δ, окончательно получаем: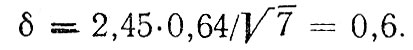

Таким образом, длина тормозного пути находится в интервале 11,2 ± 0,6 м. Ошибка измерений составляет ±6,4%.

Сократить доверительный интервал можно, либо увеличивая число измерений n, либо уменьшая доверительную вероятность.

2. Достоверность качественных характеристик с конечным числом различных значений (состояний). Типичной характеристикой такого рода является "вид ДТП", который подразделяется на столкновения, опрокидывания, наезды на пешеходов и т. д.. Искажение информации о виде происшествия может произойти либо в результате ошибки при заполнении карточки учета ДТП; либо в результате неправильного установления вида происшествия. В любом случае достоверность сведений количественно характеризуется вероятностью того, что информация в любой произвольно взятой карточке будет правильной.

Оценить достоверность таких показателей можно только фактической проверкой по первичным документам, оформленным на месте ДТП. Допустим, что при проверке 50 случайным образом выбранных карточек учета ДТП ошибки в заполнении реквизита вид ДТП обнаружены в двух карточках, т. е. достоверность сведений о виде ДТП p = 48:50 = 0,96.

Полученная оценка достоверности не означает, однако, что каждый раз, когда мы произвольным образом выберем, например, 100 карточек, то именно в 96 карточках будет правильно заполнен реквизит "вид ДТП". В каждом конкретном случае их число может оказаться больше или меньше 96. Как и в случае с параметрами, значения которых могут принимать непрерывный ряд значений, выход заключается в задании доверительной вероятности γ и вычислении доверительного интервала δ. Значение δ в этом случае вычисляется по формуле (2.1), но выборочная дисперсия вычисляется по другой формуле [9]:

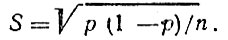
В нашем примере n = 50; р = 0,96. Задав доверительную вероятность γ = 0,99, находим значения S и δ:

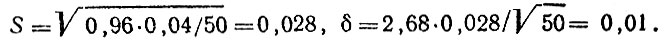
Таким образом, достоверность сведений о виде ДТП будет равна 0,96 ± 0,01, т. е. с вероятностью 0,99 не более 5 % карточек учета ДТП будут иметь ошибки при заполнении реквизита.

Аналогичным образом может быть оценена достоверность по каждому возможному значению характеристики ДТП. В частности, в предыдущем примере мы рассматривали 50 произвольных карточек учета ДТП и любое искажение информации о виде ДТП считали ошибкой. Можно поступить по-другому: отобрать, например, 50 случаев наездов на пешехода, а затем проверить, правильно ли указан вид ДТП в карточках учета. Тем самым мы получим достоверность сведений об одном конкретном виде происшествий - наезде на пешеходов.

При использовании вероятности правильного заполнения сведений в качестве оценки достоверности следует особое внимание уделять случайности отбираемых карточек. Например, если все отобранные карточки были заполнены одним лицом, то существует реальная возможность внесения систематической погрешности за счет того, что это лицо неправильно трактует правила учета ДТП или по другой причине.

Если обеспечивается случайность выбора, то число карточек, по которым следует проводить проверки, относительно невелико. Из приведенной выше формулы видно, что максимальное выборочное значение 5 получается при р = (1 - р) = 0,5. В этом случае 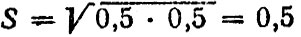и значение доверительного интервала 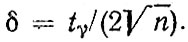Из этого соотношения можно получить выражение для приблизительной оценки числа карточек, подлежащих проверке, n = ^t_γ2/₄ δ².

Например, если мы хотим обеспечить точность оценки достоверности данных с разбросом не более чем δ = 0,01, то при t_γ = 2,68 получаем n = 67. Таким образом, для получения оценки достоверности данных с требуемой точностью^ нужна проверка не более чем 67 карточек учета ДТП.

3. Достоверность статистических показателей о состоянии аварийности, полученных обобщением сведений о единичных ДТП. Оценка достоверности обобщенных показателей о состоянии аварийности представляет собой наибольший практический интерес.

Как правило, под достоверностью сводных данных понимается полнота учета ДТП. Количественная оценка полноты учета сводится к проведению сверок данных о ДТП с медицинскими учреждениями, учреждениями Госстраха, а также с автотранспортными предприятиями и организациями. Правилами учета ДТП предусматривается, что такие сверки должны проводиться не реже 1 раза в месяц.

Рассмотрим конкретный пример. В целом по городу за месяц включены в государственную статистическую отчетность сведения о 46 ДТП с пострадавшими. В результате проведения сверки выявлено еще 9 происшествий, сведения о которых подлежат включению в отчетность. Следовательно, фактически в городе за месяц произошло 55 происшествий, из которых только 46 включено в отчетность и достоверность сводных данных о количестве ДТП с пострадавшими р = 46/50 = 0,84. Задав доверительную вероятность γ = 0,99, получим следующее значение

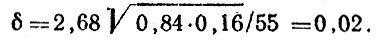
Таким образом, с большой долей уверенности мы можем утверждать, что только 82-86 % происшествий в городе включаются в государственную статистическую отчетность и именно эти цифры следует считать оценкой достоверности данных о ДТП.

Путь обеспечения достоверности сводных данных о состоянии аварийности один - безусловное выполнение требований Правил учета и прежде всего своевременное проведение сверок с медицинскими учреждениями, учреждениями Госстраха и с автотранспортными предприятиями.