§ 4.2. Понятие вероятности. Построение гистограмм и распределений

Мы уже неоднократно сталкивались с объективно существующим разбросом данных измерения одного и того же показателя относительно некоторого среднего значения. Например, в § 2.3 приводился пример измерения глубины рисунка протектора шины. Какими бы точными методами мы не пользовались, измерения в разных местах дадут разные результаты. Увеличивая число измерений мы только все более точно будем оценивать реально существующий разброс значений, но устранить его таким способом, естественно, невозможно.

Такая ситуация характерна для большинства данных, используемых при анализе аварийности, и следует отчетливо понимать, что при объективно существующей степени неопределенности при любых выводах будет существовать некоторая вероятность ошибки. Поэтому изучение математических методов необходимо начать с понятия вероятности.

Так называемое статистическое определение вероятности заключается в том, что за вероятность некоторого события принимается относительная частота появления этого события в достаточно большом числе испытаний. Например, если при проверке 1 тыс. автомобилей у 150 оказались неправильно отрегулированными световые приборы, то вероятность наличия такой неисправности для любого случайным образом выбранного автомобиля можно принять равной 150/1000 = 0,15. Точное значение этой вероятности можно установить, только проверив все автомобили, число которых в данном случае называется генеральной совокупностью. Мы же вычисляем искомую вероятность только по 1 тыс. автомобилей, т. е. сделав некоторую выборку из генеральной совокупности. Поэтому полученное значение вероятности называют выборочной вероятностью или оценкой вероятности. В дальнейшем в этой главе ко всем параметрам, которые рассчитываются не на основе генеральной совокупности, а на основе выборки, мы будем добавлять слово выборочная: выборочное среднее, выборочная дисперсия и т. д.

Большинство показателей, характеризующих ДТП, может принимать множество различных значений: возраст пострадавшего - от 1 года до 99 лет, скорость транспортного средства от 0 до 100-150 ^км/_ч и т. д. Естественно, что какие-то из этих значений встречаются чаще, а какие-то реже. Эту частоту мы описывали удельными показателями и говорили, что их набор характеризует структуру аварийности. Удельные показатели могут служить достаточно наглядным описанием структуры аварийности, но пользоваться ими для сравнения различных структур все же не всегда удобно, особенно если число различных значений переменной велико.

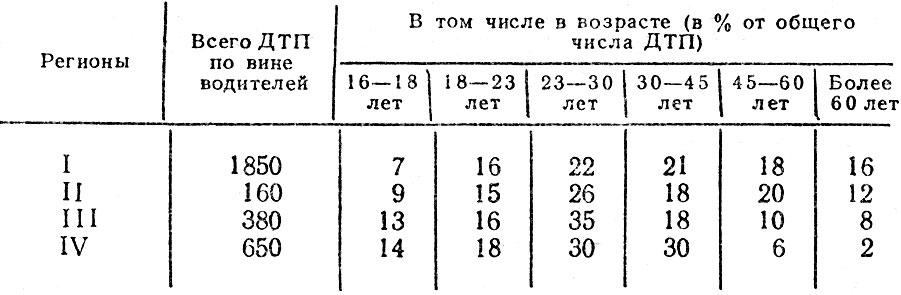
Таблица 4.1. Распределение по возрасту водителей, виновных в совершении ДТП, %

Например, в табл. 4.1 приведены доли ДТП, совершенных по вине водителей различного возраста от общего числа ДТП для четырех разных регионов. Сопоставляя приведенные удельные показатели, можно говорить, что структура аварийности приблизительно одинакова в I и II, а также в III и IV регионах, но существенно различается в I и III, а также во II и IV регионах. Однако эти различия мы не можем выразить количественно и установить четкую границу между схожими и различными структурами аварийности.

Методы математической статистики позволяют проводить такое сравнение, используя специальные характеристики случайных величин: выборочное среднее и выборочную дисперсию.

Выборочное среднее вычисляется по хорошо известному соотношению

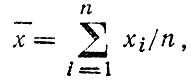
где n - число измерений значения х; x_i - значения на разных ДТП.

В табл. 4.2 приведен средний возраст водителей, виновных в совершении ДТП, для тех же регионов, что и в в табл. 4.1

Таблица 4.2. Средние значения и выборочные стандартные отклонения для возраста водителей, виновных в совершении ДТП

Сравнение средних подтверждает ранее сделанный вывод о том, что регионы I и II, III и IV попарно более схожи между собой, чем I и IV. Однако следует иметь в виду, что в некоторых случаях средние значения могут не только не принести пользу, но и ввести в заблуждение. Связано это с тем, что когда говорится о среднем значении, интуитивно предполагается, что это среднее значение встречается чаще других, причем вероятности проявления 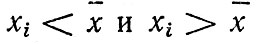симметричны относительно среднего. На практике это может оказаться далеко не так. Например, из табл. 4.1 видно, что в регионе II по вине водителей старше 45 лет совершено 32 % всех происшествий, а в регионе IV - только 8 % и наоборот: водителями в возрасте от 23 до 45 лет в регионе IV совершено 60 % происшествий, а в регионе II - 44 % Можно утверждать, что в регионе II наблюдается более равномерное распределение водителей по возрасту, чем в регионе IV, или, что то же самое, возраст водителей в регионе IV имеет меньшее рассеяние, разброс относительно среднего, нежели в регионе II. Меру рассеяния наиболее часто оценивают величиной

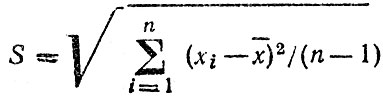
Значение S называют выборочным стандартным отклонением, а S² - выборочной дисперсией. В табл. 4.2 представлены вычисленные стандартные отклонения возраста виновных водителей относительно среднего значения для тех же четырех регионов. Как видим, разброс значений в регионе IV значительно меньше не только по сравнению с регионами I и II, но и по сравнению с регионом III.

Выборочная средняя и выборочная дисперсия дают достаточно полную, но не исчерпывающую характеристику случайной величины. Все необходимые сведения о случайных переменных содержат так называемые плотности вероятности или статистические распределения вероятностей [9].

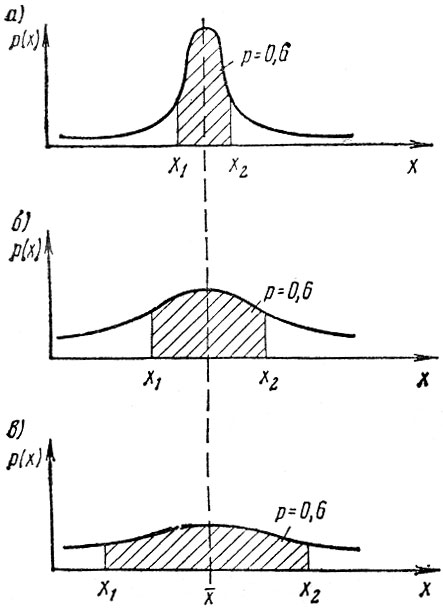
Рис. 4.1 Симметричные статистические распределения с одинаковым средним и различным рассеиванием: а - маленьким; б - нормальным; в - большим

На рис. 4.1 представлены 3 вида статистических распределений случайной величины х, имеющих одинаковое среднее значение, но различную дисперсию, рассеивание относительно среднего. На этих графиках по горизонтальной оси отложены возможные значения х, а по вертикальной - плотность вероятности появления каждого конкретного значения х.

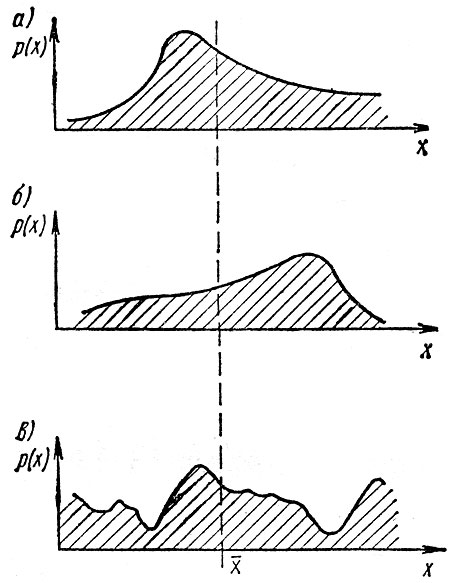
Рис. 4.2. Несимметричные статистические распределения с одинаковым средним: а - чаще фиксируются значения х меньше среднего; б - чаще фиксируются значения х больше среднего; в - сложная форма статистического распределения

На рис. 4.2 и 4.3 изображены более сложные случаи, когда распределение вероятности появления различных значений х несимметрично относительно среднего, хотя средние значения одинаковы. Из вида распределений со всей очевидностью следует, что они соответствуют совершенно различным и несопоставимым по своей природе процессам. Следовательно, два параметра - среднее и дисперсия не всегда могут полностью охарактеризовать случайную величину.

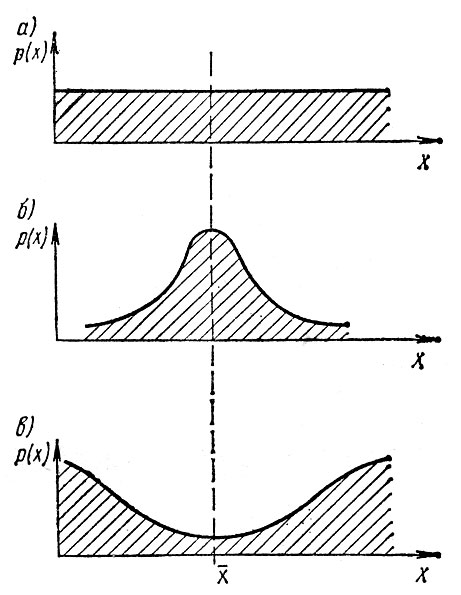
Рис. 4.3. Симметричные статистические распределения с одинаковым средним: а - вероятности фиксации всех возможных значений х одинаковы; б - среднее значение х фиксируется наиболее часто; в - среднее значение х фиксируется реже других значений

Зная вид распределения, можно вычислить вероятность попадания х в любой заданный интервал значений. Она будет равна площади под кривой распределения. На рис. 4.1 площадь, задающая вероятность того, что х₁≤х≤х₂ заштрихована и равна 0,6. Следует обратить внимание на то, что для распределений с большей дисперсией интервал возможных значений при одной и той же вероятности попадания в него расширяется. Поскольку х в результате измерения обязательно примет какое-нибудь значение, то общая площадь под кривой статистического распределения всегда должна равняться 1.

Когда на практике часто встречается один и тот же вид распределения, целесообразно описать его с помощью математической формулы. Число широко применяемых на практике распределений невелико. Мы рассмотрим четыре из наиболее часто встречающихся распределений: нормальное, Стьюдента, пуассоновское и биномиальное. С другими видами распределений можно ознакомиться в специальных изданиях [23]

Нормальное распределение имеет симметричную куполообразную форму, аналогичную изображенной на рис. 4.1, и описывается следующей формулой

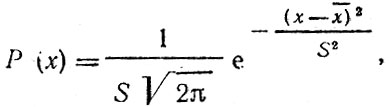
где 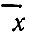- среднее значение случайной величины х; S - стандартное отклонение.

Нормальное распределение имеют случайные величины и события, на возникновение которых влияют многочисленные - не зависящие друг от друга факторы, которые не могут быть точно зафиксированы и учтены при проведении анализа. Такая ситуация является типичной для многих процессов и явлений в природе, технике, в социальных системах. Это обусловливает широкое распространение нормального закона распределения в статистических исследованиях.

Имеются и другие особые свойства нормального распределения, которые обусловливают его частое использование В частности, нормальное распределение имеет сумма достаточно большого числа различных случайных величин, даже если каждая исходная переменная распределена не по нормальному закону. Многие специальные распределения при определенных условиях с достаточно хорошей точностью заменяются нормальным распределением и т. д.

Вероятность попадания нормально распределенной случайной величины х в интервал (х₁, х₂) рассчитывается с использованием функции Лапласа Φ (z) [9, 12]:

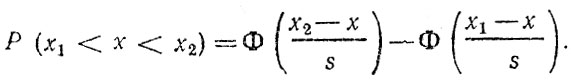
Функция Лапласа обычно приводится в виде таблиц в специальных изданиях по математической статистике. В табл. 4.3 приводится часть этой таблицы для некоторых значений z. При пользовании таблицей следует иметь в виду, что Φ(-z) = - Φ (z).

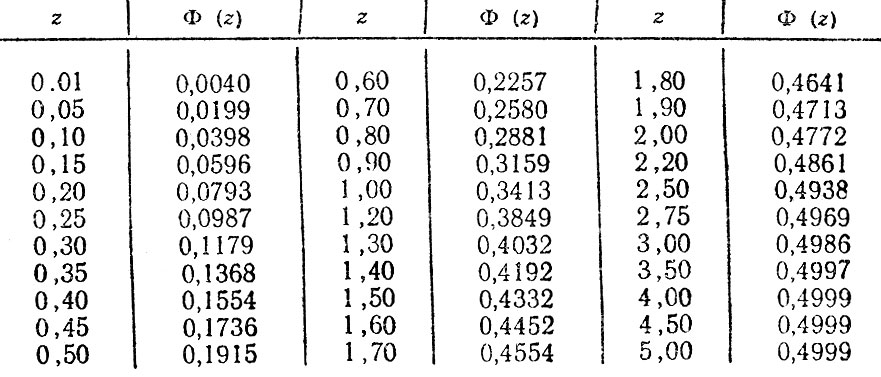
Таблица 4.3. Значения функции Лапласа

Пример. При исследовании попутных столкновений в городах измерялась дистанция между транспортными средствами до начала торможения Получено, что дистанция распределена по нормальному закону со средним значением 30 м и стандартным отклонением 10 м. Найти вероятность того, что дистанция между транспортными средствами находится в интервале 10-50 м. Воспользуясь функцией Лапласа и сведениями из табл. 4.3, получим

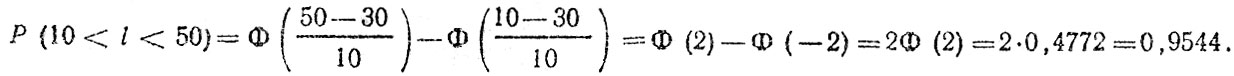
Эти результаты можно трактовать следующим образом: 95 % всех наездов на впереди идущее транспортное средство совершается при дистанции 10-50 м до начала торможения, и только в 5 % случаев дистанция бывает большей 50 или меньшей 10 м.

Распределение Стьюдента (t-распределение). В нормальном законе распределения мы в качестве параметров использовали среднее значение 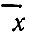и стандартное отклонение S. Однако следует иметь в виду, что эти параметры рассчитаны по выборке ограниченного объема со случайными значениями х и, следовательно, 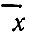и S сами являются случайными величинами. Если число исходных измерений невелико, то это может существенно исказить результаты анализа.

Английский статистик У. Госсет, публиковавший свои работы под псевдонимом У. Стьюдент, в 1908 г. нашел решение этой проблемы. Он доказал, что отклонение выборочного среднего значения от фактического среднего можно оценить на основе специальной переменной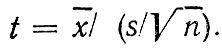

Аналитическое выражение распределения случайной величины достаточно сложно, и мы его рассматривать не будем, поскольку, как и функция Лапласа, она приводится в специальных изданиях в табличном виде. Использование t-распределения Стьюдента не имеет принципиальных отличий от нормального распределения. Отметим только, что распределение Стьюдента обычно используют не для расчета вероятности попадания случайной величины в заданном интервале, а, наоборот, по заданной вероятности определяется интервал возможных значений. Особенностью распределения Стьюдента является и то, что его значения зависят от числа степеней свободы, которое на единицу меньше числа исходных данных n. С ростом n распределение Стьюдента быстро приближается к нормальному, и уже при n>30 оно с большой точностью заменяется нормальным.

Биномиальное распределение. До сих пор мы рассматривали распределения показателей, которые могут иметь непрерывный ряд значений. Между тем при анализе аварийности многие показатели являются дискретными и могут принимать только вполне определенные значения. Например, число ДТП, число погибших и раненых могут принимать только целые значения, водитель может совершить только вполне определенное, но не дробное число нарушений Правил дорожного движения и т. д.

Пусть некоторое событие А наступает с вероятностью р. Тогда вероятность того, что в n случаях событие А наступит k раз рассчитывают по формуле:

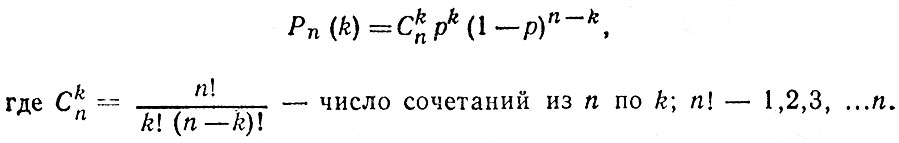
Данное распределение называют биномиальным и его использование рассмотрим на конкретном примере.

Пример. В целом по автотранспортному управлению на 1 тыс. единиц транспортных средств приходится 12 ДТП в год, т. е. вероятность участия одного транспортного средства ДТП равна р = 0,012. Какова вероятность того, что в автотранспортном предприятии, имеющем 100 автомобилей, будет совершено не более 3 происшествий в год, если работа по ОБДД там проводится на среднем для управления уровне (т. е. для транспортных средств этого автотранспортного предприятия р = 0,012)? Используя биномиальное распределение, получаем:

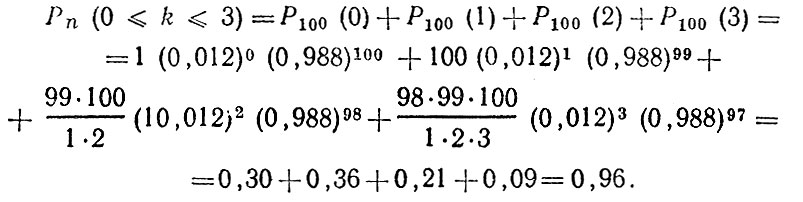
Таким образом, с вероятностью 0,96 в автотранспортном предприятии может быть совершено до трех ДТП в год

Распределение Пуассона. Расчеты по формуле биномиального распределения становятся излишне громоздкими при больших n и малых p. В этих случаях используют распределение Пуассона

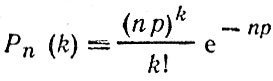
Как и биномиальное, распределение Пуассона является дискретным и позволяет вычислять вероятность k появлений события А в n испытаниях, если вероятность появления события А в одном испытании равна р. Пуассоновское распределение достаточно точно заменяет биномиальное уже при р<0,1. В свою очередь, пуассоновское распределение переходит в нормальное и с большой точностью заменяется им при np>9, т. е. в этом случае дискретное распределение заменяется непрерывным, что еще более упрощает проведение расчетов.

Зная вид функции распределения, как мы уже убедились, можно достаточно просто вычислить необходимые вероятностные характеристики случайной величины. Однако перед этим следует убедиться, что распределение случайной величины соответствует тому, которое мы собираемся использовать.

Таблица 4.4. Проверка гипотезы о виде распределения скоростей движения транспортных средств при наездах на пешеходов

Установление вида распределения начинают с визуальной оценки формы распределения по гистограмме. Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой являются интервалы изменения значения х, а высоты равны частоте попадания этого значения в каждый интервал. В табл. 4.4 в первой колонке представлены интервалы скоростей движения транспортных средств до начала торможения при наездах на пешеходов, а во второй - частота ДТП для каждого интервала, полученная по 366 случаям. На рис. 4.4 изображена гистограмма этого распределения.

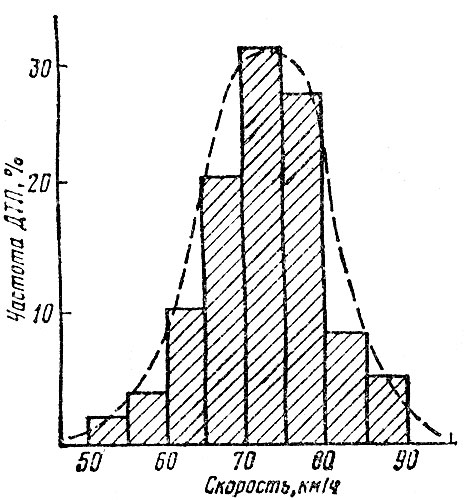
Рис. 4.4. Гистограмма, распределения скоростей транспортных средств яри наездах на пешеходов

По виду гистограммы можно предположить, что распределение имеет нормальный закон. Однако необходимо по возможности точно убедиться, что это так. Имеется много разных критериев проверки соответствия фактического и теоретического распределений [23, 26].

Наиболее часто используют критерий Пирсона. Заключается он в следующем.

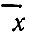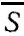1. Рассчитывают и по всей совокупности исходных данных и находят теоретические частоты ДТП в предположении о нормальности распределения скоростей. В табл. 4.4 теоретические частоты представлены в колонке 3.

2. Обычно теоретические и фактические частоты различаются, поэтому в качестве меры различий вычисляют

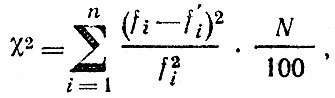
где f_i - фактические частоты; f'_i - теоретические частоты; N - общее число измерений.

В четвертой колонке табл. 4.4 приводится расчет для рассматриваемого примера.

3. Задают уровень значимости - допустимую вероятность ошибки нашего вывода. В большинстве случаев уровень значимости полагают равным 0,05, т. е. допускается 5 %-ная возможность ошибки в заключении о нормальности распределения частот.

4. Делают заключение о нормальности закона распределения. Доказано,, что случайная величина х² имеет специальное распределение с k = z - r - 1 степенями свободы, где: z - число групп (интервалов) в выборке (в нашем примере скорости перед началом торможения разбиты на 8 интервалов, следовательно, z = 8); r - число параметров в проверяемом распределении (для нормального закона r = 2: среднее значение и стандартное отклонение). Обычно использование χ² распределения сводится к определению по таблицам допустимого отклонения χ²_max при заданном уровне значимости и известном числе степеней свободы. В табл. 4.5 приведены значения χ²_max для уровня значимости 0,05.

Для k = z - r - 1 = 8 - 2 - 1 = 5 степеней свободы находим χ²_max = 11,1.

Поскольку фактически в нашем примере χ² равно 7, 19, т. е. χ²<χ²_max, то у нас нет оснований отвергать гипотезу о нормальности анализируемого распределения. Если бы фактическое значение χ² было больше 11,1, то при уровне значимости 0,05 мы должны были бы отвергнуть гипотезу о том, что скорости в нашем примере имеют нормальное распределение.

Аналогичным образом критерий χ² можно использовать и для проверки гипотез о других видах распределений. Изменяться при этом будет только метод вычисления теоретических частот.