§ 4.3. Проверка значимости в статистических исследованиях

Мы уже говорили о сопоставлении как основном приеме статистического анализа. В процессе анализа приходиться сравнивать, сопоставлять различные показатели - сводные данные о состоянии аварийности, усредненные значения возраста, стажа, удельные и относительные показатели и т. д. В большинстве случаев эти показатели рассчитываются на основе исходных данных с ограниченным объемом. Поэтому выводы и заключения, которые делаются в результате сопоставления, как отмечалось, имеют некоторую степень неопределенности. Чтобы избежать при этом грубых ошибок, приходится проводить специальное исследование, которое в математической статистике называется проверкой значимости.

Наиболее часто встречающиеся случаи, когда в процессе сопоставления приходится проводить проверку значимости, рассмотрим на конкретных примерах.

1. В одном регионе средний возраст водителей, совершивших ДТП, равен 31,4 годам, а в другом - 34,2 года. Можно ли считать эту разницу существенной и сделать вывод о том, что во втором регионе ДТП совершаются водителями более старшего возраста?

Решение этой задачи называется проверкой значимости различий между выборочными средними и заключается в проверке некоторой гипотезы [12]. Например, мы выдвигаем гипотезу о том, что средний возраст водителей, виновных в совершении ДТП, в обоих регионах одинаковый и существующее различие объясняется случайностью выборки.

Выдвинутая гипотеза может быть правильной или неправильной. Поскольку проверка производится статистическими методами, в итоге проверки могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через α и называть уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если принято α = 0,05, то это значит, что в пяти случаях из 100 мы рискуем допустить ошибку первого рода, т. е. отвергнуть правильную гипотезу.

Процедура проверки справедливости выдвинутой гипотезы о равенстве средних значений состоит в следующем:

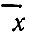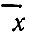• по критериям, приведенным в предыдущем параграфе, проверяем, что переменные X₁ и X₂ имеют нормальное распределение. Вычисляем средние значения ₁ и ₂, а также дисперсии S²₁ и S²₂;
• фиксируем уровень значимости, например α = 0,01 или α = 0,05;
• вычисляем
  
  
  где n₁, n₂ - объемы выборки для первой и второй переменной соответственно.

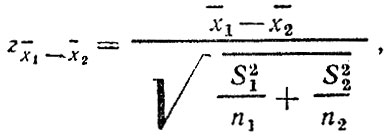
Переменная z - нормально распределенная случайная величина со средним значением 0 (мы проверяем гипотезу о равенстве средних) и дисперсией I. Вероятность ее отклонения на величину, большую чем z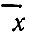_1-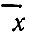2, рассчитывается по обычной функции Лапласа:

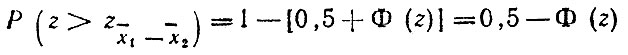
Следовательно, если [0,5 - Φ(z)]<α, то мы должны отвергнуть гипотезу и признать разницу между х₁ и х₂ значимой. Если же [0,5 - Φ(z)]>α, то у нас нет оснований отвергнуть гипотезу о равенстве средних.

Пример. Изучены сведения о 100 ДТП с участием велосипедистов и 50 ДТП с участием водителей мопедов. В первом случае средний возраст оказался равным 17,16 года и стандартное отклонение - 0,67 года. Во втором - средний возраст 17,49 года и стандартное отклонение 0,64 года. Значение переменной z

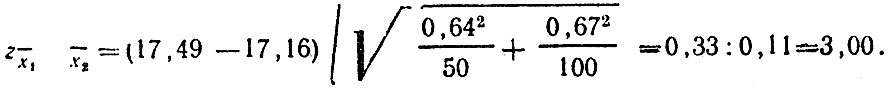
По таблицам получаем: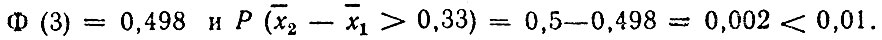

Таким образом, на уровне значимости по крайней мере 0,01 мы должны отвергнуть гипотезу о равенстве возраста велосипедистов и водителей мопедов и признать имеющуюся разницу значимой.

Следует высказать несколько замечаний относительно использования критериев значимости на практике.

Во-первых, значение z и предложенный способ проверки значимости применимы для достаточно больших выборок: n₁ и n₂ должны быть по крайней мере больше 3,0. Если же объемы выборок малы, то следует использовать не нормальное z-распределение, t-распределение Стьюдента. Во-вторых, если выдвинутая гипотеза не отвергается, то это еще не значит, что она доказана. Правильнее говорить - данные наблюдений согласуются с гипотезой о равенстве средних и не дают оснований ее отвергнуть. Этот факт необходимо иметь в виду при интерпретации результатов проверки значимости.

В-третьих, если даже гипотеза отвергается, нельзя категорически утверждать о значимости различий, поскольку каким бы малым не был уровень значимости а, он не равен нулю. Рано или поздно при повторном проведении проверок могут появиться значимые различия. Поэтому единичный результат со значимой разницей не может служить исчерпывающим доказательством. Следует проводить повторные выборки, давать содержательное объяснение полученным результатам.

В-четвертых, проверяемая гипотеза может заключаться не только в предположении о равенстве средних. Можно сформулировать и проверить, например, гипотезу о том, что 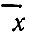₁ больше 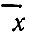₂ на величину а. Тогда числитель в формуле для расчета z будет равен 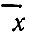₁ - (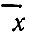₂ + а).

Могут быть сформулированы и другие более сложные гипотезы.

2. Второй часто встречающийся на практике случай, когда приходится проводить проверку значимости - сопоставление частот (оценок вероятности) одних и тех же событий.

Пусть по выборкам из n₁ = 360 и n₂ = 580 ДТП по вине водителей получено, что в первом случае 18,6 % водителей находилось в нетрезвом состоянии, а во втором 19,4 % (т. е. вероятность того, что в случайно выбранном дорожно-транспортном происшествии водитель находится в нетрезвом состоянии в первом случае равна р₁ = 0,186, а во втором р₂ = 0,194). Следует ли считать существующее различие значимым?

Проверка значимости в этом случае не имеет принципиальных отличий от предыдущего случая, когда проверялось различие средних:

• формулируем гипотезу о равенстве вероятностей;
• фиксируем уровень значимости α = 0,005, или α = 0,01;
• вычисляем
  
  
  если 0,5 - Φ (z_p2-p1)<α, то гипотезу о равенстве р₂ и р₁ отвергаем. В противном случае имеющиеся данные не позволяют отвергнуть выдвинутую гипотезу. В нашем примере: ;
  
  

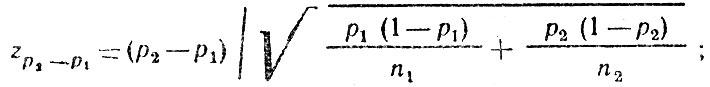
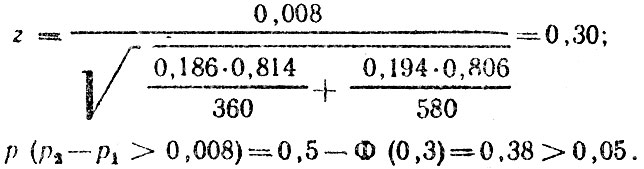
Следовательно, гипотеза о равенстве доли дорожно-транспортных происшествий по вине нетрезвых водителей в двух регионах не отвергается.

3. Третий случай проверки значимости мы рассмотрим применительно к изменению (динамике) показателей аварийности.

Для того чтобы оценить значимость изменения показателей аварийности во времени, важно таким образом выбрать случайную величину, чтобы она допускала простое проведение расчетов.

В качестве такой величины удобно использовать вероятность попадания транспортного средства (ТС) в ДТП. Выбор этот обусловлен тем, что распределение оценки вероятности р = ^m/_n, (где m - число ДТП, n - число ТС) можно с большой точностью аппроксимировать нормальным распределением со средним np и дисперсией S² = р (1 - р)/_n.

Следовательно, для сопоставления вероятностей мы можем использовать метод проверки значимости, изложенный выше. Рассмотрим изменения показателей аварийности во времени при двух различных гипотезах.

Гипотеза 1. 3а два аналогичных периода времени в одном регионе получены две оценки вероятности попадания ТС в ДТП: р₁ = ^m₁/_n1 и р₂ = ^m₂/_n2;

Выдвигается гипотеза, что разница р₂ - р₁ объясняется ограниченностью объема выборки и фактически р не изменялась, т. е. р = const. На основании имеющихся данных

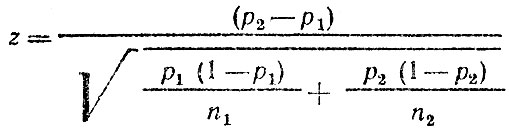
и далее проводится проверка значимости по уже известной процедуре. На практике часто решают обратную задачу:

при известном уровне значимости а из соотношения 0,5 - Φ (z_Д) = α находят максимально допустимое значение z_Д (например, для α = 0,05 z_Д = 1,96), а затем из уравнения:

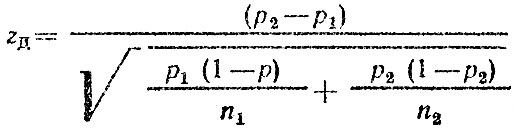
находят допустимое отношение числа ДТП за два аналогичных периода, которое можно признать незначимым,

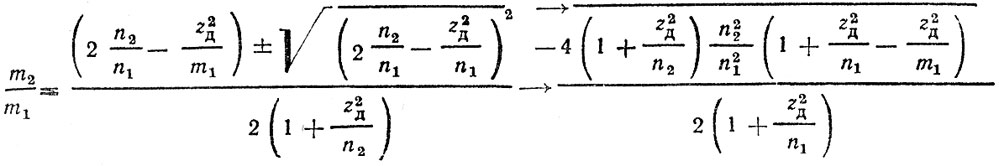
Если умножить это выражение на 100, то оно позволяет вычислить верхнее и нижнее возможные изменения показателей аварийности в процентах к аналогичному предшествующему периоду времени.

Недостаток этой формулы заключается в самой гипотезе - предположении о постоянстве р. В условиях постоянного роста парка ТС эта гипотеза предполагает, что абсолютное число ДТП (m₁ и m₂) должно расти, т. е. фактически мы проверяем гипотезу о том, что число ДТП растет теми же темпами, что и парк ТС. Поэтому целесообразно рассмотреть еще одну гипотезу.

Гипотеза 2. Постоянным остается абсолютное число ДТП, т. е. m₂ = m₁.

Если эта гипотеза верна, то должны выполняться равенства: р₁ = ^m₁/_n1 и р₂ = ^m₂/_n2.

Если же фактически m₂ ≠ m₁, то за второй отрезок времени р₂ будет другим: р'₂ = ^m₂/_n2 ≠ ^m₁/_n2 = p₂.

Следовательно

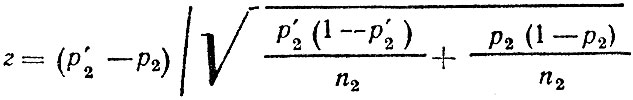
Определив по уровню значимости α допустимое значение z, можно рассчитать и допустимое изменение абсолютных показателей аварийности:

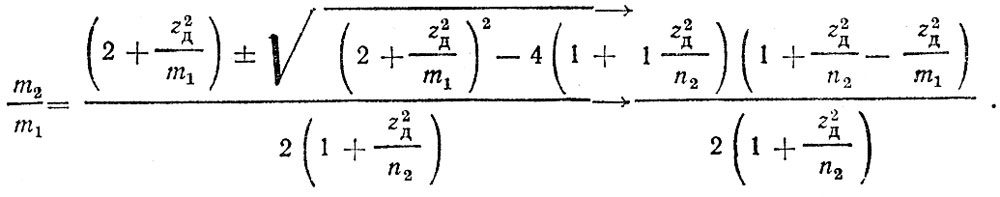
Полученные выражения достаточно просто вычисляются с помощью микрокалькуляторов. В табл. 4.6 представлены расчетные данные о допустимых изменениях показателей аварийности для некоторых m₁ и n₂ при уровне значимости α = 0,005.

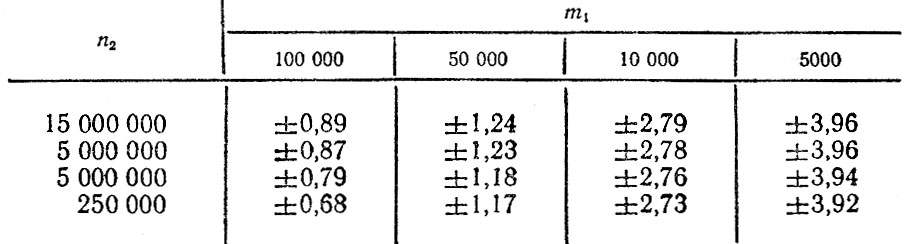
Таблица 4.6. Допустимые изменения показателей аварийности при α = 0,05 (в %)

Необходимо особо оговорить особенности применения полученных расчетных соотношений. "Допустимые" изменения здесь никак не связаны с оценкой деятельности и не означают, что любые изменения в "допустимых" пределах следует считать приемлемыми. Речь идет о том, что в рамках имеющихся данных разброс показателей аварийности в этих пределах статистически не объясняется, является незначимым. Поэтому как бы подробно мы не анализировали статистические данные, окончательные выводы, сделанные без привлечения дополнительных сведений, могут оказаться недостаточно достоверными.

Полученные выражения дают возможность с помощью относительно простых вычислений разделить все изменения показателей аварийности на значимые и незначимые. Такое разделение позволяет исключить бессмысленное сопоставление малоразличающихся показателей и производить при необходимости целенаправленный поиск дополнительной информации для объяснения причин относительно небольших изменений показателей аварийности.