§ 4.4. Оценка взаимозависимости показателей

Во многих задачах анализа аварийности требуется установить и оценить степень зависимости различных показателей между собой. Все существо анализа данных в основном состоит в установлении взаимосвязей между различными переменными. При этом, конечно, не всегда речь идет об установлении взаимосвязи в виде некоторого математического соотношения. Очень часто анализ проводится без построения формальных моделей, но в каждом случае, пусть даже неосознанно или интуитивно, для получения окончательных выводов приходится делать заключения относительно характера взаимозависимости анализируемых показателей.

Количественная оценка степени взаимозависимости показателей требует прежде всего четкого и точного определения понятия взаимозависимости. В настоящее время не выработана и по существу отсутствует единая, общепринятая классификация и терминология в этой области. Однако при рассмотрении анализа аварийности как этапа подготовки и выработки управляющего решения определяющим признаком характера связи между различными показателями является степень их взаимозависимости. Мы рассмотрим три различные степени взаимозависимости между различными показателями, которые наиболее часто встречаются в практике анализа аварийности.

Отсутствие зависимости. На первый взгляд, доказательство такого утверждения выглядит тривиальным. Однако на практике это может оказаться даже более сложной задачей, чем подтверждение причинной связи. Отсутствие какой связи доказывается? Не связано ли это с действием побочных факторов, не учитываемых в данном анализе? Насколько мала должна быть степень зависимости, чтобы признать ее отсутствующей? Эти и целый ряд других вопросов не только сильно усложняют, но и могут сделать неразрешимой задачу установления отсутствия связи.

Ценным является и само заключение об отсутствии зависимости между теми или иными показателями. Во многих ситуациях такой вывод дает не меньше оснований для выбора и обоснования мероприятий по предупреждению ДТП, чем установление причинной связи и количественная оценка степени влияния того или иного фактора на состояние аварийности.

Простая взаимосвязь. Связанными называются переменные, которые изменяются одновременно в одном и том же или в противоположных направлениях. Так, существует очевидная связь между временем суток и тяжестью последствий ДТП, стажем и возрастом водителей и т. д. Взаимосвязь между показателями может существенно искажать или изменять выводы и результаты анализа.

Методы установления взаимосвязи показателей хорошо разработаны в математической статистике. Ниже будет рассмотрен один из наиболее широко применяемых из них - корреляционный анализ. Наиболее широко используемыми показателями количественной оценки степени связи переменных являются коэффициенты корреляции и регрессии.

Отметим, что установление простой связи между двумя или несколькими признаками далеко не всегда достаточно для принятия управленческих решений. Как правило, выбор и обоснование мероприятий по ОБДД требуют установления причинной связи между зависимыми показателями.

Причинная зависимость. Мы уже отмечали, что мероприятия по предупреждению ДТП должны планироваться таким образом, чтобы устранить или ослабить причины, порождающие аварийность. Поэтому установление причинных связей является совершенно необходимым этапом выработки управленческого решения. Наличие простой связи между переменными не дает никаких оснований для вывода о существовании причинной зависимости. Если не проводить дальнейших исследований, такие выводы могут привести к значительным и неоправданным затратам. Пример такого вывода приводит Р. Акофф [2]. Этот пример не связан с деятельностью по предупреждению ДТП, однако он весьма нагляден и мы его полностью процитируем.

В одном из крупных американских городов проводилось исследование зависимости заболевания туберкулезом от загрязнения воздуха сажей. Для этого территорию города разбили на районы с равной площадью и в каждом из них определили количество сажи, выделяемой в атмосферу в течение года, и заболеваемость туберкулезом. Обнаружив сильную положительную зависимость, исследователи пришли к выводу о том, что сажа вызывает туберкулез. В связи с этим были проведены дорогостоящие мероприятия по сокращению выбросов дыма в атмосферу. Воздух стал чище, однако заболеваемость туберкулезом не уменьшилась.

Дополнительное, более тщательное исследование показало,- что причина высокой положительной связи между загрязнением воздуха и заболеваемостью туберкулезом заключается в другом. Оказалось, что чем сильнее воздух загрязнен сажей, тем меньше желающих жить в таком районе и тем меньше квартирная плата. Чем ниже квартирная плата, тем больше семей с низким доходом живет в таком районе и тем больше здесь вероятность заболевания туберкулезом, так как в таких семьях хуже уровень медицинского обслуживания, они больше страдают от плохого питания и т. д. Эти причины и порождали более высокую заболеваемость туберкулезом.

Ошибочные рассуждения иногда могут способствовать избавлению от чего-то плохого (в приведенном выше примере - от загрязнения воздуха), но это не может служить подтверждением правильности выводов, поскольку поставленная цель при этом не достигается.

Установление причинной связи, обусловленности значений одних показателей другими, а не наоборот, представляет собой весьма сложную задачу и при анализе аварийности. Например, общеизвестно, что ДТП в ночное время имеют повышенную тяжесть последствий и езда ночью более опасна. Допустим, что мы анализируем ДТП, совершаемые водителями-мужчинами и водителями-женщинами, и обнаружили, что мужчины более часто управляют автомобилем в ночное время. Следует ли из этого, что женщины реже ездят ночью из-за опасности, либо езда ночью более опасна из-за того, что ночью автомобилями преимущественно управляют мужчины? Ответ на этот вопрос невозможно получить, имея только сведения об аварийности и интенсивности движения. Необходимы привлечение дополнительных сведений, проведение испытаний, более подробное изучение причин и т. д.

Можно утверждать, что причинная зависимость является наиболее важным видом взаимозависимостей различных факторов. Наша способность анализировать и делать правильные выводы существенно зависит от того, насколько хорошо мы представляем себе причинные связи. Многие неудачи борьбы с аварийностью, по-видимому, объясняются тем, что мы либо допускаем существование причинной связи там, где она отсутствует, либо неправильно характеризуем причинную связь, которая действительно существует

Задача установления причинной зависимости усложняется тем, что в системе ОБДД связь между показателями аварийности и факторами, влияющими на их значения, редко бывает простой и очевидной. Сложные проблемы редко имеют простые решения, т. е. решения, связанные только с одной переменной, с одной причиной. На состояние аварийности влияет множество факторов, и действие одного из них может заменяться и искажаться другими. Такую зависимость нелегко понять и трудно обнаружить. Но даже незначительное, частичное улучшение понимания происходящих явлений способно привести, хотя и длинным путем, к эффективному решению очень сложных проблем.

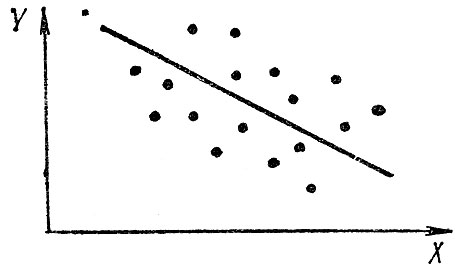
Рис. 4.5. Совокупность наблюдений с небольшой дисперсией

Один из таких методов, позволяющих улучшить понимание происходящих процессов,- расчет и изучение корреляционных связей между показателями. Под корреляционной зависимостью обычно понимается наличие линейной связи между двумя переменными, когда рост или снижение одного показателя сопровождается пропорциональным изменением другого. На рис. 4.5 представлена совокупность из 18 пар наблюдений двух показателей Y и X. Можно легко заметить, что существует определенная тенденция, в соответствии с которой большим значениям X соответствует меньшее значение Y и наоборот. Коэффициент корреляции дает количественную характеристику этой тенденции, т. е.

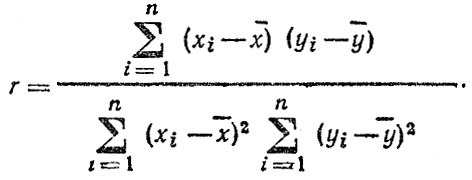
Значение коэффициента корреляции может изменяться от +1 до -1. Крайние значения соответствуют функциональной линейной связи между X и F, когда все точки наблюдений находятся строго на одной прямой. Расчет и изучение коэффициентов корреляции позволяют получить дополнительные сведения для анализа причин роста или снижения аварийности, изменений в ее структуре. Например, в табл. 4.7 даны коэффициенты корреляции числа ДТП с тремя из факторов, влияющих на аварийность.

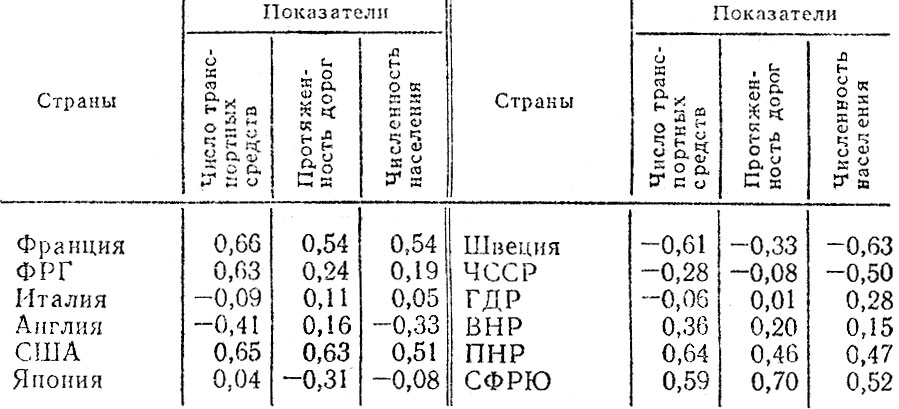
Таблица 4.7. Коэффициенты корреляции числа ДТП с показателями, влияющими на состояние аварийности

Из табл. 4.7 видно, что существует определенная связь между числом ДТП и объективно действующими на состояние аварийности факторами, причем связь числа ДТП с численностью парка транспортных средств выше, чем с протяженностью дорог и численностью населения. Если рассматривать эти факторы как возможные причины роста аварийности, то можно отметить, что большее значение коэффициента корреляции говорит о недостаточной управляемости происходящих процессов. В то же время в таких странах, как ГДР, ЧССР, Япония, Италия, удалось преодолеть влияние этих факторов и состояние аварийности мало зависит от их действия.

Коэффициент корреляции может быть рассчитан для всевозможных пар исходных показателей. Например, если число исходных показателей равно 20, то может быть рассчитано 190 различных коэффициентов. Поэтому для удобства пользования принято располагать коэффициенты корреляции в виде матриц,, В табл. 4.8 приведена матрица корреляции между некоторыми показателями, используемыми в анализе аварийности. Коэффициенты корреляции между любой парой показателей находятся на пересечении соответствующей строки и колонки. Название показателей приведены только в строках, а в колонках для краткости указаны только их соответствующие номера. Матрица симметрична относительно своей диагонали (коэффициенты корреляции X с Y я Y с X равны), поэтому приводится только нижняя часть матрицы. Все коэффициенты корреляции рассчитаны по большой выборке по данным за 30 лет.

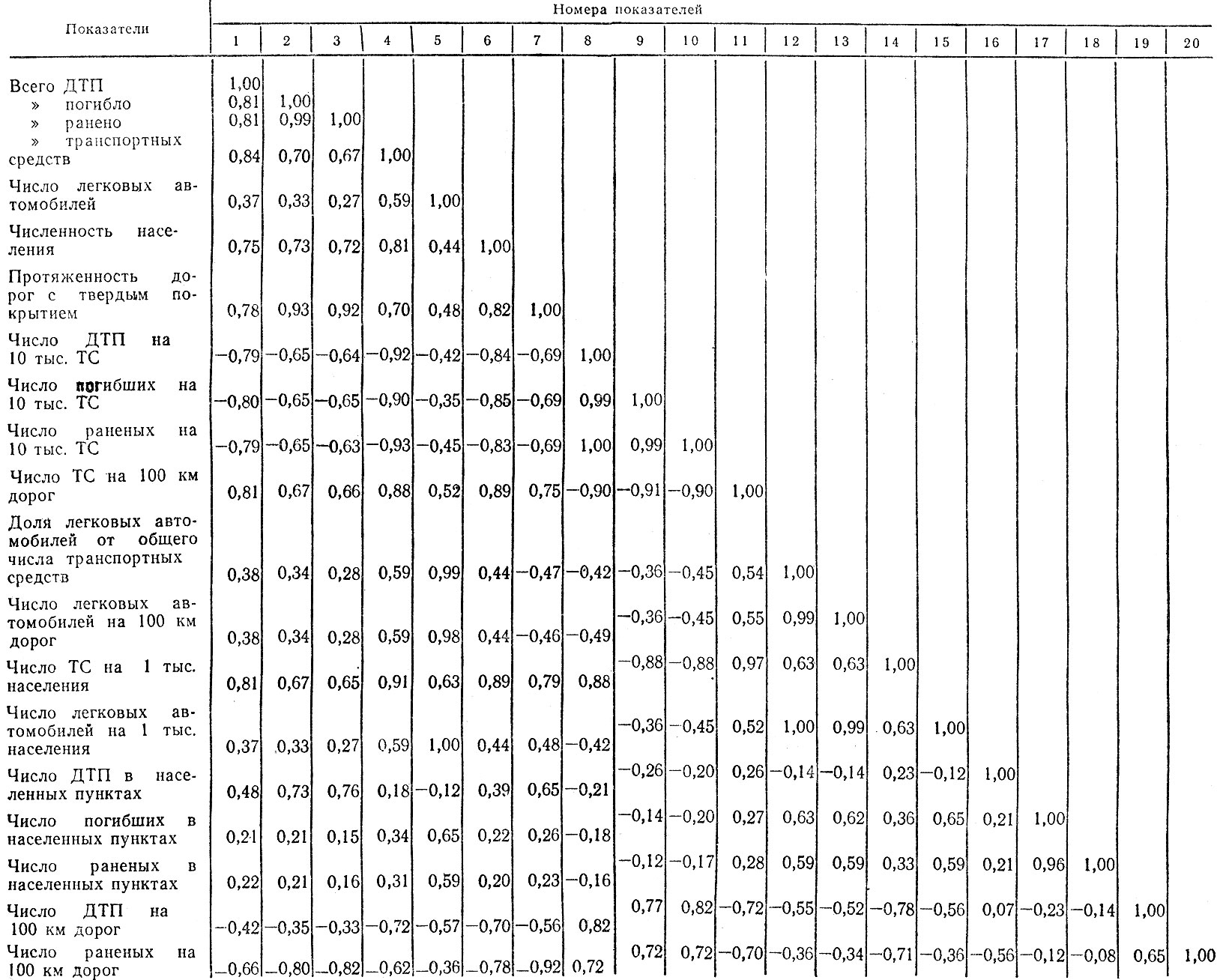
Таблица 4.8. Матрица коэффициентов корреляции

Наличие высокого коэффициента корреляции, как мы уже отмечали, говорит только о наличии связи между показателями, но не причинной зависимости. Поэтому факт большого значения коэффициента корреляции может быть использован только для того, чтобы определить, какие из многочисленных переменных следует отобрать для дальнейшего исследования с целью выявить существование причинных зависимостей. В то же время маленькое значение коэффициента корреляции еще не говорит об отсутствии причинных зависимостей.

Во-первых, коэффициент корреляции зависит не только от наклона, но и от разброса фактических данных относительно прямой линии, На рис. 4.6 угол наклона прямой, которая отражает тенденцию изменений X и Y тот же, что и на рис. 4.5, но разброс точек относительно этой линии выше. Поэтому и коэффициент корреляции в этом случае меньше. Между тем такой разброс может объясняться, например, воздействием большего числа неучитываемых в анализе факторов, а не ослаблением причинной зависимости.

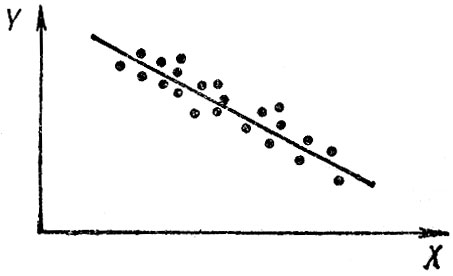
Рис. 4.6. Совокупность наблюдений с большой дисперсией

Во-вторых, коэффициент корреляции отражает только наличие линейной связи. На рис. 4.7 изображены данные о двух совокупностях наблюдений, В обоих случаях просматривается четкая связь переменных X и F, но коэффициент корреляции будет близок к 0, поскольку взаимозависимость носит нелинейный характер. Такого рода зависимости не могут анализироваться" с помощью коэффициентов корреляции, а требуют более сложных методов.

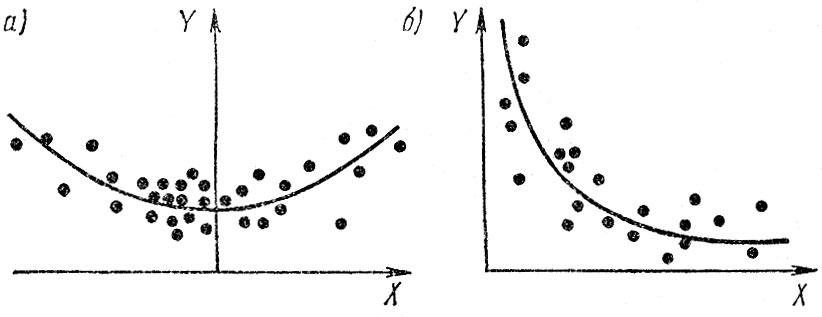
Рис. 4.7. Примеры нелинейной связи переменных: а - параболическая; б - гиперболическая

Большая степень взаимосвязи между показателями позволяет избежать еще одной широко распространенной ошибки при анализе показателей аварийности. Ниже приводятся распределения числа ДТП в зависимости от двух тесно связанных факторов - возраста и стажа водителей:

Как следует из представленных данных, наибольшая доля дорожно-транспортных происшествий приходится на водителей в возрасте от 27 лет до 41 года и со стажем от 2 до 3 лет. Напрашивается вывод о том, что именно с этой группой водителей необходимо активизировать профилактическую работу. Еще раз отметим, что такой вывод не исключает необходимости установления причины повышенного уровня аварийности в этой возрастной группе. В частности, причина может заключаться в том, что группа водителей в возрасте от 27 до 41 года наиболее многочисленна. Поэтому следует подсчитать относительный показатель - число ДТП к числу водителей в каждой возрастной группе - и продолжить анализ и т. д. Однако нам известно, что возраст и стаж тесно связаны между собой и одновременно влияют на состояние аварийности. Следовательно, и анализировать их следует в комплексе.

В табл. 4.9 представлены сведения о распределении числа ДТП одновременно по возрасту и стажу. Таблица составлена по тем же данным, которые использовались по подготовке ранее приведенных распределений числа ДТП по возрасту и стажу водителей отдельно.

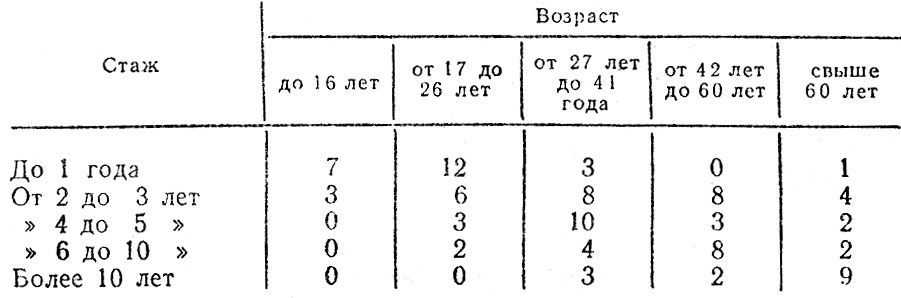
Таблица 4.9. Распределение числа ДТП по возрасту и стажу водителей, виновных в совершении ДТП, %

Из сведений, приведенных в табл. 4.9, следует, что если в соответствии с ранее сделанными выводахми планировать и проводить мероприятия с водителями в возрасте от 27 лет до 41 года и со стажем от 2 до 3 лет, то мы будет воздействовать на группу водителей, совершивших всего 8 % ДТП. Между тем, если выбрать группу водителей в возрасте от 17 до 26 лет и со стажем работы до 1 года, то мы смогли бы воздействовать на водителей, совершивших 12 % ДТП. Следовательно, анализ в предыдущих примерах был проведен неточно и разработанные на его основе мероприятия были бы недостаточно эффективными.

Ошибка возникла из-за того, что первоначально мы использовали одномерные распределения, а затем - двумерные. Для связанных между собой показателей выводы одномерного и многомерного анализов могут иметь существенно-различающийся результат. Если учесть, что многие показатели, характеризующие условия и причины возникновения ДТП, связаны между собой, а большинство мероприятий по предупреждению ДТП разрабатывается и обосновывается на основе методов одно-двумерных распределений, то можно предположить, что недостаточная эффективность профилактической работы объясняется и неправильным выбором "узких мест" в деятельности по ОВДД. Выход из положения заключается в использовании многомерных методов анализа, однако их практическое использование сталкивается с двумя основными трудностями.

Во-первых, чрезвычайно большое число взаимосвязанных факторов, подлежащих анализу, делает невозможной их ручную обработку. Без применения ЭВМ удается анализировать только двумерные распределения (таблицы) и с большим трудом трехмерные (наборы таблиц). Анализ четырех и более факторов может проводиться только на ЭВМ. Это требует применения специальных методов и программ обработки многомерных данных.

Во-вторых, по мере увеличения числа анализируемых факторов происходит деление общего числа ДТП на все более мелкие группы с более индивидуальными признаками. В результате мы выделим "узкое место", которое будет содержать незначительную по численности группу ДТП.

Разрешить противоречие между необходимостью многомерного анализа и "дроблением" общего числа ДТП можно, переформулировав задачу выявления "узкого места" следующим образом. Сначала задается объект воздействия - некоторая доля ДТП от общего их числа (20 %, 40 % и т. д.). Затем, используя многомерные методы, определяют значения анализируемых факторов так,чтобы на них приходилось не менее заданного числа дорожно-транспортных происшествий, а разброс значений факторов был минимален. Допустим, что на основе сведений в табл. 4.9 нам необходимо выбрать интервалы возраста и стажа водителей так, чтобы, проводя профилактическую работу среди этих водителей, мы воздействовали не менее чем на 40 % ДТП. Эти

40 % можно составить из различных комбинаций цифр, имеющихся в таблице, но наименьший разброс значений факторов (две градации по возрасту и три по стажу) получается, если мы выберем водителей в возрасте от 17 лет до 41 года и со стажем до 5 лет, которыми совершается 42 % ДТП.

Точное решение подобного рода задач может быть осуществлено только методами полного перебора. Однако применить его удается только при сравнительно небольшом числе анализируемых факторов. Если же число анализируемых факторов превышает 10-15, а число ДТП - несколько сотен, то реализовать метод полного перебора не удается даже с помощью самых мощных ЭВМ.

Для приближенного решения подобного рода задач разработан специальный метод, основанный на построении теоретического многомерного распределения (аналогично тому, как определяли параметры нормального распределения на основе гистограммы в § 4.2). Этот метод реализован на ЭВМ и позволяет достаточно точно восстанавливать истинные распределения достаточно общего вида, в том числе при взаимосвязи признаков и наличия среди них показателей, не имеющих количественного измерения.

Другой подход к решению этой задачи состоит в применении не полного, а направленного перебора различных сочетаний значений признаков, характеризующих условия и причины возникновения ДТП. Первоначально отбирают наиболее часто встречающееся сочетание признаков. Затем к нему добавляют другие группы ДТП, которые не только встречаются чаще других, но и имеют наименьшие отличия значений признаков по сравнению с ранее отобранными. Процесс продолжается до тех пор, пока число отобранных ДТП не достигнет величины, на которую предполагается воздействовать.

Эта процедура носит в значительной мере эмпирический характер, но она не требует сложных расчетов и позволяет достаточно просто обрабатывать большие массивы информации. В частности, обработка реальных данных о ДТП по трем характеристикам (день недели, время суток и место совершения) показала, что уже 40 % дорожно-транспортных происшествий включают в себя все дни недели, 21 из 24 ч суток и 80 % мест дорожно-транспортных происшествий. Между тем одномерный анализ каждой из трех характеристик в отдельности дает принципиально другой результат, наличие ярко выраженных пиков в конце недели, а также в утренние и вечерние часы. Если мы собираемся проводить мероприятия, связанные со всеми тремя характеристиками одновременно (например, решать задачу расстановки сил и средств дорожно-патрульной службы), то необходимо планировать их исходя из многомерного анализа. В противном случае мероприятия могут оказаться недостаточно эффективными.