§ 4.5. Модели прогнозирования

В предыдущем параграфе мы отмечали, что правильное установление причинно-следственных связей между различными показателями и факторами является одним из основных условий результативности анализа данных о ДТП. Следующий шаг, естественное желание любого исследователя - количественно оценить возможные последствия предполагаемых воздействий или бездействия, т. е. составить прогноз состояния аварийности для тех или иных конкретных условий.

Бурное развитие прогностики как науки в последние десятилетия привело к созданию множества методов, процедур, приемов прогнозирования. По оценкам зарубежных и отечественных ученых, уже насчитывается свыше 150 методов прогнозирования, различных по своим функциям и далеко не равноценных по своему значению [16]. Из их числа можно выделить три основных подхода к разработке прогнозов.

1. Анкетирование (интервьюирование, опрос) экспертов. В отличие от прогнозов, составляемых отдельными лицами на основе их субъективных представлений о возможном изменении состояния аварийности в будущем, экспертный опрос позволяет упорядочить, увеличить степень объективности прогнозов. Хотя анкетирование с целью подготовки прогнозов и имеет свои особенности, однако эти особенности не вносят принципиальных изменений в порядок проведения и в общие методы обработки результатов экспертного опроса, изложенные в § 8.5. Поэтому здесь на прогнозировании методами экспертного опроса мы останавливаться не будем.
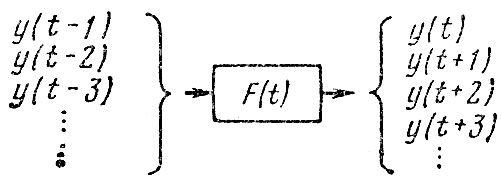
2. Поисковый прогноз на основе оценки динамики изменения показателей аварийности и прогнозирование состояния аварийности в будущем при условии, что сложившиеся тенденции сохранятся. Построение модели для прогнозирования показателя аварийности заключается в нахождении зависимости
   y = F (t),
   где y - прогнозируемый показатель аварийности; t - время; F (t) - неизвестная функция. Вид функции определяется ка основе данных о значении показателя y в предшествующие периоды времени:
   
   
   Такой прогноз называется поисковым потому, что он отвечает на вопрос: что вероятнее всего произойдет при условии сохранения существующих тенденций? При этом следует иметь в виду, что, полагая неизменными сложившиеся тенденции развития аварийности, мы не учитываем возможные решения и действия, способные радикально изменить тенденции. Если в соответствии с поисковым прогнозом перспективы изменения состояния аварийности неблагоприятны, то необходимо предпринять действия, которые изменят существующие тенденции. Таким образом, поисковое прогнозирование проводится не для того, чтобы прогноз сбылся, а для того, чтобы оценить возможные результаты сложившейся практики, борьбы с аварийностью и при необходимости перестроить свою работу.
3. Факторный прогноз на основе построения математических зависимостей показателей аварийности от различных управляемых и неуправляемых факторов. Для построения факторной модели необходимы данные о значениях факторов в предшествующие периоды времени, а для прогноза - данные об ожидаемых значениях факторов в будущем:
   
   
   Факторный прогноз наиболее универсален с точки зрения управленческого процесса, так как позволяет оценить возможные последствия любых действий, если только они выражены в количественном виде и включены в модель в виде переменной. Неслучайно поэтому то огромное внимание, которое уделяется построению факторных моделей аварийности у нас в стране и за рубежом. Однако до сих пор ни одна из факторных моделей не получила достаточного признания и широкого применения на практике. Связано это не с недостатками проводившихся исследований, а с принципиальной невозможностью разработки модели, пригодной для всех возможных случаев и конкретных ситуаций. Действительно, можно легко согласиться с тем, что модели для прогнозирования показателей аварийности на территории республики (края, области, города) должны отличаться от моделей аварийности на транспорте министерств и ведомств, а те, в свою очередь, от моделей аварийности по автодорогам и т. д. Но даже если модель построена для конкретных условий, любая новая цифра, любое изменение условий и содержания работы по профилактике ДТП могут потребовать полного изменения используемых зависимостей. Это не говорит о ненужности или невозможности прогнозирования аварийности. Речь идет о том, что для каждой конкретной ситуации почти всегда необходимо заново решать задачу прогнозирования и получать свою индивидуальную для данных условий модель. Формальная постановка задачи построения факторной - модели выглядит следующим образом. Имеется набор значений показателя аварийности у за некоторый предшествующий период времени, а также матрица значений переменных хг, х2,. ., хП9 влияющих на этот показатель:
   
   
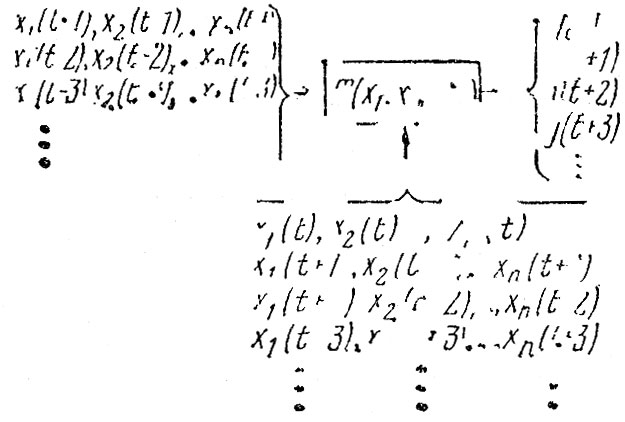   Далее делается предположение о виде зависимости y = F (а₁, a₂, ..., а_n, х₁, х₂, ..., х_n) с точностью до некоторых неизвестных параметров а₁a₂...a_k. Задача заключается в расчете этих параметров на основе имеющихся исходных данных. Вычисление параметров в зависимости от вида функции и объема исходных данных может представлять собой весьма сложную проблему. Однако мы не будем на этом подробно останавливаться, поскольку методы вычислений подробно изложены в специальных изданиях [16]. К тому же большинство из них реализованы на ЭВМ в виде стандартных программ и пользователю необходимо лишь подготовить исходные данные. Поэтому мы основное внимание сосредоточим на тех аспектах построения прогнозирующих моделей, которые зависят от человека и требуют обязательного его участия.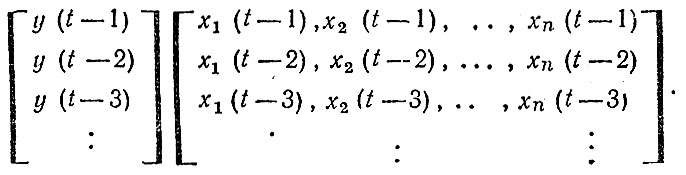

1. Выбор вида функции. Существуют два основных критерия для выбора вида функции - точность подгонки модели под существующие данные и физический смысл зависимости.

Точность подгонки моделей - легко формализуемый критерий, который может быть реализован на ЭВМ. Для этого необходимо в памяти ЭВМ хранить некоторую "библиотеку" моделей, из которой подбирается одна или несколько зависимостей, в наибольшей степени подходящие под имеющиеся исходные данные. Следует, однако, иметь в виду, что обычно можно подобрать несколько видов зависимостей, точно или приблизительно одинаково соответствующих исходным данным. Ниже приведен пример для одного показателя аварийности y и двух переменных х₁ и х₂:

Имеются два вида моделей, абсолютно точно описывающих эти данные: y = х²₁; y = х₁ + х₂.

Никакими формальными методами невозможно отдать предпочтение одной из этих функций,и только человек, учитывая физический смысл процесса, может ответить на вопрос о том, какая из зависимостей больше соответствует действительности.

Таким образом, подбор функции проводится следующим образом: ЭВМ по критерию точности готовит "предложения" о возможном виде функции, а исследователь, сообразуясь со своим опытом и знанием системы ОБДД, делает окончательный выбор. Естественно, что в процессе построения модели может оказаться, что ни одна из имеющихся в памяти ЭВМ моделей не соответствует исходным данным. Поэтому необходимо иметь возможность расширять и дополнять библиотеку моделей, хранящихся в ЭВМ.

Обычно все модели можно разделить на две большие группы: одномерные и многомерные.

Одномерные модели зависят только от одной переменной и имеют вид y = f (х). Если вместо х взять время t, то получим модель поискового прогноза y = f (t). Поэтому одномерные факторы и поисковые модели будем рассматривать одновременно.

Линейная зависимость:

Это наиболее часто используемый вид одномерной зависимости. Обычно эти уравнения называют уравнениями линейного тренда, а коэффициенты а₁ и а₂ - коэффициентами линейного тренда. Коэффициент а₁ можно трактовать как среднегодовой прирост (или снижение, если а₁<0) показателя аварийности. Таким образом, по знаку и значению a₁ можно определить основную тенденцию изменения многолетних данных (см. § 3.5).

Степенная функция:

В частном случае (при а₂ = 1) степенная функция переходит в линейную зависимость. При а₂<0 получим гиперболическое уравнение: y (х) = а₁/_x^a2.

Степенной ряд:

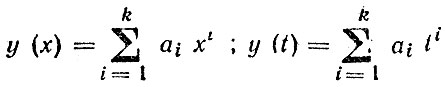
Он является обобщением линейной и степенной функций. Увеличивая степень полинома k, степенным рядом можно добиться сколь угодно большой точности модели в имеющихся точках, в том числе "провести" кривую по всем имеющимся точкам (рис. 4.8). Однако для целей прогнозирования такой излишне сложный вид функции обычно бесполезен и на практике редко используют случаи k>2.

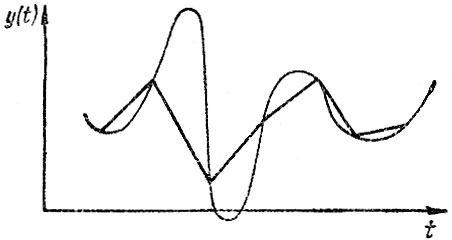
Рис. 4.8. Аппроксимация исходных данных степенным рядом

Экспоненциальная зависимость:

В результате несложных преобразований функции ее можно привести к виду:

Гиперболическое уравнение:

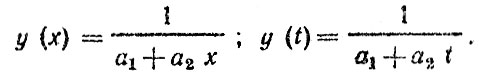
В частном случае (при а₁ = 0) оно переходит в степенную функцию.

Периодическая функция:

Наиболее часто она используется при поисковом прогнозе и позволяет учесть периодические (сезонные, суточные и др.) изменения показателя аварийности. Коэффициент а₂ задает период изменения, а₃ - фазу (сдвиг синусоиды относительно точки начала отсчета времени).

Логарифмическая функция:

Недостатком логарифмической функции является то, что она не определена при х = 0.

Рекуррентное сглаживание. Смысл процедуры заключается в том, что значение показателя последовательно вычисляется с "конца" имеющихся данных:

Например, если имеются данные за 10 лет, то сначала вычисляется показатель аварийности на период времени, отстоящий на 9 лет от текущего года, затем, используя ранее полученный результат, - на 8 лет и т. д.

Существуют многочисленные варианты рекуррентных соотношений, которые позволяют учесть специфику исходных данных. Например, если сама функция имеет периодические колебания, то коэффициенты а₁ и а₂ начинают зависеть от того, на какой период времени дается прогноз. Действительно, если мы разрабатываем прогноз на май, то значения показателей аварийности в мае за предшествующие годы должны иметь, очевидно, больший вес, чем аналогичные показатели в январе или августе.

Мы не будем дальше перечислять всевозможные одно-факторные модели. В основном они представляют собой комбинации перечисленных выше функций. При необходимости они сравнительно легко могут быть составлены самостоятельно или выбраны из известных, опубликованных в специальных изданиях [16]:

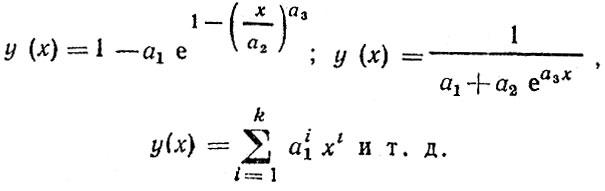
Общей теории построения многофакторных моделей не существует. Обычно многофакторные модели "составляют" из комбинации однофакторных, либо перемножая, либо суммируя их, т. е. полагая, что

или

С точки зрения технологии проведения расчетов неизвестных параметров эти функции не имеют принципиальных различий, так как вторая сводится к первой логарифмированием:

Если каждая из функций f_i (x_i) - линейная, то получим хорошо изученное линейное уравнение множественной регрессии:

Если каждая из функций φ_n (x_n) - степенная, то придем к обобщению формулы, полученной Р. Смидом [311:

Большой популярностью для решения конкретных задач прогнозирования пользуется метод группового учета аргументов (МГУА). Он основан на принципах направленного перебора, когда полное описание процесса y = F (x₁, х₂, ..., х_n) заменяется иерархической системой частных описаний:

1-й ряд: y₁ = f (x₁, х₂); y₂ = f (x₁, x₃); ... y_m = f (x_i, x_j);

2-й ряд: z₁ = f (y₁, y₂); z₂ = f (y₁, y₃); ... z_m = f (y_i, y_j); и т. д.

На каждом уровне иерархии (на каждом ряду) по определенному критерию (например, минимуму ошибки) отбирается некоторое число зависимостей, в наилучшей степени соответствующих исходным данным. Основным достоинством метода МГУА является то, что на каком-то ряду увеличение сложности модели перестает повышать степень приближения к исходным данным. Таким образом, метод имеет свойства самоорганизации, адаптации к сложности моделируемого процесса [16].

2. Выбор исходных данных. Выбор исходных данных определяется несколькими обстоятельствами, оказывающими противоположное влияние на состав и объем исходных показателей.

С точки зрения точности прогнозируемых результатов мы должны включить в модель как можно большее число показателей, влияющих на состояние аварийности. Если мы исключим из модели ту или иную переменную, то ее воздействие на состояние аварийности будет восприниматься как неточность прогноза и увеличивать доверительный интервал возможностей ошибки.

С другой стороны, использование большого числа факторов ограничивается возможностями методов оценки параметров. В частности, число исходных данных не может быть меньше числа оцениваемых параметров. Например, в простейшей линейной многофакторной модели число параметров равно k + 1, где k - число факторов, включенных в модель. Следовательно, если мы хотим составить модель для прогнозирования аварийности по 30 факторам, то нам необходимы данные за 31 год по всем 30 факторам и о показателе аварийности.

Практикой выработано несколько путей выхода из подобного противоречия.

Во-первых, можно действительно увеличить анализируемый интервал времени. Однако следует иметь в виду, что при этом мы полагаем неизменным вид модели на весь этот период времени. При воздействии многих факторов это предположение может оказаться неверным. В частности, изменение Правил учета ДТП может приводить к значительной неоднородности значений самого прогнозируемого показателя аварийности.

Во-вторых, для построения модели можно использовать данные не по одной республике, краю, области, а по группе схожих между собой регионов. Схожие между собой регионы можно выделить, например, методами таксономии.

В-третьих, можно среди различных признаков отобрать наиболее информативные. Действительно, опыт показывает, что не все факторы одинаково важны для построения модели. Часть из них может быть исключена из модели без существенной потери точности прогноза. Выделить информативные признаки можно, например, методом главных компонент, основная идея которого описана в § 4.6.

Четвертый путь сокращения объема исходных данных - построение обобщенных факторов на основе исходных. Так же, как и методы таксономии и главных компонент, факторный анализ относится к группе многомерных методов обработки исходных данных.

На выбор исходных показателей, которые предполагается включить в модель, могут оказать существенное влияние и такие "прагматические" обстоятельства, как стоимость сбора сведений и их достоверность. Некоторые факторы (например, число водителей, управляющих транспортными средствами в нетрезвом состоянии, но не совершивших ДТП) могли бы оказать существенное влияние на вид модели, но сбор сведений о них потребовал бы чрезвычайно больших затрат, Другие переменные (например,прогноз погоды) имеют низкую достоверность и поэтому также не могут быть включены в модель.

3. Период и точность прогнозирования. Относительно точности прогноза поисковых моделей мы уже отмечали, что они делаются в предположении, что существующие тенденции сохранятся. На основе этих предположений можно строить в принципе прогноз на сколь угодно отдаленный период. Однако на практике поисковые прогнозы бывают краткосрочными - на период до одного года. В редких случаях при наличии многолетних устойчивых тенденций может быть сделана оценка на 5-10 лет вперед.

О точности факторных моделей можно говорить только в интервале значений переменных x₁...x_n, которые встречались при построении моделей. Если же прогноз делается для значений переменных, которые в исходных данных при построении моделей не встречались, то, как и при поисковом прогнозе, должно быть сделано предположение о том, что установленные закономерности сохраняются и для новых значений х.

Одна из наиболее распространенных ошибок при использовании прогностических моделей - игнорирование взаимосвязи используемых факторов. Например, во многих регионах страны существует устойчивая взаимосвязь между протяженностью дорог с твердым покрытием и числом легковых автомобилей индивидуальных владельцев. Если мы будем использовать прогностическую модель, в которую включены эти факторы, в предположении, что протяженность дорог возрастет, а численность автомобилей не изменится, то мы допустим серьезную неточность в прогнозе. В общем случае при прогнозировании необходимо решить систему уравнений:

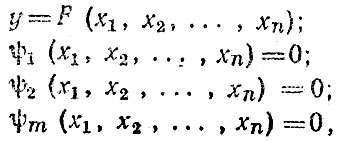
где ψ_j (x₁, x₂, ..., x_n) = 0 - уравнения, описывающие взаимозависимость факторов и накладывающие ограничения на их изменение.

Следует отметить, что любые виды прогностических моделей строятся на основе статистических данных, поэтому и точность прогноза имеет вид статистического вывода: указываются доверительный интервал и доверительная вероятность.

4. Цель прогноза и предшествующий опыт. Цель, с которой ведется анализ и прогнозирование, не может не оказывать влияния на построение модели. Например, если мы прогнозируем состояние аварийности на индивидуальном транспорте, то нас вряд ли будет интересовать охват водителей предрейсовым и послерейсовым осмотром на автотранспортных предприятиях. В ряде случаев нас может устраивать сравнительно небольшая точность, в других - нужны более надежные результаты. Поскольку аналитические результаты гораздо легче использовать, если модели имеют сравнительно простую форму, то часто стараются ограничиться линейными моделями. Однако в некоторых случаях нас могут интересовать только результаты, полученные по принципу вход - выход без разъяснения промежуточных расчетов. Существуют и другие обстоятельства, которые воздействуют на процесс моделирования.

Следует однако иметь в виду, что цель не должна воздействовать на достоверность выводов. На рис. 4.9 изображены три альтернативные кривые, которые с приблизительно одинаковой точностью отражают имеющиеся данные. Однако прогнозы по этим моделям принципиально отличаются друг от друга. Только тщательное обоснование,установление механизма причинно-следственных связей между у и сможет позволить исследователю выбрать ту или иную модель. В противном случае можно сознательно или бессознательно "подогнать" модель под желательный прогноз.

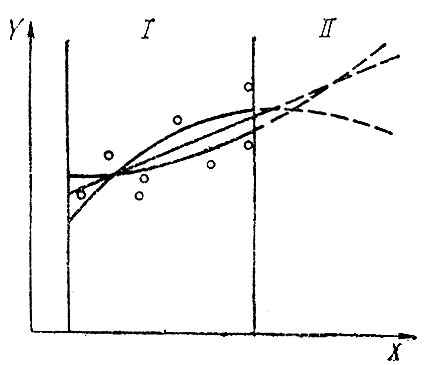
Рис. 4.9. Альтернативные модели по одним и тем же исходным данным: I - область исходных данных; II - область прогноза

Важную роль в построении модели может играть предшествующий опыт, ранее выявленные закономерности. С одной стороны, и это мы уже отмечали, любые новые данные могут потребовать пересмотра полученных ранее соотношений и построения новых моделей. С другой стороны, не следует игнорировать предшествующий опыт. Если изменилась существовавшая ранее закономерность, если необходимо изменить ранее разработанную модель, то это, очевидно, обусловлено какими-то причинами. До тех пор, пока эти причины не установлены и изменение закономерностей не объяснено, необходимо особенно осторожно подходить к новым моделям.

Подытоживая сказанное, можно утверждать, что процесс разработки модели и подготовки прогноза состояния аварийности представляет собой человеко-машинную процедуру, в которой функции человека дополняются возможностями ЭВМ. При этом на ЭВМ в основном возлагаются все "формальные обязанности" по проведению необходимых расчетов, а на человека - содержательная работа по подготовке исходных данных, интерпретации и объяснению полученных формальными методами результатов.

Таблица 4.10. Процесс разработки многофакторной модели прогнозирования

Основные функции человека и возможности ЭВМ при построении многофакторных моделей перечислены в табл. 4.10.