§ 4.6. Факторный анализ

Факторный анализ зародился и впервые стал применяться в психологии при обработке данных, полученных в результате проведения тестов по выявлению умственных способностей личности. Затем он получил весьма широкое развитие и распространение в других областях исследований, в том числе и в сфере ОБДД.

Принято считать, что на состояние аварийности влияют дорожные условия, дисциплина участников дорожного движения, активная и пассивная безопасность конструкций транспортных средств и другие факторы. Однако каковы значения этих факторов, где и в каких условиях их влияние сказывается больше, а где меньше, мы, как правило, ответить не можем. Для нахождения ответов на эти вопросы и применяются методы факторного анализа.

Сущность факторного анализа заключается в выявлении фактора, не поддающегося непосредственному измерению и проявляющегося в ряде косвенных показателей. Факторы должны быть по возможности простыми и достаточно точно описывать и объяснять наблюдаемые величины. Как правило, число выделяемых факторов должно быть существенно меньше числа исходных показателей.

Методологической основой постановки и решения этой задачи является предположение о том, что если такие факторы существуют и воздействуют на какие-то переменные, то между этими переменными должна существовать взаимосвязь, поскольку изменения каждой из переменных зависят от изменения одного и того же фактора (рис. 4.10). Таким образом остается выделить группу взаимосвязанных между собой исходных показателей и попробовать установить, какой фактор обусловливает их взаимосвязь.

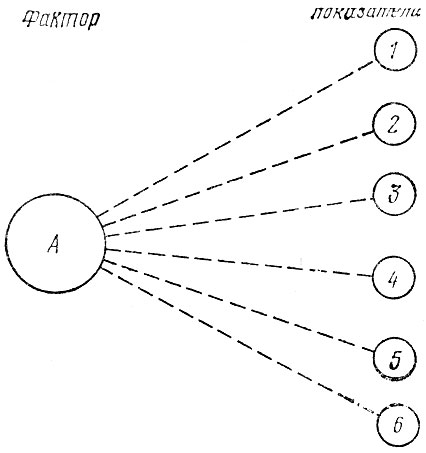
Рис. 4.10. 'Взаимосвязь показателей с одним фактором

Например, изучение статистических данных о ДТП в республиках, краях, областях страны показало наличие тесной взаимосвязи между долями происшествий, возникших в результате следующих шести видов нарушений Правил дорожного движения водителями: превышение скорости в опасных условиях; нарушение правил обгона; несоблюдение очередности проезда; внезапный выезд на левую сторону движения; неправильный выбор и несоблюдение дистанции; нарушение рядности и правил маневрирования.

Из характера допущенных нарушений можно предположить, что все они являются следствием неопытности и недостаточной квалификации водителей. Использование методов факторного анализа позволяет установить связь между исходными показателями и фактором неопыт ности и количественно выразить значение этого фактора для каждой республики, края, области. Исходя из этого значения можно планировать мероприятия , осуществлять целенаправленный управленческий процесс улучшения подготовки и повышения квалификации водителей .

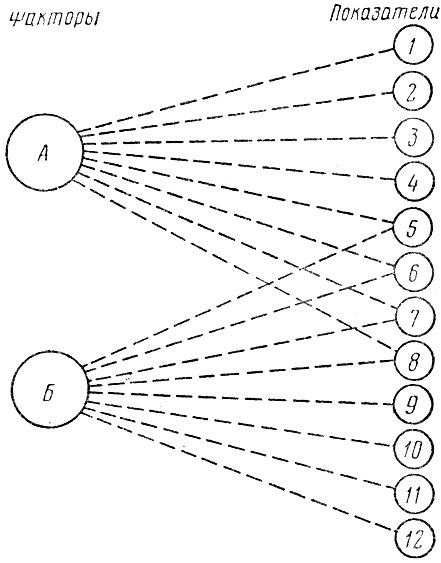
Рис. 4.11. Взаимосвязь показателей с двумя факторами

К сожалению, не всегда взаимосвязь обнаруживается и объясняется так просто. Как правило, в системе ОБДД на одни и те же показатели влияют несколько неизмеряемых, скрытых факторов. В этом случае на изменение показателей в результате воздействия одного фактора накладываются воздействия другого и взаимосвязь показателей перестает носить явный характер. На рис. 4.11 изображено воздействие двух факторов А и Б на 12 показателей, из которых четыре (5, 6, 7 и 8) зависят и от А и от Б. Если в результате воздействия фактора А измеряемые показатели возрастают, а в результате воздействия фактора Б - снижаются, то первые четыре показателя увеличатся, последние четыре - сократятся, а значения показателей 5-8 могут или возрасти или снизиться. Установление связи этих показателей между собой, с другими показателями и с самими факторами представляет собой весьма непростую задачу, требующую огромного объема вычислений.

Задача проведения необходимых вычислений значительно усложняется, если сами факторы зависят от еще более общих факторов, т. е. появляется своеобразная иерархия взаимозависимостей. На рис. 4.12 изображены два уровня факторов, воздействующих на показатели. Очевидно, что характер взаимозависимости исходных показателей в этом случае становится еще более запутанным.

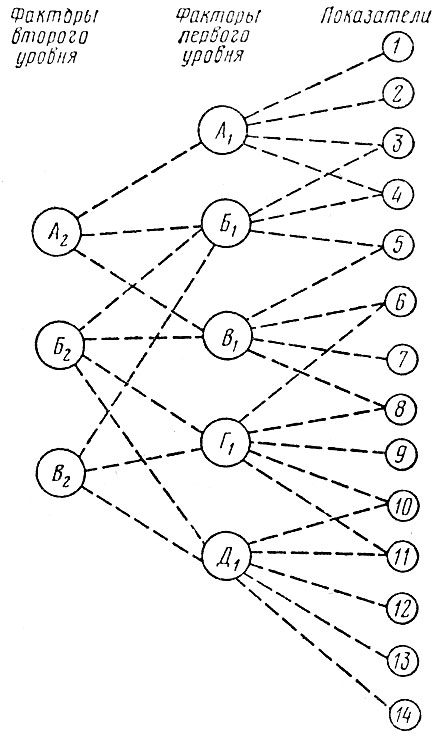
Рис. 4.12. Многоуровневая взаимосвязь показателей и факторов

Сложность математического аппарата, требующего знания теории вероятности, математической статистики и линейной алгебры не должна смущать пользователей. Развитие средств вычислительной техники в значительной мере снижает указанные трудности, поскольку в стандартном математическом обеспечении большинства современных ЭВМ имеются программы, реализующие методы факторного анализа. Более того, использование этих программ создает даже иллюзию "легкости" проведения анализа без глубокого понимания сущности используемых процедур и получаемых результатов. Однако формальное использование методов факторного анализа без профессионального знания сущности моделируемого процесса - функционирования системы ОБДД может привести к необоснованным выводам и заключениям. Поэтому главным действующим лицом при проведении факторного анализа должен быть специалист (или группа специалистов), который выдвигает гипотезы о наличии и сущности факторов и интерпретирует результаты расчетов. Непосредственное же проведение вычислений представляет собой при условии использования ЭВМ рядовую расчетную задачу.

В формализованном виде процедуру подготовки и проведения факторного анализа можно представить в виде нескольких последовательно выполняемых этапов.

1. Формулировка цели проводимого факторного анализа. На основе методов факторного анализа можно решить по крайней мере следующие четыре задачи:

• нахождение и количественное измерение скрытых, но объективно существующих факторов, которые проявляются в ряде измеряемых показателей;
• выявление и изучение связи исходных показателей с факторами для выработки научно обоснованных управляющих решений, способных более эффективно воздействовать на состояние аварийности;
• сжатие информации в результате описания процесса не многочисленными исходными показателями, а меньшим числом выделенных факторов;
• прогнозирование уровня аварийности на основе уравнений регрессии, где в качестве переменных выступают обобщенные факторы; построенные таким образом регрессионные уравнения имеют значительные преимущества перед классическим регрессионным анализом, в модели которого включаются исходные показатели.

2. Отбор показателей для проведения факторного анализа. Выбор показателей определяется целью факторного анализа.

Если изучается структура малоизученного явления, то необходимо привлекать как можно более разнообразные исходные переменные, которые всесторонне характеризуют область исследования.

Если же существует гипотеза относительного содержания фактора и состава показателей, на которые этот фактор воздействует, то для проверки правильности выдвинутой гипотезы можно использовать ограниченный набор показателей.

Особое внимание следует уделить качеству исходных данных. Ошибки, допущенные при измерениях, переписке и при вводе данных в ЭВМ, могут существенно изменить конечные результаты и выводы.

Обычно исходные данные представляются, как и при регрессионном анализе, в виде матрицы

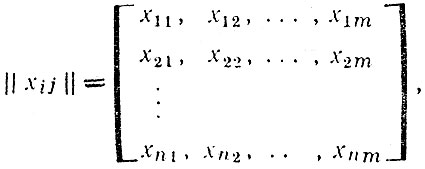
где каждый столбец означает новую переменную, а каждая строка - значения исходных показателей для разных объектов. В зависимости от целей анализа под объектами могут пониматься различные автотранспортные предприятия, районы, города, области и т. д. Это может быть один и тот же объект, для которого значения показателей фиксируются в разные моменты времени.

Важной характеристикой матрицы хи является разброс переменных относительно их среднего значения количественно описываемой величиной:

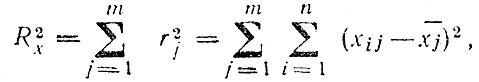
где 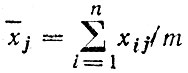- среднее значение каждой переменной.

3. Техническое осуществление факторного анализа. Формальная сторона факторного анализа состоит в том, что на основе матрицы ||x_ij|| определяется система уравнений:

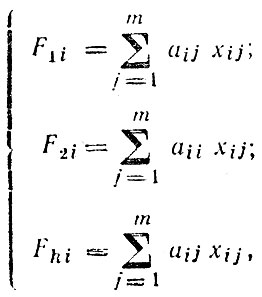
где F₁,..., F_k - факторы, влияющие на исходные показатели x_ij, причем k (число факторов), как мы уже отмечали, должно быть значительно меньше m (число переменных); a_ij - постоянные коэффициенты, называемые факторной нагрузкой.

Подставив в эту систему уравнений исходные значения, получим матрицу ||F_ij||:

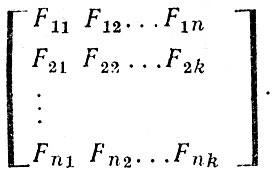
Как и для матрицы ||x_ij|| для ||F_ij|| можно вычислить R_F:

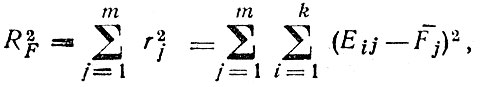
где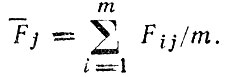

Коэффициенты а_ij рассчитывают на ЭВМ при помощи специальных методов таким образом, чтобы RF как можно меньше отличалась от R²_F. В этом состоит основная "техническая" цель факторного анализа, который стремится при помощи минимально возможного числа факторов объяснить различие (разброс) исходных показателей.

В "классическом" факторном анализе исследователю необходимо сформулировать гипотезу о наличии фактора и о составе тех переменных, на которые этот фактор оказывает влияние. С помощью же формальных методов проводится только расчет коэффициентов a_ij.

Имеется видоизмененный вариант факторного анализа, который называется методом главных компонент [I1J. Этот метод позволяет не только найти коэффициенты а_ij, но и подобрать переменные таким образом, чтобы новый фактор в максимальной степени объяснял различие в значениях исходных показателей. Затем подбирается второй фактор таким образом, чтобы он максимально объяснял оставшийся разброс значений показателей и т. д. В отличие от факторного анализа метод главных компонент сам формирует факторы, но при этом не гарантируется, что этот фактор будет иметь какое-либо смысловое значение. Задача содержательной интерпретации полученных главных компонент и обоснования их как объективно существующих факторов остается функцией человека.

Интерпретация факторов. Факторный анализ и метод главных комнонент являются сугубо количественными методами и формально позволяют получить результат (выделить факторы) практически при любом составе исходных показателей независимо от того, существует объективно этот фактор или нет. Обоснование существования этого фактора, интерпретация полученных результатов носят в значительной мере качественный характер. Если выделенные факторы не носят очевидный содержательный характер, то нередко даже специалистов в области факторного анализа не удается убедить в справедливости полученных выводов и в необходимости их использования в практической управленческой деятельности.

Конечные результаты факторного анализа в значительной мере зависят от выбора исходных переменных, конкретной модификации применяемого метода, опыта и квалификации исследователя и других обстоятельств субъективного характера. В подобной субъективности нет ничего предосудительного, поскольку при анализе данных субъективные суждения используются довольно часто. Однако надо иметь четкое и ясное представление о том, что методы, имеющие в некоторой степени произвольный характер, сами по себе не могут служить средством обоснования объективного существования каких-либо факторов. В конечном итоге только исследователь, хорошо изучивший и знающий проблему ОБДД, может делать выводы по результатам, полученным методами факторного анализа.

Следует отметить, что многомерные методы анализа не исчерпываются факторным анализом и методом главных компонент. Существует ряд других методов, более или менее тесно связанных с факторным анализом. Среди них можно выделить множественный регрессионный, дисперсионный, дискриминантный и кластерный методы анализа, а также методы распознавания образов.

Дисперсионный анализ. По содержанию получаемых результатов дисперсионный анализ ближе всего подходит к регрессионному анализу, поскольку изучает влияние одного или нескольких факторов на один или несколько результирующих показателей, значения и содержание которых заведомо известны. Таким образом, дисперсионный анализ не позволяет выделить неизвестные факторы или проверить гипотезу об их существовании. При конкретных исследованиях можно комбинировать дисперсионный анализ с факторным. Вначале, когда структура и наличие факторов еще неизвестны, полезно применить методы факторного анализа. Затем можно провести дисперсионный анализ чтобы доказать влияние факторов на результирущие показатели.

Дискриминантный анализ. Этот анализ является одной из разновидностей факторного анализа, когда на основе матрицы ||x_ij|| все объекты необходимо разделить на две и большее число групп, причем характеристики каждой группы уже известны. Например, такого рода задача возникает, если x_ij - значения показателей аварийности, и необходимо республики, края и области разделить на две группы, имеющие высокий и низкий уровень аварийности В отличие от факторного анализа, где проводится группировка столбцов матрицы ||x_ij||, в дискриминантном анализе аналогичная процедура проводится со строками.

В первоначальном варианте задача дискриминантного анализа сводится к поиску ответа на вопрос: отличаются ли две совокупности объектов одна от другой или они должны быть отнесены к одной группе?

Кластерный анализ. В отличие от дискриминатного в кластерном анализе заранее не задаются классы объектов и их свойства. Разбиение объектов на группы проводится автоматически по некоторому критерию. При этом число классов может заранее фиксироваться, либо определяться в процессе расчетов.

Основная трудность реализации кластерного анализа заключается в выборе и обосновании критерия, который позволял бы оценивать качество того или иного разбиения на классы.

Все предложенные критерии так или иначе сводятся к оценке расстояния между объектами в одной группе и между группами объектов в многомерном пространстве исходных переменных. При этом все критерии дают приблизительно одинаковый результат, если имеются четко выраженные, удаленные друг от друга группы объектов. При отсутствии четкой структуры в делении объектов на группы ни один из критериев не дает удовлетворительного результата и остается неясным, является ли найденное разбиение действительно единственным и наилучшим и соответствует ли оно какому-либо объективному критерию.

Методы распознавания образов. Постановка задачи и результат решения методом распознавания образов тесно связаны с дискриминантным и кластерным анализами. В классической постановке методы распознавания образов предполагают априорное знание классов, к которым относится каждая строка матрицы ||x_ij||. На этой основе решающие правила строятся таким образом, чтобы произвольную строку матрицы они относили к тому или иному классу с минимальным числом ошибок.

Основная трудность здесь состоит в поиске типа решающих правил и доказательства того факта, что полученные решающие правила в данной задаче действительно дают минимальное число ошибок.

Для решения этих задач обычно всю совокупность строк делят на обучающую и контрольную выборки. По обучающей выборке осуществляется построение решающих правил, а по контрольной - оценка числа ошибок (в последнее время методы распознавания образов стали находить полезное применение при больших массивах статистических данных).

Факторный анализ совместно с другими методами многомерного анализа позволяет создать комплексную модель исследуемого явления, открыть новые возможности в постановке и решении задач ОБДД, особенно при анализе большого числа показателей. Один из примеров такого анализа можно найти в [11]. Исследовалась структура дорожно-транспортной аварийности в республиках, краях и областях РСФСР. Исходная матрица содержала ПО столбцов - параметров, имеющихся в карточке учета ДТП, и 69 строк - по числу объектов административно-территориального деления РСФСР. Факторный анализ этой матрицы позволил выявить три фактора, влияющих на структуру дорожно-транспортной аварийности: скоростной потенциал транспорта, скоростной потенциал (качество) дорожной сети, интенсивность пешеходного движения. На основе выявленных факторов осуществлено разбиение регионов РСФСР на однотипные группы, что позволяет конкретизировать управленческий процесс, более целенаправленно планировать и проводить мероприятия по предупреждению ДТП, воздействуя в каждой группе регионов на свой, оказывающий более заметное влияние на структуру аварийности, фактор.