1.2. Анализ методов расчета показателей надежности механических систем

Методы расчета показателей надежности могут быть разделены на три группы: расчет ресурса элементов деталей или модели отказов элементов; расчет ресурса деталей, включающих несколько элементов, или модели отказа деталей; расчет показателей надежности агрегатов автомобиля как сложных восстанавливаемых систем.

Следует заметить, что иногда отождествляются понятия модели отказа элемента детали и модели отказа детали. Это справедливо в том случае, если у данной детали наблюдается один преобладающий вид отказа, например износ накладок сцепления, усталостное выкрашивание зубьев шестерен и т. п. Но для большинства деталей механических систем характерно одновременное протекание нескольких разрушительных процессов. В этом случае для каждого разрушительного процесса можно воспользоваться соответствующей моделью расчета ресурса элемента детали, тогда как для детали необходимо разработать модель отказа, которая включает элементарные модели расчета. Например, первичный вал коробки передач (рис. 1.3) может выйти из строя вследствие износа шлицев под ведомый диск сцепления, выкрашивания зубьев шестерни, износа торцев зубьев каретки синхронизатора и др. В табл. 1.5 приведены дефекты элементов первичного вала, наблюдающиеся в эксплуатации и при капитальном ремонте, и указаны виды расчета, соответствующие этим дефектам. Из таблицы следует, что для формирования расчетной модели ресурса первичного вала необходимо описать 10 процессов для его элементов, 6 из которых связаны с износами, 2 - с прочностью и 2 - с усталостью.

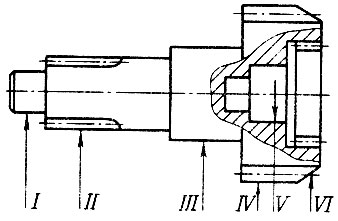
Рис. 1.3. Эскиз первичного вала коробки передач: I- VI - элементы вала

В соответствии с п. 1.1 основными причинами отказов и неисправностей деталей автомобиля являются износы, усталостные и прочностные поломки" В теории и практике оценки ресурсов элементов получили развитие соответствующие расчетные модели, например случайный процесс - поле допуска (расчет на износ), гипотеза суммирования повреждений (расчет на усталость)" Рассмотрим подробнее основные зависимости.

Методы расчета на износ

Методы расчета на износ условно могут быть разделены на аналитические и экспериментальные.

Таблица 1.5. Основные дефекты и виды расчета элементов первичного вала коробки передач

Под аналитическими понимают методы, которые позволяют оценить износ детали (сопряжения) на этапах проектирования без экспериментальных замеров.

В Методике расчетной оценки износостойкости поверхностей трения деталей машин [43] даны аналитические зависимости для интенсивностей изнашивания при упругом

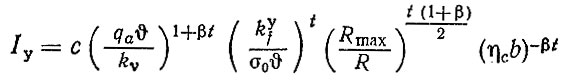(1.1)

и при пластическом контактах

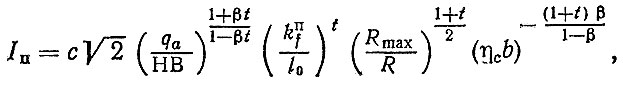(1.2)

где

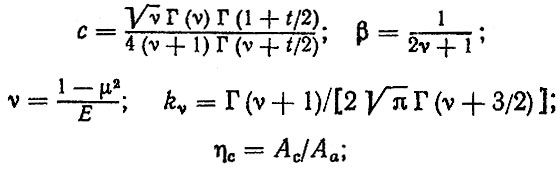
q_a - номинальное давление; θ - постоянная упругости истираемого материала; μ - модуль упругости; Е - коэффициент Пуассона; R - средний радиус кривизны вершин микронеровностей; σ₀, t_у, t₀, t_п - константы фрикционной усталости истираемого материала [в формулах (1.1), (1.2) для удобства записи индексы при t опущены]; k_j<>^y/sub> коэффициент, зависящий от пределов прочности при растяжении и сжатии материала и коэффициента трения f; R_max - максимальная высота неровностей поверхности; A_с, А_а - контурная и номинальная площади контакта; b, ν - параметры степенной аппроксимации начального участка опорной кривой; НВ - твердость по Бринеллю; k^п_f - коэффициент, зависящий от предела текучести; Г ( ) - гамма- функция.

Вывод формул (1.1), (1.2) основан на гипотезе фрикционной усталости, впервые предложенной И. В. Крагельским. В соответствии с основной расчетной схемой рассматривается изнашивание в стационарном (установившемся) режиме сухого или граничного трения; методика не может быть применена для расчета сопряжений, работающих в жидкостном или смешанном режиме трения. Сопоставление расчетных I_ри средних экспериментальных I (из десяти значений) интенсивностей изнашивания в большом диапазоне варьирования исходных параметров показало, что с вероятностью Р ≥ 0,9 наблюдается соотношение 0,4Ii≤I_p≤2,6I [32].

Широкий интервал вероятных значений средних интенсивностей изнашивания ограничивает возможности использования формул (1.1), (1.2) для оценки абсолютных значений износов и ресурса, но расчетные значения успешно могут быть применены для получения сравнительных оценок различных пар трения для проектируемого узла. Очевидно, дальнейшее развитие усталостной теории износа и совершенствование информационной базы позволят повысить точность расчета и эффективно управлять процессом износа.

При исследовании механических систем большое распространение получили методы, основанные на непосредственных замерах износов в функции от времени (экспериментальные методы). В этом случае износ является интегральным показателем, объединяющим множество факторов, включая и условия эксплуатации машины"

Известно, что основными показателями износа являются: линейный износ и, мкм; скорость изнашивания γ = du/dt, мкм/ч; интенсивность изнашивания j = du/ds, где S - относительный путь трения, на котором происходит изнашивание. При исследованиях износа деталей автомобилей под интенсивностью изнашивания часто понимается величина m_и = du/dLy где L - наработка автомобиля в километрах пробега.

В общем случае кривая зависимости износа от времени состоит из трех участков: при работки, когда γ монотонно убывает; установившегося износа при γ = const; катастрофического износа, когда γ возрастает. Для различных сопряжений и условий изнашивания наблюдаются отклонения от общей кривой износа как по числу участков, так и по скорости изнашивания γ на этих участках.

В зависимости от исходной информации экспериментальные методы определения износа от времени можно разделить на две группы: первая, когда данные об износах u_i при соответствующих наработках t_i представляются в виде независимых пар значений u_i - t_i; вторая, когда рассматриваются реализации случайных процессов износа от времени.

Для аналитического описания износов (первая группа) используются различные зависимости: полиномы различных порядков, степенные и экспоненциальные функции. Так, при исследовании износов деталей двигателей используются полиномы вида

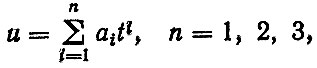(1.3)

которые позволяют описать различные зависимости износов от линейной u = a₁t, соответствующей только второму участку кривой, до кубической параболы, охватывающей три участка кривой износа.

В ряде работ приводятся зависимости, охватывающие второй и третий участки общей кривой износа. Например, для износов, зазоров, а также изменения некоторых параметров тракторов, автомобилей и др. рекомендуется использовать степенную зависимость [46]

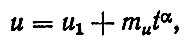(1.4)

где u₁ - детерминированное значение показателя приработки m_u - среднее значение скорости изменения параметра; α - коэффициент, α = 0,5÷2,0

Для определения среднего ресурса T_ср и коэффициента вариации v_T при заданном u_п используются формулы

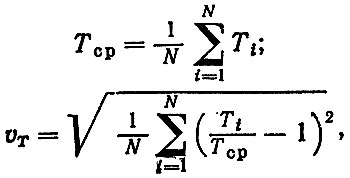(1.5)

где 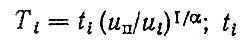- наработка i-го элемента, в течение которой показатель достиг значения u_i.

В результате обработки износов деталей быстроходных дизелей, а также шлицевых, шарнирных и других узлов трения самолетов [33] была предложена экспоненциальная зависимость

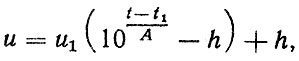(1.6)

где %- случайная величина износа при наработке t₁(I) после приработки; A, h - коэффициенты.

Определение среднего и минимального ресурсов производится по формулам!

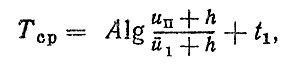(1.7)

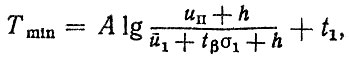(1.8)

где u^-₁, σ₁ - среднее и среднее квадратическое значения износа при наработке t₁ (после приработки); t_β - коэффициент Стьюдента [8 3.]

К недостаткам приведенных зависимостей относится то, что они не позволяют найти плотности распределения ресурсов и ограничиваются средними значениями. При нахождении других параметров v_T или Т_min на реализации процессов налагаются ограничения; вводится детерминированное значение u₁ вместо случайного; при определении коэффициентов А и h сечения процесса должны подчиняться нормальному закону.

Вторая группа методов оценки ресурса основана на том, что реализации износа элементов деталей механических систем пред" составляют собой нестационарные случайные процессы. Каждое сечение такого процесса описывается с помощью функции F (u, t) или плотности распределения f(u, t), где u - случайная величина износа. Полагают, что они могут быть отнесены к случайным процессам со слабым перемешиванием, а отдельные реализации аппроксимированы линейными или нелинейными зависимостями. Так, в работе [20] реализации износа описываются линейными зависимостями (веерная функция)

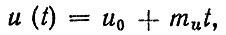(1.9)

где u₀ - детерминированная величина (полюс); m_u - случайная величина скорости изнашивания, подчиняющаяся нормальному закону распределения.

Использование теоремы о преобразовании случайных величин [8] при достижении линейными реализациями предельного значения u_п позволило найти плотность распределения ресурса f(t) в виде α-распределения (рис. 1.4, а)

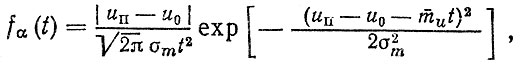(1.10)

гдеm^-_u , σ_m - среднее значение и среднее квадратическое отклонение скорости изнашивания.

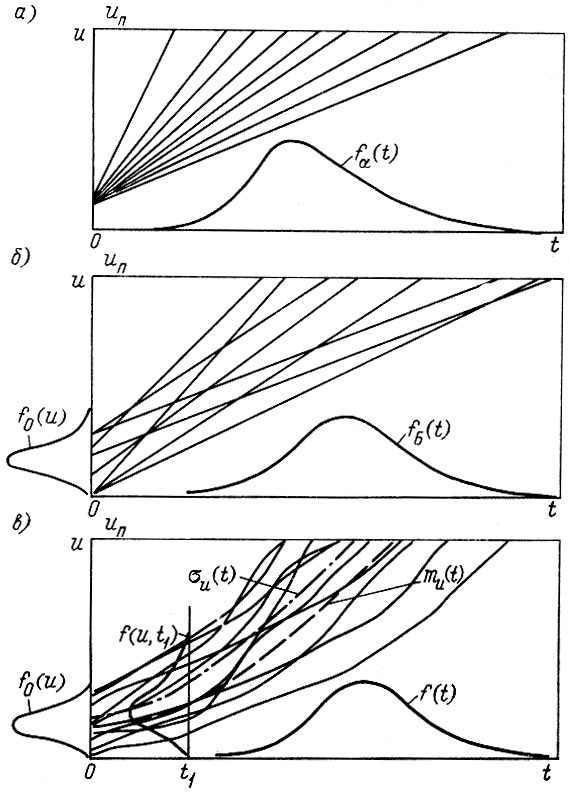
Рис. 1. 4. Определение плотности распределения ресурса по износу: а - f_α(t) - α-распределение; б - f_Б(t) - распределение Бернштейна; в - модель 'случайный процесс - поле допуска'

Если случайные величины u₀и m_u, входящие в формулу (1.9), независимые и подчиняются нормальным законам распределения, то для плотности распределения ресурса f (/) на основе вероятностного перехода было получено дисперсионное распределение Бернштейна [12] (рис. 1.4, б).

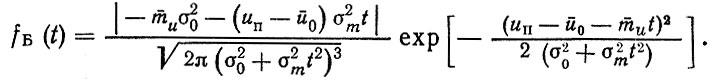(1.11)

Однако при наличии более сложных зависимостей, описываю перехода или теоремы о преобразовании случайных величин затруднено.

Другой метод определения плотности распределения f (t) заключается в том, что для случайных процессов (рис. 1.4, в) с монотонно изменяющимися моментами функции распределения F (u, t), в частности, с математическим ожиданием m_u (t) и средним квадратическим отклонением σu (t), плотность распределения, описывающая пересечение реализациями процесса односторонней границы, u_п записывается в виде

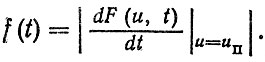(1.12)

Знак |u =u_п в формуле (1.12) означает, что после операции дифференцирования в полученную формулу вместо и подставляется u_п. Модель (1.12) получила название "случайный процесс - поле допуска" [45].

Дальнейшее совершенствование методов расчета ресурса на износ требует обобщения различных подходов, а также систематизации данных о кривых износа и скоростях (интенсивностях) изнашивания.

Методы расчетов на усталость

Изучению природы усталостного разрушения посвящено много исследований, "но ни одна из существующих теорий не дает возможности объяснить всю совокупность закономерностей, наблюдающихся при многоцикловом усталостном разрушении металлов" 158, с. 551. Поэтому практические расчеты на усталостную долговечность элементов механических систем основываются на феноменологической гипотезе суммирования (накопления) усталостных повреждений, которая позволяет по кривым усталости, полученным при испытании деталей на стендах, судить об их ресурсах в соответствующих условиях эксплуатации, представленных в расчетах схематизированными нагрузочными режимами (рис. 1.5).

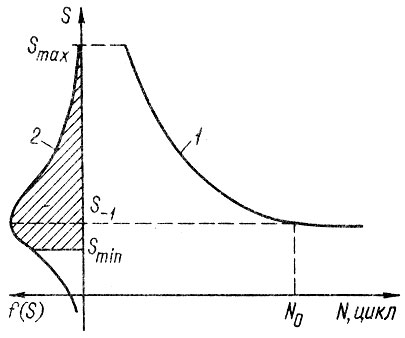
Рис. 1.5, Составляющие модели расчета на усталость по линейной гипотезе суммирования повреждений (ЛГСП): 1 - кривая усталости N (S); 2 - плотность распределения нагрузочного режима

Гипотеза основана на предположении, что повреждение, вы-званное циклом напряжений, не зависит от состояния детали в данный момент и от предыдущей истории нагружения и просто суммируется с повреждениями, вызванными предыдущими циклами. При непрерывном изменении напряжений соответствующих эксплуатационным режимам нагружения, основная расчетная формула записывается в виде

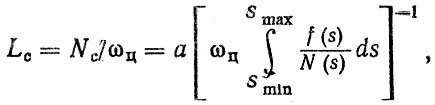(1.13)

где L_с - ресурс элемента (детали); N_c - общее число циклов до разрушения; f(S) - плотность распределения амплитуд напряжений S; N(S) - уравнение кривой усталости; S_min, S_max - область напряжений, активно участвующих в накоплении усталостного повреждения; соц - среднее число циклов нагружения в единицу времени; а - величина, зависящая от материала детали и условий нагружения.

В линейном варианте гипотезы а = 1, S_min = S_-1 где S_-1 - предел усталости. Фактически гипотеза суммирования повреждений была сформулирована для гармонического процесса нагружения с симметричным циклом, у которого значения максимальных напряжений и амплитуд равны, а частота нагружения не принимается во внимание.

Исследования, проведенные при программном и случайном нагружении, показали, что циклы с амплитудами, меньшими предела выносливости" также участвуют в накоплении усталостного повреждения. Снижение нижнего предела S_min в формуле (1.13) до значений kS_-1 где k = 0,4×0,7, означает, что кривая усталости продолжена за предел выносливости S_-1.

Гипотеза получила развитие в работе [30] под названием "корректированной". Корректировка заключается в том, что в формуле (1ЛЗ) вместо а вводится коэффициент а_р величина которого зависит от вида программного блока нагружения [30]. При непрерывном спектре нагрузок f(S)

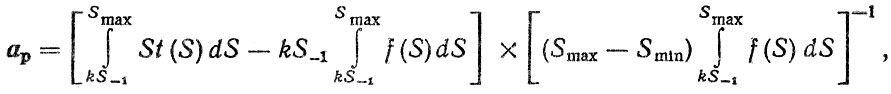(1.14)

где k = 0,6.

При а_р ≤ 0,1 рекомендуется принимать а_р = 0,1.

Для оценки точности вариантов гипотезы по результатам программных испытаний на вероятностную бумагу логарифмически нормального закона были нанесены распределения величин 1/а и а_р/а, которые характеризуют погрешности расчета для линейного и корректированного вариантов (рис. 1.6). Из рис. 1.6 видно, что использование корректирующего коэффициента ар позволяет получить на множестве всех результатов расчетов точное значение медианного ресурса (соответствующего вероятности Р = 0,5), тогда как при расчете по первому варианту результаты в среднем оказываются завышенными в два раза; с вероятностью Р = 0,95 погрешность корректированного варианта составляет 250%, а для первого варианта - 500% и более [30].

С целью уточнения зависимости (1.14) были проведены расчеты по данным программных испытаний, приведенных в специальной литературе, при этом использовались только те результаты, в которых число ступеней в блоке было не меньше трех с обязательным условием наличия ступеней с амплитудами S_min ≤ S_-1. Полученная эмпирическая функция распределения значений a_p/a при нанесении на логарифмически нормальную бумагу оказалась смещенной относительно единицы. Для нормирования данного смещения была подобрана корреляционная зависимость

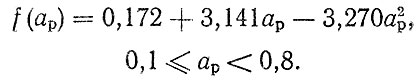(1.15)

Рис. 1.6. Функции распределения нормированных относительно единицы средних ресурсов при расчете: 1 - по линейному варианту гипотезы [формула (1.13)] 1/а; 2 - по корректированному варианту гипотезы, а_р/а; 3 - с корректировкой по формуле (1.16)

Нормированная функция F [a/af(а_р)] с учетом (1.15) приведена на рис. 1.6. С вероятностью Р = 0,95 погрешность расчета по уточненной корректированной гипотезе составляет 170%. Таким образом, формула для расчета среднего (медианного) ресурса деталей шасси автомобиля запишется в виде

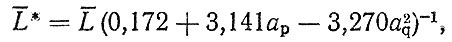(1.16)

где L^- - определяется по формуле (1.13); а_р - по формуле (1.14).

На основе гипотезы суммирования повреждений разработаны методики и даны примеры расчетов на усталостную долговечность следующих деталей автомобиля: зубчатых колес коробок передач и главных передач (на изгиб и контактную усталость); подшипников коробок передач, главных передач, ступиц колес; валов трансмиссии; рессор; карданных шарниров; балок мостов; накладок сцепления; поворотных кулаков. Однако существенным недостатком этих расчетов является то, что за редким исключением их результаты не сопоставлены с фактическими ресурсами и они выполнены на различной информационной базе, т. е. по различным вариантам гипотезы, при различных способах схематизации нагрузочных режимов и в большинстве случаев без учета эксплуатации автомобиля в различных условиях.

Методы расчета на статическую прочность

Из анализа работ, посвященных статической прочности применительно к оценке надежности механических систем [4, 6, 28, 55 и др.], следует, что можно выделить два направления в расчетах: детерминистическое (по коэффициентам запаса n) и вероятностное.

В автомобильной промышленности оценка прочности по коэффициентам запаса широко используется ввиду простоты расчета и возможности экспериментальной проверки, В табл. 1.6 приведены систематизированные данные по расчетно-экспериментальным коэффициентам запаса деталей трансмиссии автомобилей [52, 74]. Из нее видно, что в основном для деталей всех агрегатов n > 1. Коэффициенты запаса используются и при оценке усталостной долговечности, когда спектр нагрузок находится ниже предела выносливости. Существенным недостатком этого метода является невозможность количественного определения показателей надежности, в частности долговечности.

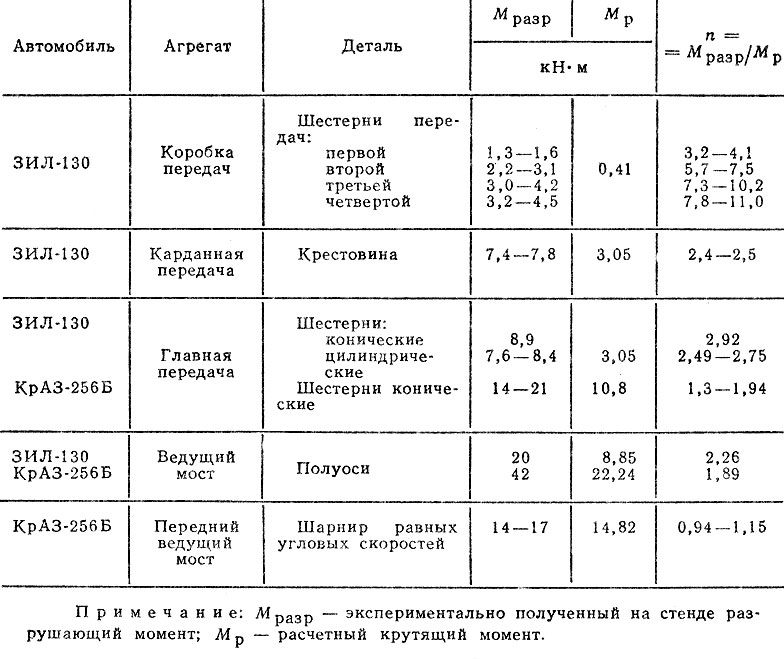
Таблица 1.6. Запасы статической прочности деталей автомобиля

При вероятностном расчете нагрузка S и прочность R представляются как случайные величины (рис. 1.7). Если эти величины независимы, то вероятность безотказной работы (т. е. вероятность не разрушения) определяется из выражения

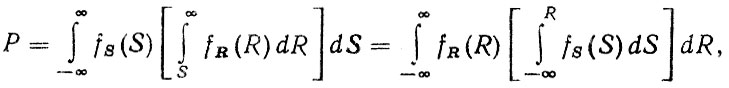(1.17)

где f_s(S) - плотность распределения нагрузки; f_R(R) - плотность распределения прочности (несущей способности).

Модель (1.17) получила название "нагрузка - несущая способность".

Если f_s(S) и f_R(R) подчиняются нормальным законам распределения с параметрами m_R, m_s (средние значения прочности нагрузки) и σ_R, σ_S (средние квадратические отклонения), то вероятность безотказной работы определяется по формуле

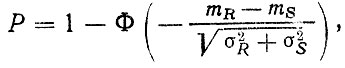(1.18)

где Φ( ) - интеграл вероятностей, значения которого табулированы.

Следует подчеркнуть, что в работах [28, 50 3 приводятся формулы для вероятности безотказной работы Р, когда прочность подчиняется законам распределения для существенно положи-тельных величин экспоненциальному, Рэлея? Вейбулла и др. без параметров сдвига.

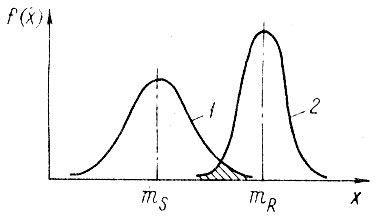
Рис. 1.7. Расчет на статическую прочность: 1 - плотность распределения нагрузки; 2 - плотность распределения прочности

Правильность полученных выражений не вызывает возражений, но они не приемлемы с физической точки зрения, так как ни одна деталь не проектируется с минимальным значением прочности, равным нулю.

Вероятностный подход позволяет оценить безотказность детали и может быть применен при расчете так называемой схемной надежности, но для получения оценок долговечности в плотности распределения нагрузки и (или) прочности должны быть введены временные характеристики. Необходимо обратить внимание на то, что практически отсутствуют исследования по вопросам расчета ресурса деталей при одновременном протекании в них нескольких разрушительных процессов, а также оценки показателей надежности агрегатов, включающих детали, плотности, распределения ресурсов которых получены на основе моделей отказов.